POLYFILL Procedure
Fills the interior of a region of the display enclosed by an arbitrary 2D or 3D polygon.
Usage
POLYFILL, x[, y[, z]]
Input Parameters
x — A vector parameter providing the x-coordinates of the points to be connected.
If only one parameter is specified, x must be an array of either two or three vectors: (2,*) or (3,*). In this special case, x(0,*) is taken as the x values, x(1,*) is taken as the y values, and x(2,*) is taken as the z values.
y — (optional) A vector parameter providing the y-coordinates of the points to be connected.
z — (optional) If present, a vector parameter providing the z-coordinates of the points to be connected. If z is not present, x and y are used to draw lines in two dimensions. z has no effect if the keyword T3d is not specified and the system variable !P.T3d = 0.
Keywords
Keywords let you control many aspects of the plot’s appearance. POLYFILL keywords are listed below. For a description of each keyword, see
Graphics and Plotting Keywords.
Z-buffer Specific Keywords
These keywords allow you to warp images over 2D or 3D polygons; the keywords are valid only when the Z-buffer device is active. For more information on the Z-buffer, see
Output Devices and Window Systems.
Image_Coordinates — To warp an image over a polygon, pass the image into POLYFILL with the Pattern keyword, and specify a (2, n) array containing the image space coordinates that correspond to each of the n vertices with the Image_Coordinates keyword.
Image_Interpolate — When present and nonzero, specifies that bilinear interpolation is used instead of the nearest-neighbor method of sampling.
Mip — When present and nonzero, produces improved transparency by Maximum Intensity Projection. Rather than setting an arbitrary threshold value, a pixel is set in the Z-buffer, regardless of its depth, if its intensity is greater than the current pixel in the buffer.
Threshold — Pixels less than the Threshold value are not drawn, producing a transparent effect.
Discussion
The polygon is defined by a list of connected vertices stored in x, y, and z. The coordinates can be given in data, device, or normalized form using the Data, Device, or Normal keywords.
POLYFILL uses various filling methods:

solid fill

parallel lines

a pattern contained in an array

hardware-dependent fill pattern
Solid Fill Method — Most devices can fill with a solid color. Solid fill is performed using the line fill method for devices that don’t have this hardware capability. Keywords that specify a method are not required for solid filling.
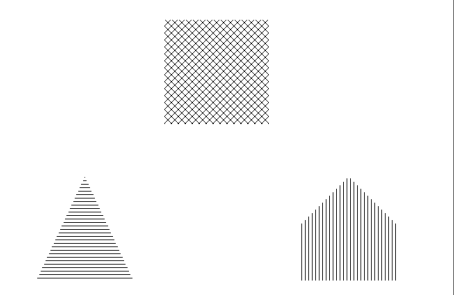
Line Fill Method — Filling using parallel lines is device independent and works on all devices that can draw lines. Cross-hatching may be obtained with multiple fillings of differing orientations. The spacing, linestyle, orientation, and thickness of the filling lines may be specified using the corresponding keywords. The Line_Fill keyword selects this filling style, but is not required if either the Orientation or Spacing keywords are present.
Patterned Fill Method — The method of patterned filling and the usage of various fill patterns is hardware dependent. The fill pattern array may be directly specified with the Pattern keyword for some output devices on UNIX only. If this keyword is omitted, the polygon is filled with the hardware-dependent pattern index specified by the Fill_Pattern keyword.
Example 1 (UNIX only)
In this example, POLYFILL is used to create and fill a square, triangle, and pentagon with different patterns. Device coordinates are used for these polygons. The results are shown in
Figure 13-13: Pattern-filled Polygons on page 921.
a = INTARR(10, 10)
; Create fill pattern for square. This will be an X pattern.
FOR i=0L, 9 DO a(i, i) = 255
a = a + ROTATE(a, 1)
; Create square and fill it with the pattern in variable a.
POLYFILL, [225, 375, 375, 225], $
[275, 275, 425, 425], /Device, Pattern=a
; Create fill pattern (horizontal lines) for triangle.
b = INTARR(10, 10)
b(*, 2) = 255
b(*, 7) = 255
; Create triangle and fill it with the pattern in variable b.
POLYFILL, [40, 180, 110], [50, 50, 200], /Device, Pattern=b
c = INTARR(10, 10)
; Create fill pattern (vertical lines) for pentagon.
c(2, *) = 255
c(7, *) = 255
; Create pentagon and fill it with the pattern in variable c.
POLYFILL, [420, 560, 560, 490, 420], $
[50, 50, 130, 200, 130], /Device, Pattern=c
Example 2
This example uses POLYFILL to draw the faces of cubes that are stacked on top of each other in pyramid fashion. The width and length of the base of the stack is equal to numcubes. This value is an argument passed to the procedure that draws the cubes.
The SURFACE procedure is used to establish a three-dimensional transformation matrix that determines the view. The T3d keyword is used with POLYFILL so that the transformation matrix established by SURFACE is used.
; Draw a cube.
PRO draw_cube, x, y, z
COMMON com1, size, colr1, colr2, colr3
left_face, x, y, z, colr1
right_face, x, y, z, colr2
top_face, x, y, z, colr3
END
PRO left_face, x, y, z, colr
COMMON com1, size
; Use POLYFILL to draw the left face of a cube.
POLYFILL, [x, x, x, x], [y, y, y + size, y + size], $
[z, z - size, z - size, z], /T3d, Color=colr
END
PRO right_face, x, y, z, colr
COMMON com1, size
; Use POLYFILL to draw the right face of a cube.
POLYFILL, [x, x + size, x + size, x], [y, y, y, y], $
[z, z, z - size, z - size], /T3d, Color=colr
END
PRO top_face, x, y, z, colr
COMMON com1, size
; Use POLYFILL to draw the top face of a cube.
POLYFILL, [x, x + size, x + size, x], [y, y, y + size, $
y + size], [z, z, z, z], /T3d, Color=colr
END
; Argument numcubes is number of cubes to place along base.
PRO cubes, numcubes
COMMON com1, size, colr1, colr2, colr3
; Determine size, which is the width, height, and length of
; each cube. Note that everything is normalized to lie between
; 0 and 1.
size = 1.0D/numcubes
; Load red temperature color table.
LOADCT, 3
; Establish three-dimensional transformation using SURFACE.
; The Nodata keyword permits the use of a dummy
; two-dimensional array to be passed to SURFACE. Setting
; XStyle, YStyle, and ZStyle to 4 causes axes to be invisible.
; The ranges are set here, and the transformation is saved.
SURFACE, FLTARR(2, 2), /Nodata, XStyle=4, $
YStyle=4, ZStyle=4, XRange=[0, 1], $
YRange=[-1, 0], ZRange=[0, 1], /Save
; Determine available colors to use.
colr1 = WoColorConvert(FIX(128))
colr2 = WoColorConvert((FIX((256 - colr1)/2.0) + $
colr1) MOD 256)
colr3 = WoColorConvert((FIX((256 - colr2)/2.0) + $
colr1) MOD 256)
z = 0
FOR i = FIX(numcubes), 1, -1 DO BEGIN
x = (FIX(numcubes) - i) * size
y = -size
z = z + size
; Draw the cubes by layer, starting at the bottom.
FOR j=1L, i - 1 DO BEGIN
; Draw cubes along the left edge of the current layer.
draw_cube, x, y, z
y = y - size
ENDFOR
x = (i - 1) * size + x
FOR j=1L, i DO BEGIN
; Draw cubes along the right edge of the current layer.
draw_cube, x, y, z
x = x - size
ENDFOR
ENDFOR
END
If this procedure is contained in a file named cubes.pro in your directory, it can be compiled with the following command:
.RUN cubes
The number of levels in the pyramid height is equal to the number passed to cubes. If the procedure is run with the command:
cubes, 8
then a pyramid with eight levels is created.
See Also
Version 2017.0
Copyright © 2017, Rogue Wave Software, Inc. All Rights Reserved.