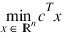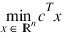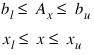LINPROG Function (PV-WAVE Advantage)

IMSL Mathematics Reference Guide > Optimization > LINPROG Function (PV-WAVE Advantage)

Solves a linear programming problem using the revised simplex algorithm.

Usage

result = LINPROG(a, b, c)

Input Parameters

a—Two-dimensional matrix containing the coefficients of the constraints. The coefficient for the ith constraint is contained in A (i, *).

b—One-dimensional matrix containing the right-hand side of the constraints. If there are limits on both sides of the constraints, b contains the lower limit of the constraints.

c—One-dimensional array containing the coefficients of the objective function.

Returned Value

result—The solution x of the linear programming problem.

Input Keywords

Double—If present and nonzero, double precision is used.

Bu—Array with N_ELEMENTS(b) elements containing the upper limit of the constraints that have both the lower and the upper bounds. If no such constraint exists, Bu is not needed.

Irtype—Array with N_ELEMENTS(b) elements indicating the types of general constraints in the matrix A. Let ri = Ai0x0 + ... + Ain–1 xn–1. The value of Irtype (i) is described in Constraint Types.

Table 9-4: Constraint Types
Irtype (i)	Constraints
0	ri = bi
1	ri ≤ bu
2	ri ≥ bi
3	bi ≤ ri ≤ bu

Default: Irtype (*) = 0

Xlb—Array with N_ELEMENTS(c) elements containing the lower bound on the variables. If there is no lower bound on a variable, 1030 should be set as the lower bound. Default: Xlb (*) = 0

Xub—Array with N_ELEMENTS(c) elements containing the upper bound on the variables. If there is no upper bound on a variable, –1030 should be set as the upper bound. Default: Xub (*) = infinity

Itmax—Maximum number of iterations. Default: Itmax = 10,000

Output Keywords

Obj—Name of the variable into which the optimal value of the objective function is stored.

Dual—Name of the variable into which the array with N_ELEMENTS(c) elements, containing the dual solution, is stored.

Discussion

Function LINPROG uses a revised simplex method to solve linear programming problems; i.e., problems of the form:

subject to:

where c is the objective coefficient vector, A is the coefficient matrix, and the vectors bl, bu, xl, and xu are the lower and upper bounds on the constraints and the variables.

For a complete discussion of the revised simplex method, see Murtagh (1981) or Murty (1983). This problem can be solved more efficiently.

Example

The linear programming problem in the standard form:

min f(x) = –x0 – 3x1

subject to:

is solved.

; Define the coefficients of the constraints.

RM, a, 4, 6

1 1 1  0 0 0

1 1 0 -1 0 0

1 0 0  0 1 0

0 1 0  0 0 1

; Define the right-hand side of the constraints.

RM, b, 4, 1

1.5

.5

; Define the coefficients of the objective function.

RM, c, 6, 1

-1

-3

; Call LINPROG and print the solution.

PM, LINPROG(a, b, c), Title = 'Solution'

; PV-WAVE prints the following:

; Solution

; 0.500000

; 1.00000

; 0.00000

; 1.00000

; 0.500000

; 0.00000

Warning Errors

MATH_PROB_UNBOUNDED—Problem is unbounded.

MATH_TOO_MANY_ITN—Maximum number of iterations exceeded.

MATH_PROB_INFEASIBLE—Problem is infeasible.

Fatal Errors

MATH_NUMERIC_DIFFICULTY—Numerical difficulty occurred. If float is currently being used, using double may help.

MATH_BOUNDS_INCONSISTENT—Bounds are inconsistent.

Version 2017.0