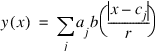RBFIMSCL Procedure (PV-WAVE Advantage)

rbfi—While it is not necessary to understand the rbfi data structure to use RBFIMSCL, it is described here for completeness. rbfi is a list defining an interpolant to the data ydat(xdat): rbfi(0) is a 2-element list containing an n-element vector and an (n,n) array defining an invertible affine transformation of the data coordinates into coordinates more efficient for computation. rbfi(0) is set with keywords but defaults to the identity map. rbfi(1) is an (n+1)-element coefficient vector defining a linear fit to the transformed data: y=total(rbfi(1)*[1,x]). The interpolant is the sum of the linear function and a radial basis function, but unless keyword Line is set, the linear function is simply the n-plane y = 0. rbfi(2) is a structure defining an RBF interpolant to the deviation of a small datasubset from the linear function rbfi(1). If the small datasubset is not the entire dataset and the residual at any datapoint exceeds tolerance, then an rbfi(3) is an RBF interpolant to the residuals evaluated at a datasubset approximately 2n times larger than that of rbfi(2). This process continues with increasing dataset size until the residual at every datapoint meets the accuracy requirement. Each RBF interpolant is of the form:

Eval—If set to any scalar then xdat and rbfi must be input, and ydat is output as values of the interpolant rbfi at points xdat. By default this keyword is not set.

Cent—If set to any scalar then computations are performed in coordinates which represent a translation of the origin to the data centroid. This can improve accuracy if the data is clustered far from the origin. By default this keyword is not set.

Paxs—If set to any scalar then computations are performed in coordinates which represent a translation of the origin to the data centroid, followed by a rotation to the principal axes. This can improve efficiency if the data bounding box is smaller in principal coordinates. By default this keyword is not set.

Cube—If set to any scalar then computations are performed in coordinates which represent a translation of the origin to the data centroid, followed by a rotation to the principal axes, followed by a dilation into the unit hypercube. This can be useful when the independent variables are measured in different units. By default this keyword is not set.

Dstn—Name of a user-supplied distance function or a symmetric positive definite (n,n) array defining a distance metric. If an array is supplied, then computations are performed in coordinates which represent a translation of the origin to the data centroid, followed by a linear transformation to canonical Euclidean coordinates. This is more efficient than directly using the metric to compute distance. If a function is supplied then its input must be a (p,n) array b and a (q,n) array c defining two sets of points in n-space, and its output must be a (p,q) array d where d(i,j) is the distance between b(i,*) and c(j,*). The default distance measure is Euclidean relative to Cartesian coordinates. If a function is supplied then rbfi(0) contains the function name, and Cent, Paxs, and Cube are ignored.

Affi—A 2-element list which directly sets rbfi(0), overriding any settings from Cent, Paxs, Cube, or Dstn. New coordinates should be defined as xnew = rbfi(0,1) # (xold – rbfi(0,0)).

Line—If set to any scalar then the interpolant is the sum of a linear function and a radial basis function which interpolates the nonlinear component of the data, otherwise the linear term is simply the n-plane y = 0. By default this keyword is not set.

Crbf—Name of a user-supplied basis function: RBFIMSCL sends the basis function an array of values in the range [0,1]. The basis function returns an array of the same size representing a decreasing continuous function [0,1,infinity] -> [1,0,0]. The default basis function is the unique (Wendland) polynomial of minimal degree which yields a C2 interpolant and a positive definite linear system of equations for the RBF coefficients. Besides the default basis function, a second pre-written basis function can be accessed by setting Crbf='wendndc0'; this one is the Wendland polynomial which yields a C0 interpolant. The default basis function works well for smoothly varying data, but for sharply changing data, the C0 basis function may be desireable. For interpolant differentiability C4 and higher, a suitable Wendland polynomial basis function is easily constructed with the WENDCOEF Function (PV-WAVE Advantage) and POLYEVAL Function (PV-WAVE Advantage).

Nsz0—An integer which determines the rbfi(2) (irregular) grid of centers. By default centers are spaced as evenly as possible on the data bounding box, initially with Nsz0 = 2 centers along shortest dimension and with the number along any other dimension increased in proportion to dimension length. Nsz0 affects convergence properties and the shape of the interpolant (or extrapolant) in large regions void of data. The small default provides the most robust convergence properties and provides nice smoothing from small gradients into large regions void of data. Larger values suppress this effect, which may be desirable for void regions bounded by large gradients, but too large a value impedes convergence.

Itmx—(I/O) Maximum number of iterations. The default is 1E5. On input, Itmx is a limit on the number of conjugate gradient iterations that can be accumulated over all greedy iterations on the set of centers. If Itmx is exceeded then processing stops and the current approximation to the interpolant is returned. On output, Itmx contains the number of accumulated iterations.

Rtol—(I/O) Scalar accuracy requirement for the solution: The interpolant must not deviate from any datapoint by more than Rtol*max(abs(y)) where y is the dependent variable input (ydat) after subtraction of any linear term. On output, Rtol is the accuracy achieved. The default is 1E–3. For large datasets, slightly larger Rtol values, for example 2E–3, can sometimes result in a dramatic reduction in computation time or memory requirements.

Fnam—The name of a scratch file. Defaults to rbfintrp.temp. For large datasets it is more efficient if Fnam refers to a file on a local disk. By default the scratch file is written to the PV-WAVE home directory. If this directory is on a disk remote from the machine running PV-WAVE and Fnam is not used, then scratch file I/O can be very time consuming for large datasets. In a situation like this, it is very important that Fnam be given the full path to some file on a disk local to the machine running PV-WAVE. Two instances of RBFIMSCL cannot simultaneously use the same scratch file, so unique values of Fnam should be ensured if the possibility of such a conflict exists. RBFIMSCL creates the scratch file only in fitting mode (not in evaluation mode) and on exit its contents are erased, but the 0 byte file is not deleted.

Smul—Scalar multiple of the default support radius. For each level of the interpolant, the default support radius is approximately twice the maximum distance from any center to its nearest neighbor. The default is Smul = 1. Larger values increase computational effort but do not appreciably change the shape of the interpolant except in large regions void of data. Smaller values reduce computation and can sometimes produce a good interpolant anyway, especially in well-sampled or high-dimensional datasets.

Tdim—Positive integer indicating the data domain topological dimension. For example data sampled on a circle in a plane has topological dimension 1 and space dimension 2. Tdim defaults to the space dimension n, but if the domain topological dimension is less than n then setting Tdim can make the algorithm faster provided that the data sampling density is high enough to support the assertion of Tdim.

Nonu—If set, the algorithm more efficiently accommodates a big distribution which is highly nonuniform on its domain. Nonu defaults to 'off' and should be used only if the data set is large and if its distribution is highly nonuniform.

Ydaj—If Eval is set then Ydaj is a list of m-element vectors representing the converging sequence of interpolants to the data.

RBFIMSCL fits interpolants to data sets of general size, dimensionality, structure, and complexity. It computes a meshless interpolant which is an analytically differentiable function, and it can evaluate the interpolant at any specified point set. While sampling the data at increasing scales of resolution, RBFIMSCL generates a converging sequence of interpolants built from compactly supported radial basis functions (see rbfi parameter description above). This RBF algorithm admits problems many times larger than those admitted by RADBF. A scratch file, rbfintrp.temp, is created and deleted as necessary, and it can be very large for complex, multi-dimensional data sets (refer to the Fnam keyword).

In this example we create 400 points randomly located on the top half of the unit sphere and use RBFIMSCL to build an interpolating function to the data. Then we use RBFIMSCL to evaluate the function on a 101 by 101 grid and display the resulting surface along with the original data.

An extensive suite of interactive examples are available in <RW_DIR>/wave/lib/user/examples/

Examples are in four procedures rbfimscl_exn.pro for n=1,2,3,4; one procedure for each data space dimension. Each procedure allows data to be input directly or to be randomly generated with keywords that provide a great deal of control over its spatial distribution. Each procedure uses RBFIMSCL to generate an interpolant to the data and then to evaluate the interpolant at user-specified points or on a n-dimensional grid whose size is controlled by a keyword. If the interpolating function is evaluated on a grid then it is displayed along with the data by default, although a keyword allows various aspects of the display to be supressed. The display method depends on space dimension: line-plots for 1D data, VTK surfaces for 2D data, VTK isosurfaces for 3D data, and 2-dimensional image-slices for 4D data. Each procedure provides a keyword interface to each RBFIMSCL keyword so the user can compare the effects of different keywords; the interpolating function and its evaluations can be returned as output parameters so these comparisons can be made numerically as well as visually.

Any random test data is built with a generating function which is the sum of a N-variate polynomial and an ND Fourier series. The polynomial and series coefficients can be input directly or any number of them can be randomly generated. The specified number of datapoints are then random evaluations of the generating function. The evaluation locations can be confined to an eccentric ND annulus whose inner and outer centers, radii, and shapes are user-specified. All of this flexibility is provided so that the user can easily simulate semi-realistic data sampled on irregular ND domains and evaluated with varying degrees of functional complexity.