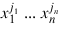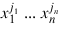POLYEVAL Function (PV-WAVE Advantage)
Evaluates a polynomial in n variables.
Usage
y = POLYEVAL ( p, x)
Input Parameters
p—n-dimensional array of polynomial coefficients: p(j1, ..., jn) is the coefficient for:
where the xi are the indeterminants of the polynomial.
x—(m,n) array of m points at which to evaluate the polynomial.
Returned Value
y—m-element vector containing the value of the polynomial at each of the m input points.
Keywords
Form—If set and n=1 then x need not be 1-dimensional but instead can have any desired dimensionality, and output y has the same dimensions as x. Also, setting Form invokes a faster algorithm specific to the case n=1.
Discussion
POLYEVAL evaluates a n-variate polynomial which is defined by an n-dimensional array of coefficients. The coefficients usually represent a regression model obtained by POLYFITN.
Example 1
; make 10 points in 3-space and store the range of the data
seed = 0
data = [ [RANDOMU(seed,10,2)], [RANDOMU(seed,10)/10] ]
drng = [ MIN(data,Dimension=0,Max=dmax), dmax ]
; coefficients of an exact bivariate 3rd order polynomial fit
MATH_INIT
coef = POLYFITN(data, [[1,1,1,1],[1,1,1,0],[1,1,0,0],[1,0,0,0]])
; grid of points that spans the range of the 2 independent
; variables
axes = LIST( INTERPOL(drng(*,0),101), INTERPOL(drng(*,1),101) )
grid = CPROD(axes)
; evaluate the polynomial on the grid; display the surface and
; data
surf = POLYEVAL( coef, grid )
vtkWINDOW, /Norender
vtkSURFACE, REFORM(surf,101,101), axes(0), axes(1)
vtkSCATTER, TRANSPOSE(data), Color=255L, Scale=0.2, /Noerase, $
/ Noaxes
vtkRENDERWINDOW
Example 2
See wave/lib/user/examples/polyexam.
This routine displays a univariate polynomial fit to random data, a bivariate polynomial fit to random data, and an image warping accomplished with a bivariate polynomial fit to each of two image coordinate mappings.
Version 2017.0
Copyright © 2017, Rogue Wave Software, Inc. All Rights Reserved.