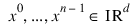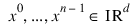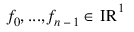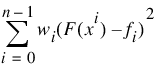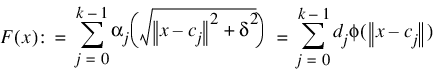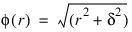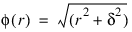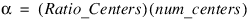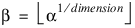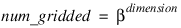RADBF Function (PV-WAVE Advantage)
Computes an approximation to scattered data in Rn for n ≥ 2 using radial-basis functions.
Usage
result = RADBF(abscissa, fdata, num_centers)
Input Parameters
abscissa—Two-dimensional array containing the abscissas of the data points. Parameter abscissa (i, j) is the abscissa value of the j‑th data point in the ith dimension.
fdata—One-dimensional array containing the ordinates for the problem.
num_centers—Number of centers to be used when computing the radial-basis fit. Parameter num_centers should be less than or equal to N_ELEMENTS (fdata).
Returned Value
result—A structure that represents the radial-basis fit.
Input Keywords
Centers—User-supplied centers. See Discussion below for details.
Double—If present and nonzero, double precision is used.
Ratio_Centers—Desired ratio of centers placed on an evenly spaced grid to the total number of centers. There is a condition: The same number of centers placed on a grid for each dimension must be equal. Thus, the actual number of centers placed on a grid is usually less than Ratio_Centers * num_centers, but is never more than Ratio_Centers * num_centers. The remaining centers are randomly chosen from the set of abscissa given in abscissa. Default: Ratio_Centers = 0.5
Random_Seed—Value of the random seed used when determining the random subset of abscissa to use as centers. By changing the value of seed on different calls to RADBF, with the same data set, a different set of random centers are chosen. Setting Random_Seed to zero forces the random number seed to be based on the system clock, so possibly, a different set of centers is chosen each time the program is executed. Default: Random_Seed = 234579
Basis—Character string specifying a user-supplied function to compute the values of the radial functions. The form of the input function is ϕ (r). Default: the Hardy multiquadratic
Delta—Delta used in the default basis function, φ (r) = SQRT(r2 + δ2). Default: Delta = 1
Weights—Requires the user to provide the weights. Default: all weights equal 1
Discussion
Function RADBF computes a least-squares fit to scattered data in Rd. More precisely, let n = N_ELEMENTS (fdata), x = abscissa, f = fdata, and d = N_ELEMENTS (abscissa (0, *)). Then:
This function computes a function F which approximates the above data in the sense that it minimizes the sum-of-squares error:
where w = Weights.
The functional form of F is, of course, restricted as follows:
The function φ is called the radial function. It maps R1 into R1. It needs to be defined only for the nonnegative reals. For the purpose of this routine, the user supplied a function:
Note that the value of delta is defaulted to 1. It can be set by the user by using keyword Delta.
The default-basis function is the Hardy multiquadric and is defined as:
A key feature of this routine is the user’s control over the selection of the basis function.
In order to obtain the default selection of centers, first compute the number of centers that will be on a grid and the number that will be on a random subset of the abscissa. Next, compute those centers on a grid. Finally, a random subset of abscissa is obtained. This determines where the centers are placed. The selection of centers is discussed in more detail below.
First, the computed grid is restricted to have the same number of grid values in each of the “dimension” directions. Then, the number of centers placed on a grid, num_gridded, is computed as follows:
Note that β grid values are in each of the “dimension” directions. Then:
num_random = (num_centers) – (num_gridded)
How many centers are placed on a grid and how many are placed on a random subset of the abscissa is now known. The gridded centers are computed such that they are equally spaced in each of the “dimension” directions. The last problem is to compute a random subset, without replacement, of the abscissa. The selection is based on a random seed. The default seed is 234579. The user can change this using optional argument Random_Seed. Once the subset is computed, the abscissa as centers is used.
Since the selection of good centers for a specific problem is an unsolved problem at this time, ultimate flexibility is given to the user; that is, the user can select centers using keyword Centers. As a rule of thumb, the centers should be interspersed with the abscissa.
The return value for this function is a pointer to the structure containing all the information necessary to evaluate the fit. This pointer is then passed to function RADBE to produce values of the fitted function.
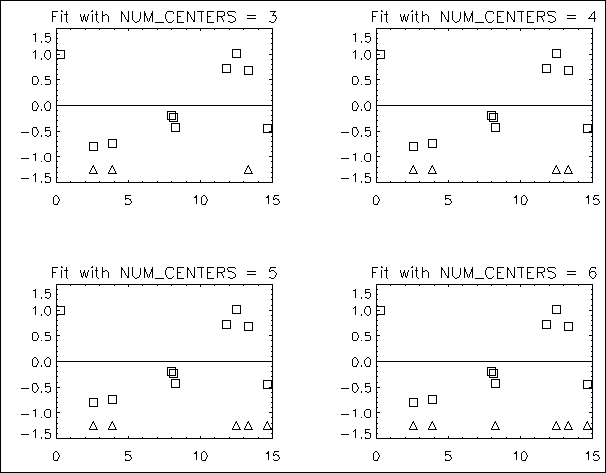
Example 1: Fitting Noisy Data with Default Radial Function
In this example, RADBF is used to fit noisy data. Four plots are generated using different values for
num_centers as shown in
Figure 4-17: Fits using Differential Values for Num_centers on page 190. The plots generated by running this example are included after the code. Note that the triangles represent the placement of the centers.
PRO radbf_ex1
!P.Multi = [0, 2, 2]
ndata = 10
noise_size = .05
; Set up parameters.
xydata = DBLARR(1, ndata)
fdata = DBLARR(ndata)
; Set the random number seed.
RANDOMOPT, Set = 234579
; Generate the noisy data.
noise = 1 - 2 * RANDOM(ndata, /Double)
xydata(0, *) = 15 * RANDOM(ndata)
fdata = REFORM(COS(xydata(0, *)) + noise_size * noise, ndata)
FOR i=0L, 3 DO BEGIN
; Loop on different values of num_centers.
num_centers = ndata/3 + i
; Compute the fit.
radial_struct = RADBF(xydata, fdata, num_centers)
a = DBLARR(1, 100)
a(0, *) = 15 * FINDGEN(100)/99.
; Evaluate fit.
fit = RADBE(a, radial_struct)
title = 'Fit with NUM_CENTERS = ' + $
STRCOMPRESS(num_centers, /Remove_All)
; Plot results.
PLOT, xydata(0, *), fdata, Title = title, $
Psym = 6, Yrange = [-1.25, 1.25]
; Plot the original data as squares.
OPLOT, a(0, *), fit
; Plot the x-values of the centers as triangles.
OPLOT, radial_struct.CENTERS, $
MAKE_ARRAY(num_centers, Value=-1.25), Psym = 5
END
END
Example 2: Fitting Noisy Data with User-supplied Radial Function
This example fits the same data as the first example, but the user supplies the radial function and sets
Ratio_Centers to zero. The radial function used in this example is
φ (
r) =
ln (1 +
r2). Four plots are generated using different values for
num_centers as shown in
Figure 4-18: Fit using a User-Defined Radial Function on page 192. The plots generated by running this example are included after the code. Note that the triangles represent the placement of the centers.
; Define the radial function.
FUNCTION user_fcn, distance
RETURN, ALOG(1 + distance^2)
END
PRO radbf_ex2
; Set up parameters.
!P.Multi = [0, 2, 2]
ndata = 10
noise_size = .05
xydata = DBLARR(1, ndata)
fdata = DBLARR(ndata)
; Set the random number seed.
RANDOMOPT, Set = 234579
; Generate the noisy data.
noise = 1 - 2 * RANDOM(ndata, /Double)
xydata(0, *) = 15 * RANDOM(ndata)
fdata = REFORM(COS(xydata(0,*)) + noise_size * noise, ndata)
FOR i=0L, 3 DO BEGIN
; Loop on different values of num_centers.
num_centers = ndata/3 + i
; Compute the fit.
radial_struct = RADBF(xydata, fdata, $
num_centers, Ratio_Centers = 0, Basis = 'user_fcn')
a = DBLARR(1, 100)
a(0, *) = 15 * FINDGEN(100)/99.
; Evaluate fit.
fit = RADBE(a, radial_struct)
title = 'Fit with NUM_CENTERS = ' + $
STRCOMPRESS(num_centers, /Remove_All)
; Plot results.
PLOT, xydata(0,*), fdata, Title = title, $
Psym = 6, Yrange = [-1.25, 1.25]
OPLOT, a(0, *), fit
OPLOT, radial_struct.CENTERS, $
MAKE_ARRAY(num_centers,Value = -1.25), Psym = 5
END
END
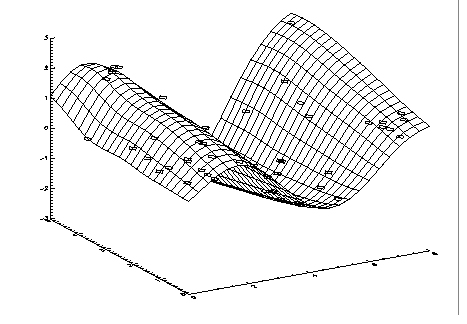
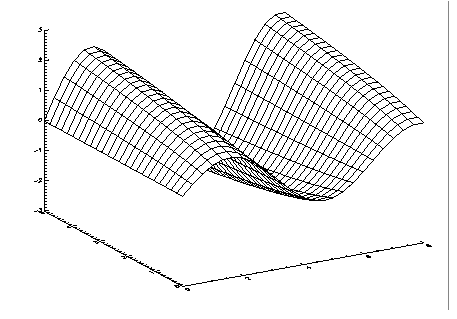
Example 3: Fitting a Surface to Three-dimensional Scattered Data
This example fits a surface to scattered data. The scattered data is generated using the function
f (
x, y) =
exp (ln (
y + 1) sin (
x)). The plots generated by running this example are included after the code as shown in
Figure 4-19: Surface Fit to Scatttered Data on page 194 and
Figure 4-20: Function used to Generate Scattered Data on page 195.
; This function generates the scattered data function values.
FUNCTION f, x1, x2
RETURN, EXP(ALOG10(x2 + 1)) * SIN(x1)
END
PRO radbf_ex3
; Set up initial parameters.
RANDOMOPT, Set = 123457
ndata = 50
num_centers = ndata
xydata = DBLARR(2, ndata)
fdata = DBLARR(ndata)
xrange = 8
yrange = 5
; Generate data.
xydata(0,*) = xrange * RANDOM(ndata, /Double)
xydata(1,*) = yrange * RANDOM(ndata, /Double)
fdata(*) = f(xydata(0, *), xydata(1, *))
; Compute fit using RADBF.
radial_struct = RADBF(xydata, fdata, num_centers, Ratio=0)
; Plot results.
WINDOW, /Free
; Variables nx and ny are coarseness of the plotted surfaces.
nx = 25
ny = 25
xyfit = DBLARR(2, nx * ny)
xyfit(0, *) = xrange * (FINDGEN(nx * ny)/ny)/(nx - 1)
xyfit(1, *) = yrange * (FINDGEN(nx * ny) MOD ny)/(ny - 1)
; Use TRANSPOSE and REFORM in order to get the results
; into a form that SURFACE can use.
zfit = TRANSPOSE(REFORM(RADBE(xyfit, Radial_Struct), ny, nx))
xt = xrange * FINDGEN(nx)/(nx-1)
yt = yrange * FINDGEN(ny)/(ny-1)
SURFACE, zfit, xt, yt, /Save, Zrange = [MIN(zfit), MAX(zfit)]
; Plot the original data points over the surface plot.
PLOTS, xydata(0, *), xydata(1, *), fdata, $
/T3d, Psym = 4, Symsize = 2
WINDOW, /Free
orig = DBLARR(nx, ny)
FOR i=0L, (nx-1) DO FOR j=0L, (ny-1) DO $
orig(i, j) = f(xt(i), yt(j))
; Plot original function.
SURFACE, orig, xt, yt, Zrange = [MIN(zfit), MAX(zfit)]
END
Version 2017.0
Copyright © 2017, Rogue Wave Software, Inc. All Rights Reserved.