WgSplineTool Procedure (PV-WAVE Advantage)

Graphical User Interface (GUI) that computes a one-dimensional, least-squares spline fit to (possibly noisy) data.

parent—Widget handle of a parent widget. If supplied, it will be used as the parent shell for the tool.

fit—Structure containing the computed spline. See the introduction of this chapter for a complete description of the spline structure.

shell—Used to pass the shell widget handle for the tool back to the caller.

XData—One-dimensional array containing the abscissas of the data to be fit. If XData is specified, then YData must also be specified.

YData—One-dimensional array containing ordinates of the data to be fit.

XSize—Width, in pixels, of the draw widget used to display the fit. Keyword XSize must be between 100 and 800. Default: XSize = 600

YSize—Height, in pixels, of the draw widget used to display the fit. Keyword YSize must be between 100 and 800. Default: YSize = 600

Demo_Data—If present and nonzero, sets path to the PV‑WAVE example data directory for importing data. Otherwise, WwFileSelection prompts for input from the same directory from which WgSplineTool was invoked.

Foreground—Specifies the default foreground color name.

Background—Specifies the default background color name.

Font—Specifies the name of the default font used for text.

Position—Specifies the position of the upper-left corner of the main window on the screen.

Title—String specifying shell title. Default is “Constrained Spline Tool.”

Procedure WgSplineTool is designed to help compute a least-squares spline fit to (possibly noisy) data. The WgSplineTool procedure computes the fit using function CONLSQ. The default use of WgSplineTool does not require any arguments or keywords and can be used as follows:

There are two ways to supply data to WgSplineTool. First, if the data is contained in variables, for example, x and y, invoke WgSplineTool with the following call:

The variables x and y should be one-dimensional arrays of equal length.

The YData keyword can be used without the XData keyword. in this case, it is assumed that the associated x values are monotonically increasing from 0. The call would be as follows:

The variable y should be a one-dimensional array.

The second method to import data into the application is through an external ASCII file, along with the button labeled Open. The structure of the file is as follows:

For example, the following six lines could be put into a file for use by WgSplineTool:

Once the data has been imported to the application, the data is automatically fitted with the default choice of knots. After this is accomplished, you have the ability to add the order of the fit, the spline space dimension, and the placement of the knots. To adjust the placement of the knots, simply use the mouse to “click and drag” the knots on the plot (the knot abscissae are the triangles that appear near the bottom of the plot). WgSplineTool returns the last computed fit in the argument fit.

Use the Save Spline button to save any intermediate fits. After saving the fit, you can restore the spline at a later time into a variable using the following command:

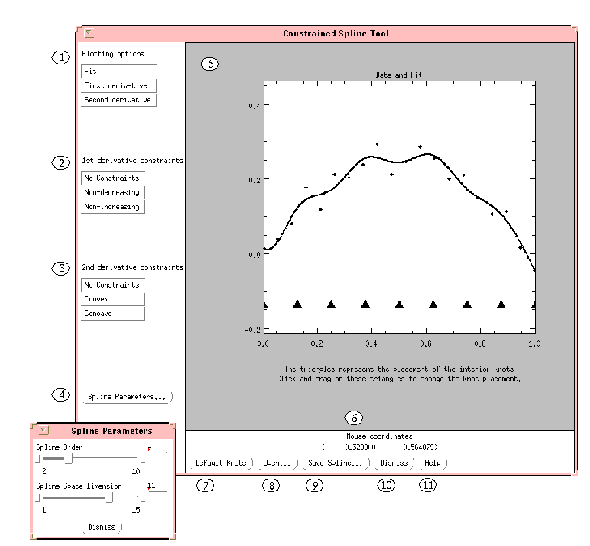
A description of each element of the top-level widget follows. The numbers correspond to the labels in Figure 4-15: Spline Fitting Widget on page 175:

2. 1st Derivative Constraints: Once a fit has been computed, the following choices for global constraints on the first derivative of the computed fit can be enforced:

Forces the fit to be nondecreasing, i.e., the first derivative is non-negative throughout the domain of the data.

Forces the fit to be nonincreasing, i.e., the first derivative is nonpositive throughout the domain of the data.

3. 2nd Derivative Constraints: Once a fit has been computed, the following choices for global constraints on the second derivative of the computed fit can be enforced:

Forces the fit to be convex, i.e., the second derivative is non-negative throughout the domain of the data.

Forces the fit to be concave, i.e., the second derivative is nonpositive throughout the domain of the data.

4. Spline Parameters: Once a fit has been computed, the following spline parameters can be changed using sliders:

5. Plot Window: Displays a plot of the fit in this draw widget. Using the mouse, the knots can be moved from within this window.

6. Mouse Coordinates: As the mouse is moved over the plot, reflects the mouse coordinates. The coordinates are computed in data coordinates.