SPVALUE Function (PV-WAVE Advantage)

IMSL Mathematics Reference Guide > Interpolation and Approximation > SPVALUE Function (PV-WAVE Advantage)

Computes values of a spline or values of one of its derivatives.

Usage

result = SPVALUE(x, spline)

result = SPVALUE(x, y, spline)

Input Parameters

If evaluation of a one-dimensional spline is desired, then arguments x and spline are required. If evaluation of a two-dimensional spline is desired, then x, y, and spline are required.

x—Scalar value or an array of values at which the spline is to be evaluated in the x-direction. If x is an array, then x must be strictly increasing, i.e., x(i) < x(i + 1) for i = 0, (N_ELEMENTS (x) – 2).

y—Scalar value or an array of values at which the spline is to be evaluated in the y-direction. This argument should only be used if spline is a two-dimensional, tensor-product spline. If y is an array, then x must be strictly increasing, i.e., y(i) < y(i + 1) for i = 0, (N_ELEMENTS (y) – 2).

spline—Structure that represents the spline.

Returned Value

result—The values of a spline or one of its derivatives.

Input Keywords

XDeriv—Let XDeriv = p , and let s be the spline that is represented by spline. If s is a one-dimensional spline, this keyword produces the p-th derivative of s at x, s(p) (x). If s is a two-dimensional spline, this keyword specifies the order of the partial derivative in the x-direction. Let q = YDeriv, which has a default value of 0. Then, SPVALUE produces the (p, q)-th derivative of s at (x, y), s(p, q)(x, y). Default: XDeriv = 0

YDeriv—If s = spline is a two-dimensional spline, this keyword specifies the order of the partial derivative in the y-direction. Let p = XDeriv, which has a default value of zero, and q = YDeriv. Then, SPVALUE produces the (p, q)-th derivative of s at (x, y), s(p, q)(x, y). If spline is a one-dimensional spline, this keyword has no effect on computations. Default: YDeriv = 0

Discussion

Function SPVALUE can be used to evaluate splines of the following type:

Piecewise polynomials returned by CSINTERP, CSSHAPE, and CSSMOOTH.

One-dimensional B-splines returned by BSINTERP, BSLSQ, and CONLSQ.

Two-dimensional, tensor-product B-splines returned from BSINTERP and BSLSQ.

If spline is a piecewise polynomial, function SPVALUE computes the values of a cubic spline or one of its derivatives. In this case, the user is required to supply the arguments x and spline and must not supply the argument y. If x is a scalar, then a scalar is returned. If x is a one-dimensional array, then a one-dimensional array of values is returned.The first and last pieces of the cubic spline are extrapolated so that the cubic spline structures returned by the cubic spline routines are defined and can be evaluated on the entire real line. This ability is based on the routine PPVALU by de Boor (1978, p. 89).

If spline is a one-dimensional B-spline, the SPVALUE function computes the values of a spline or one of its derivatives. In this case, the user is required to supply the arguments x and spline and must not supply the argument y. If x is a scalar, then a scalar is returned. If x is a one-dimensional array, then a one-dimensional array of values is returned. This ability is based on the routine BVALUE by de Boor (1978, p. 144).

If spline is a two-dimensional, tensor-product B-spline, the SPVALUE function computes the values of a tensor-product spline or one of its derivatives. In this case, the user is required to supply the arguments x, y, and spline. If x and y are both scalars, then a scalar is returned. If x and y are both one-dimensional arrays, then a two-dimensional array of values is returned, where the (i, j)-th element of the returned matrix is the desired value of SPLINE (x (i), y (j)). This ability is based on the discussion in de Boor (1978, pp. 351–353).

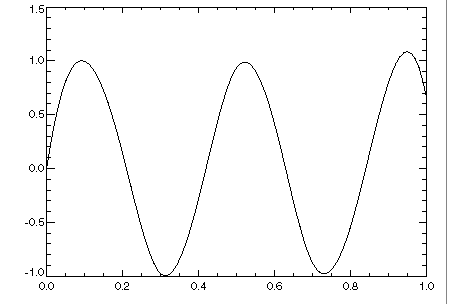
Example 1

In this example, a cubic spline interpolant to function values is computed. The spline is then evaluated, and the results are plotted as shown in Spline Evaluation Plot. Since the default settings are used, the interpolant is determined by the not-a-knot condition (see de Boor 1978).

x = FINDGEN(10)/9

f = SIN(15 * x)

pp = CSINTERP(x, f)

x2 = FINDGEN(100)/99

ppeval = SPVALUE(x2, pp)

PLOT, x2, ppeval

Figure 4-8: Spline Evaluation Plot

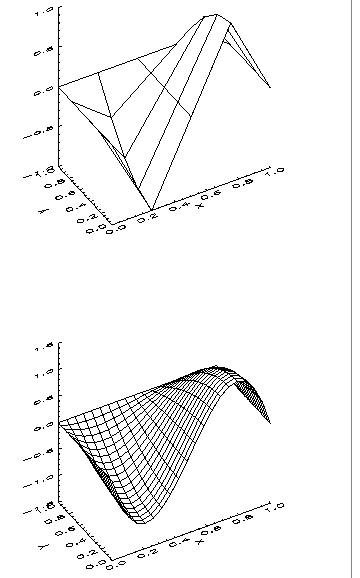
Example 2

This example computes a two-dimensional, tensor-product B-spline using
BSINTERP, then uses SPVALUE to evaluate the spline on a grid, and plots the results as shown in Two-Dimensional Spline Plot Evaluation.

; Generate the data.

x = FINDGEN(5)/4

y = FINDGEN(5)/4

f = FLTARR(5, 5)

FOR i=0L, 4 DO f(i,*) = SIN(2 * !Pi * x(i)) * (-COS(!Pi*y/2))

; Compute the spline by calling BSINTERP.

bs = BSINTERP(x, y, f)

bsval = FLTARR(20, 20)

; Evaluate the spline on a grid.

FOR i=0L, 19 DO BSVAL(i, *) = SPVALUE(i/19., FINDGEN(20)/19, bs)

; Plot the original data and the evaluations of the spline in the

; same plot window.

!P.Multi = [0, 1, 2]

WINDOW, XSize = 400, YSize = 800

; The angle of rotation about x-axis in plots is defined by ax.

ax = 50

!P.Charsize = 1.5

SURFACE, f, x, y, Ax = ax, XTitle = 'X', YTitle = 'Y'

SURFACE, bsval, FINDGEN(20)/19, FINDGEN(20)/19, Ax = ax, $

   XTitle = 'X', YTitle = 'Y'

Figure 4-9: Two-Dimensional Spline Plot Evaluation

Warning Errors

MATH_X_NOT_WITHIN_KNOTS—Value of x does not lie within the knot sequence.

MATH_Y_NOT_WITHIN_KNOTS—Value of y does not lie within the knot sequence.

Fatal Errors

MATH_KNOT_MULTIPLICITY—Multiplicity of the knots cannot exceed the order of the spline.

MATH_KNOT_NOT_INCREASING—Knots must be nondecreasing.

Version 2017.0