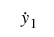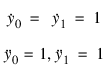ODE Function (PV-WAVE Advantage)
Solves an initial value problem, which is possibly stiff, using the Adams-Gear methods for ordinary differential equations. Using keywords, the Runge-Kutta-Verner fifth-order and sixth-order method can be used if the problem is known not to be stiff.
Usage
result = ODE(t, y, f)
Input Parameters
t—One-dimensional array containing values of the independent variable. Parameter t (0) should contain the initial independent variable value, and the remaining elements of t should be filled with values of the independent variable at which a solution is desired.
y—Array containing the initial values of the dependent variables.
f—Scalar string specifying a user-supplied function to evaluate the right-hand side. This function takes two parameters, t and y, where t is the current value of the independent variable and y is defined above.
The return value of this function is an array defined by the following equation:
Returned Value
result—A two-dimensional array containing the approximate solutions for each specified value of the independent variable. The elements (i, *) are the solutions for the ith variable.
Input Keywords
Double—If present and nonzero, double precision is used.
Tolerance—Scalar value used to set the tolerance for error control. An attempt is made to control the norm of the local error such that the global error is proportional to Tolerance. Default: Tolerance = 0.001
Hinit—Scalar value used for the initial value for the step size h. Steps are applied in the direction of integration. Default: Hinit = 0.001 |t(i + 1) – t(i)|
Hmin—Scalar value used as the minimum value for the step size h. Default: Hmin = 0.0
Hmax—Scalar value used as the maximum value for the step size h. If keyword R_K_V is set, Hmax = 2.0 is used. Default: largest machine-representable number
Max_Steps—Integer value used in the maximum number of steps allowed per time step. Default: Max_Steps = 500
Max_Evals—Integer value used in the maximum number of function evaluations allowed per time step. Default: Max_Evals = no enforced limit
Scale—Scalar value used as a measure of the scale of the problem, such as an approximation to the Jacobian along the trajectory. Default: Scale = 1
Norm—Switch determining the error norm. In the following, ei is the absolute value of the error estimate for yi.

0—Minimum of the absolute error and the relative error equals the maximum of
ei/max ( |
yi|, 1) for
i = 0, ..., N_ELEMENTS (
y) – 1.

1—Absolute error, equals max
iei.

2—The error norm is max
i(
ei/
wi), where
wi = max ( |
yi|,
Floor).

Default:
Norm = 0.
Floor—Used with Norm. Provides a positive lower bound for the error norm option with value 2. Default: Floor = 1.0
R_K_V—If present and nonzero, uses the Runge-Kutta-Verner fifth-order and sixth-order method.
Adams Gear (Default) Method Only
Jacobian—Scalar string specifying a user-supplied function to evaluate the Jacobian matrix. This function takes three parameters, x, y, and yprime, where x and y are defined in the description of the user-supplied function f of the Input Parameters section and yprime is the array returned by the user-supplied function f. The return value of this function is a two-dimensional array containing the partial derivatives. Each derivative ∂y'i / ∂yj is evaluated at the provided (x, y) values and is returned in array location (i, j).
Method—Chooses the class of integration methods:

1—Uses implicit Adams method.

2—Uses backward differentiation formula (BDF) methods.

Default:
Method = 2.
Max_Ord—Defines the highest order formula of implicit Adams type or BDF type to use. Default: value 12 for Adams formulas; value 5 for BDF formulas
Miter—Chooses the method for solving the formula equations:

1—Uses function iteration or successive substitution.

2—Uses chord or modified Newton method and a user-supplied Jacobian matrix.

3—Same as 2 except Jacobian is approximated within the function by divided differences.

Default:
Miter = 3.
Output Keywords
N_Step—Named variable into which the array containing the number of steps taken at each value of t is stored.
N_Evals—Named variable into which the array containing the number of function evaluations used at each value of t is stored.
Adams Gear (Default) Method Only
N_Jevals—Named variable into which the array containing the number of Jacobian function evaluations used at each value of t is stored. The values returned are nonzero only if the keyword Jacobian is also used.
Discussion
Function ODE finds an approximation to the solution of a system of first-order differential equations of the form:
with given initial conditions for y at the starting value for t. The function attempts to keep the global error proportional to a user-specified tolerance. The proportionality depends on the differential equation and the range of integration.
The function returns a two-dimensional array with the (i, j)-th component containing the ith approximate solution at the jth time step. Thus, the returned matrix has dimension (N_ELEMENTS (y), N_ELEMENTS (t)). It is important to notice here that the initial values of the problem also are included in this two-dimensional matrix.
The code is based on using backward differentiation formulas not exceeding order five as outlined in Gear (1971) and implemented by Hindmarsh (1974). There is an optional use of the code that employs implicit Adams formulas. This use is intended for nonstiff problems with expensive functions y' = f(t, y).
If keyword R_K_V is set, the function ODE uses the Runge-Kutta-Verner fifth-order and sixth-order method and is efficient for nonstiff systems where the evaluations of f(t, y) are not expensive. The code is based on an algorithm designed by Hull et al. (1976) and Jackson et al. (1978) and uses Runge-Kutta formulas of order five and six developed by J.H. Verner.
Example 1
This is a mildly stiff example problem (F2) from the test set of Enright and Pryce (1987).
y'0 = – y0 – y0y1 + k0y1
y'1 = –k1y1 + k2 (1 – y1) y0
y0(0) = 1
y1(0) = 0
k0 = 294.
k1 = 3.
k2 = 0.01020408
.RUN
; Define function f.
FUNCTION f, t, y
RETURN, [-y(0) - y(0) * y(1) + 294. * y(1), $
-3.*y(1) + 0.01020408*(1. - y(1)) * y(0)]
END
; Call the ODE code with the values of the independent variable at
; which a solution is desired and the initial conditions.
yp = ODE([0, 120, 240], [1, 0], 'f')
; Output results.
PM, yp, Format = '(3f10.6)', $
Title = ' y(0) y(120) y(240)'
; Results in the following output:
; y(0) y(120) y(240)
; 1.000000 0.514591 0.392082
; 0.000000 0.001749 0.001333
Now solve the same problem but with a user supplied Jacobian. Simply .RUN the following code:
FUNCTION f, t, y
RETURN, [-y(0)-y(0)*y(1)+294.0*y(1), $
-3.0*y(1)+0.01020408*(1.0-y(1))*y(0)]
END
FUNCTION jacob, x, y, dydx
dydx = [ [-y(1)-1,0.01020408*(1-y(1))], $
[294-y(0),-0.01020408*y(0)-3] ]
RETURN, dydx
END
MATH_INIT
yp = ODE( [0,120,240], [1,0], 'f', Jacobian='jacob', Miter=2 )
PM, yp, Format='(3f10.6)', Title=' y(0) y(120) y(240)'
END
Example 2: Runge-Kutta Method
This example solves:
over the interval [0, 1] with the initial condition y(0) = 1 using the Runge-Kutta-Verner fifth-order and sixth-order method. The solution is y(t) = e–t.
.RUN
; Define function f.
FUNCTION f, t, y
RETURN, -y
END
; Call ODE with the keyword R_K_V set.
yp = ODE([0, 1], [1], 'f', /R_K_V)
; Output results.
PM, yp, Title = 'Solution'
; PV-WAVE prints: Solution 1.00000 0.367879
PM, yp(1) - EXP(-1), Title = 'Error'
; PV-WAVE prints: Error 0.00000
Example 3: Predator-Prey Problem
Consider a predator-prey problem with rabbits and foxes. Let r be the density of rabbits, and let f be the density of foxes. In the absence of any predator-prey interaction, the rabbits would increase at a rate proportional to their number, and the foxes would die of starvation at a rate proportional to their number. Mathematically, the model without species interaction is approximated by the following equations:
With species interaction, the rate at which the rabbits are consumed by the foxes is assumed to equal the value 2rf. The rate at which the foxes increase because they are consuming the rabbits, is equal to rf. Thus, the model differential equations to be solved are as follows:
For illustration, the initial conditions are taken to be
r(0) = 1 and
f (0) = 3. The interval of integration is 0
≤ t ≤ 40. In the program,
a(0) =
r and
a(1) =
f. Function ODE is then called with 100 time values from 0 to 40. The results are shown in
Figure 6-1: Predator-Prey Plot on page 253.
.RUN
; Define the function f.
FUNCTION f, t, a
yp = a
yp(0) = 2 * a(0) * (1 - a(1))
yp(1) = -a(1) * (1 - a(0))
RETURN, yp
END
; Set the initial values and time values.
a = [1, 3]
t = 40 * FINDGEN(100)/99
; Call ODE with R_K_V set to use the Runge-Kutta method.
a = ODE(t, a, 'f', /R_K_V)
; Use hardware font.
!P.Font = 0
; Plot the result.
PLOT, a(0, *), a(1, *), Psym = 2, XTitle = 'Density of Rabbits', $
YTitle = 'Density of Foxes'
Example 4: Stiff Problems and Changing Defaults
This problem is a stiff example (F5) from the test set of Enright and Pryce (1987). An initial step size of h = 10–7 is suggested by these authors. When solving a problem that is known to be stiff, using double precision is advisable. Function ODE is forced to use the suggested initial step size and double precision by using keywords.
y'0 = k0 ( –k1y0y1 + k2y3 – k3 y0y2 )
y'1 = – k0k1y0y1 + k4y3
y'2 = k0 ( –k3y0y2 + k5y3 )
y'3 = k0 ( k1y0y1 – k2y3 + k3 y0y2 )
y0(0) = 3.365 × 10–7
y1(0) = 8.261 × 10–3
y2(0) = 1.641 × 10–3
y3(0) = 9.380 × 10–6
k0 = 1011
k1 = 3.
k2 = 0.0012
k3 = 9.
k4 = 2 × 107
k5 = 0.001
.RUN
; Define the function.
FUNCTION f, t, y
k = [1d11, 3., .0012, 9., 2d7, .001]
yp = [k(0)*(-k(1)*y(0)*y(1)+k(2)*y(3)- $
k(3)*y(0)*y(2)),-k(0)*k(1)*y(0)*y(1)+ $
k(4)*y(3),k(0)*(-k(3)*y(0)*y(2) + $
k(5)*y(3)),k(0)* (k(1)*y(0)*y(1)- $
k(2)*y(3)+k(3)*y(0)*y(2))]
RETURN, yp
END
; Set up the values of the independent variable.
t = FINDGEN(500)/5e6
; Set the initial values.
y = [3.365e-7, 8.261e-3, 1.641e-3, 9.380e-6]
; Call ODE.
y = ODE(t, y, 'f', Hinit = 1d-7, /Double)
!P.Multi = [0, 2, 2]
!P.Font = 0
; Plot each variable on a separate axis.
PLOT, t, y(0, *), Title = '!8y!I0!5', XTicks=2
PLOT, t, y(1, *), Title = '!8y!I1!5', XTicks=2
PLOT, t, y(2, *), Title = '!8y!I2!5', XTicks=2
PLOT, t, y(3, *), Title = '!8y!I3!5', XTicks=2
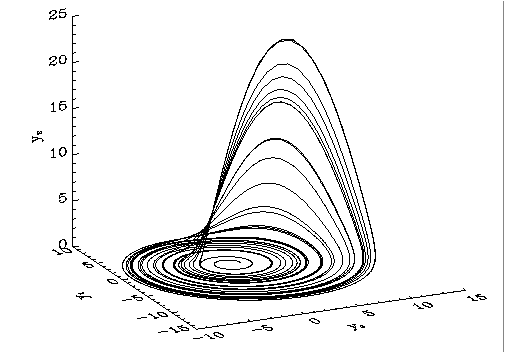
Example 5: Strange Attractors—The Rossler System
In this example, a strange attractor is illustrated. The strange attractor used is the Rossler system, a simple model of a truncated Navier-Stokes equation. The Rossler system is given by relation below.
y'0 = – y1 – y2
y'1 = y0 + a y1
y'2 = b + y0 y2 – c y2
The initial conditions and constants are shown below.
y0(0) = 1
y1(0) = 0
y2(0) = 0
a = 0.2
b = 0.2
c = 5.7
.RUN
; Define function f.
FUNCTION f, t, y
COMMON constants, a, b, c
; Define some common variables.
yp = y
yp(0) = -y(1) - y(2)
yp(1) = y(0) + a * y(1)
yp(2) = b + y(0) * y(2) - c * y(2)
RETURN, yp
END
COMMON constants, a, b, c
; Assign values to the common variables.
a = .2
b = .2
c = 5.7
; Set the number of values of the independent variable.
ntime = 5000
; Set the range of the independent variable to 0, ..., 200.
time_range = 200
; Allow up to 20,000 steps per value of the independent variable.
max_steps = 20000
t = FINDGEN(ntime)/(ntime - 1) * time_range
; Set the initial conditions.
y = [1, 0, 0]
; Call ODE using keywords Max_Steps and Double.
y = ODE(t, y, 'f', Max_Steps = max_steps, /Double)
!P.Charsize = 1.5
SURFACE, FINDGEN(2, 2), /Nodata, $
XRange = [MIN(y(0, *)), MAX(y(0, *))], $
YRange = [MIN(y(1, *)), MAX(y(1, *))], $
ZRange = [MIN(y(2, *)), MAX(y(2, *))], $
XTitle = '!6y!i0', YTitle = 'y!i1', $
ZTitle = 'y!i2', Az = 25, /Save
; Set up axes to plot solution. SURFACE draws the axes and defines
; the transformation used in PLOTS. The transformation is saved
; using keyword Save in SURFACE, then applied in PLOTS using T3d.
PLOTS, y(0, *), y(1, *), y(2, *), /T3d
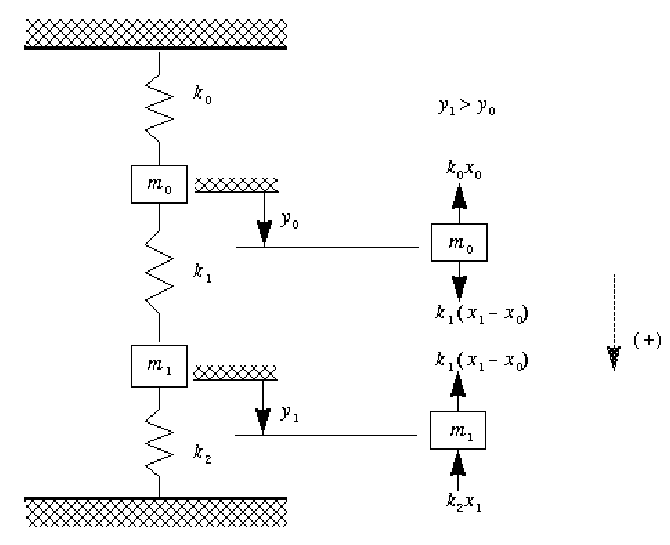
Example 6: Coupled, Second-order System
Consider the two-degrees-of-freedom system represented by the model (and corresponding free-body diagrams) in
Figure 6-4: Two-Degrees of Freedome System on page 258. Assuming
y1 is greater than
y0 causes the spring
k1 to be in tension, as seen by the tensile force
k1 (
y1 –
y0).
note | If y0 is taken to be greater than y1, then spring k1 is in compression, with the spring force k1 (y0 – y1). Both methods give correct results when a summation of forces is written. |
The differential equations of motion for the system are written as follows:
Thus:
If given the mass and spring constant values:
the following is true:
Now, in order to convert this problem into one which ODE can be used to solve, choose the following variables:
which yields the following equations:
The last four equations are the object of the return values of the user-supplied function in the exact order as previously specified.
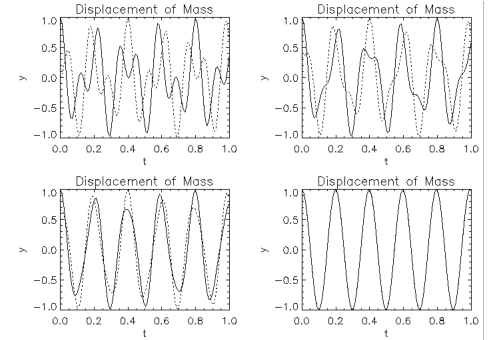
The example below loops through four different sets of initial values for
z. The results are shown in
Figure 6-5: Second Order Systems with Differential Initial Values on page 261.
.RUN
; Define a function.
FUNCTION f, t, z
k = [-2000, 1000]
RETURN, [z(2), z(3), k(0) * z(0) + k(1) * $
z(1), k(1) * z(0) + k(0) * z(1)]
END
; Independent variable, t, is between 0 and 1.
t = FINDGEN(1000)/999
; Place all four plots in one window.
!P.Multi = [0, 2, 2]
FOR i=0L, 3 DO BEGIN
z = [1, i/3., 0, 0]
z = ODE(t, z, 'f', Max_Steps = 1000, Hinit = 0.001, /R_K_V)
; Plot the displacement of m0 as a solid line.
PLOT, t, z(0, *), Thick = 2, Title = 'Displacement of Mass'
; Overplot the displacement of m1 as a dotted line.
OPLOT, t, z(1, *), Linestyle = 1, Thick = 2
The displacement for m0 is the solid line, and the dotted line represents the displacement for m1. Note that when the initial conditions for:
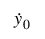 and
and 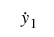
are equal, the displacement of the masses is equal for all values of the independent variable (as seen in the fourth plot). Also, the two principal modes of this problem occur when the following is true:
Fatal Errors
MATH_ODE_TOO_MANY_EVALS—Completion of the next step would make the number of function evaluations #, but only # evaluations are allowed.
MATH_ODE_TOO_MANY_STEPS—Maximum number of steps allowed; # used. The problem may be stiff.
MATH_ODE_FAIL—Unable to satisfy the error requirement. Tolerance = # may be too small.
Version 2017.0
Copyright © 2017, Rogue Wave Software, Inc. All Rights Reserved.
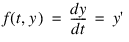
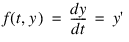
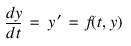
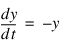
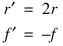
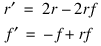
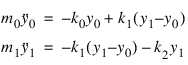
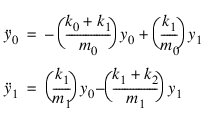
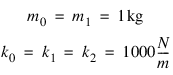
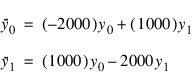
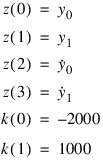
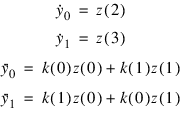
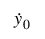 and
and