STRIP_SPLIT_PLOT Function (PV-WAVE Advantage)

IMSL Statistics Reference Guide > Analysis of Variance and Designed Experiments > STRIP_SPLIT_PLOT Function (PV-WAVE Advantage)

Analyzes data from strip-split-plot experiments. STRIP_SPLIT_PLOT also analyzes strip-split-plot experiments replicated at several locations.

Usage

result = STRIP_SPLIT_PLOT (n, n_locations, n_strip_a, n_strip_b, n_split, block, strip_a, strip_b, split, y)

Input Parameters

n—Number of missing and non-missing experimental observations. STRIP_PLOT verifies that:

where N_blocksi is equal to the number of blocks or replicates at the ith location.

n_locations—Number of locations. n_locations must be one or greater. If n_locations > 1 then the Locations keywords must be included as input to STRIP_SPLIT_PLOT.

n_strip_a—Number of levels associated with the strip-plot A factor. n_strip_a must be greater than one.

n_strip_b—Number of levels associated with the strip-plots B factor. n_strip_b must be greater than one.

n_split—Number of levels associated with the split factor. n_split must be greater than one.

block—Array of length n containing the block identifiers for each observation in y. Locations can have different numbers of blocks. Each block at a single location must be assigned a different identifier, but different locations can have the same assignments.

strip_a—Array of length n containing the strip-plot A level identifiers for each observation in y. Each level of this factor must be assigned a different integer. STRIP_SPLIT_PLOT verifies that the number of unique strip-plot identifiers is equal to n_strip_a.

strip_b—Array of length n containing the strip-plot B identifiers for each observation in y. Each level of this factor must be assigned a different integer. STRIP_SPLIT_PLOT verifies that the number of unique strip-plot identifiers is equal to n_strip_b.

split—Array of length n containing the split-plot level identifiers for each observation in y. Each level of this factor must be assigned a different integer. STRIP_SPLIT_PLOT verifies that the number of unique split-plot identifiers is equal to n_split.

y—Array of length n containing the experimental observations and any missing values. Missing values cannot be omitted. They are indicated by placing a NaN (Not a Number) at the appropriate positions in y. NaN can be defined by calling the MACHINE function. For example:

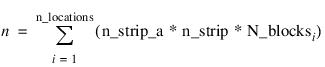
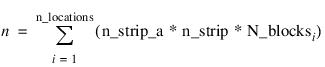
x = MACHINE(/Float)

y(i) = x.NaN

The location, strip-plot A, strip-plot B and split-plot for each observation in y are identified by the corresponding values in the Locations keyword, and the input parameters strip_a, strip_b, and split.

Returned Value

result—A two dimensional, 22 by 6 array containing the ANOVA table. Each row in this array contains values for one of the effects in the ANOVA table. The first value in each row, anova_tablei,0 = anova_table(i,0), identifies the source for the effect associated with values in that row. The remaining values in a row contain the ANOVA table values using the convention found in ANOVA Table Values.

Table 5-60: ANOVA Table Values
J	anova_tablei,j = anova_table(i,j)
0	Source Identifier (values described below)
1	Degrees of freedom
2	Sum of squares
3	Mean squares
4	F-statistic
5	p-value for this F-statistic

The Source Identifiers in the first column of anova_tablei,j are the only negative values in anova_table. Assignments of identifiers to ANOVA sources use the coding shown in ANOVA Assignment Identifiers.

Table 5-61: ANOVA Assignment Identifiers
Source Identifier	ANOVA Source
-1	LOCATIONS*
-2	BLOCK WITHIN LOCATION
-3	STRIP-PLOT A
-4	LOCATION × STRIP-PLOT A*
-5	STRIP-PLOT A ERROR
-6	SPLIT-PLOT
-7	SPLIT-PLOT × STRIP-PLOT A
-8	LOCATION × SPLIT-PLOT*
-9	SPLIT-PLOT ERROR
-10	LOCATION × SPLIT-PLOT × STRIP-PLOT A*
-11	STRIP-PLOT B
-12	LOCATION × STRIP-PLOT B*
-13	STRIP_PLOT B ERROR
-14	STRIP-PLOT A × STRIP-PLOT B
-15	LOCATION × STRIP-PLOT A × STRIP-PLOT B
-16	STRIP-PLOT A × STRIP-PLOT B ERROR
-17	SPLIT-PLOT × STRIP-PLOT B
-18	STRIP-PLOT A × STRIP-PLOT B × SPLIT-PLOT
-19	LOCATION × SPLIT-PLOT × STRIP-PLOT B*
-20	LOCATION × STRIP-PLOT A × STRIP-PLOT B × SPLIT-PLOT*
-21	STRIP-PLOT A × STRIP-PLOT B × SPLIT-PLOT ERROR
-22	CORRECTED TOTAL
* If n_locations = 1 sources involving location are set to missing (NaN).

Input Keywords

Double—If present and nonzero, double precision is used.

Locations—Array of length n containing the location identifiers for each observation in y. Unique integers must be assigned to each location in the study. This keyword is required when n_locations > 1.

Output Keywords

N_missing—Number of missing values, if any, found in y. Missing values are denoted with a NaN (Not a Number) value.

Cv—Array of length 3 containing the strip-plots and split-plot coefficients of variation. Cv(0) contains the strip-plot A C.V., Cv(1) contains the strip-plot B C.V., and Cv(2) contains the split-plot C.V.

Grand_mean—Mean of all the data across every location.

Strip_plot_a_means—Array of length n_strip_a containing the factor A strip-plot means.

Strip_plot_b_means—Array of length n_strip_b containing the strip-plot B means.

Split_plot_means—Array of length n_split containing the strip-plot B means.

Strip_plot_a_split_plot_means—A 2-dimensional array of size n_strip_a by n_split containing the means for all combinations of the factor A strip-plot and split-plots.

Split_plot_b_split_plot_means—A 2-dimensional array of size n_strip_b by n_split containing the means for all combinations of strip-plot B and split-plots.

Strip_plot_ab_means—A 2-dimensional array of size n_strip_a by n_strip_b containing the means for all combinations of strip-plots.

Treatment_means—Array of size (n_strip_a by n_strip_b by n_split) containing the treatment means. For i > 0 and j > 0, Treatment_meansi,j contains the mean of the observations, averaged over all locations, blocks and replicates, for the ith level of the strip-plot and the jth level of the split-plot.

Std_errors—Array of length 20 containing ten standard errors and their associated degrees of freedom. The standard errors are in the first 10 elements and their associated degrees of freedom are reported in Std_errors(10) through Std_errors(19). Refer to Standard Errors for a list of the standard errors and their associated degrees of freedom.

Table 5-62: Standard Errors
Element	Standard Error for Comparisons Between Two	Degrees of Freedom
Std_errors(0)	Strip-Plot A Means	Std_errors(10)
Std_errors(1)	Strip-Plot B Means	Std_errors(11)
Std_errors(2)	Split-Plot Means	Std_errors(12)
Std_errors(3)	Strip-Plot A Means at the same level of split-plots	Std_errors(13)
Std_errors(4)	Strip-Plot A Means at the same level of strip-plot B	Std_errors(14)
Std_errors(5)	Strip-Plot B Means at the same level of split-plots	Std_errors(15)
Std_errors(6)	Strip-Plot B Means at the same level of strip-plot A	Std_errors(16)
Std_errors(7)	Split-Plot Means at the same level of split-plot A	Std_errors(17)
Std_errors(8)	Split-Plot Means at the same level of strip-plot B	Std_errors(18)
Std_errors(9)	Treatment Means (same strip-plot A, strip-plot B and split-plot)	Std_errors(19)

N_blocks—Array of length n_locations containing the number of blocks, or replicates, at each location. This value must be greater than one.

Location_anova_table—A 3-dimensional array of size n_locations by 22 by 6 containing the ANOVA tables associated with each location. For each location, the 22 by 6 dimensional array corresponds to the ANOVA table for that location. For example, Location_anova_table(i,j,k) contains the value in the kth column and jth row of the returned anova-table for the ith location.

Anova_row_labels—Array containing the labels for each of the rows of the returned ANOVA table. The label for the ith row of the ANOVA table can be printed with PRINT, Anova_row_labels(i).

Discussion

STRIP_SPLIT_PLOT is capable of analyzing a wide variety of strip-split plot experiments, also referred to as strip-strip plot experiments. By default, STRIP_SPLIT_PLOT assumes that both strip-plot factors, and split-plots are fixed effects, and the location effects, if any, are random effects. The nature of randomization used in an experiment determines analysis of the data. Two popular forms of randomization in strip-plot and split-plot experiments are illustrated in Strip-Plot Experiment—Strip-Plots Completely Crossed and Split-Plot Experiment—Factor B Split-Plots Nested within Factor A Whole-Plots. In both experiments, the strip-plot factor, factor A, has 4 levels that are randomly assigned to a block or field in four strips.

Table 5-63: Strip-Plot Experiment—Strip-Plots Completely Crossed
		Factor A Strip-Plots
		A2	A1	A4	A3
Factor B Strip Plots	B3	A2B3	A1B3	A4B3	A3B3
	B1	A2B1	A1B1	A4B1	A3B1
	B2	A2B2	A1B2	A4B2	A3B2

In the strip-plot experiment, factor B, has 3 levels that are randomly assigned as strips across each of the four levels of factor A. In this case, factors A and B are completely crossed. The randomization applied to factor B is independent of the application of the strip-plots, factor A.

Contrast this to the randomization depicted in Split-Plot Experiment—Factor B Split-Plots Nested within Factor A Whole-Plots. In this split-plot experiment, the levels of factor B are nested within each level of factor A whole-plots. Factor B is randomized independently within each level of factor A. Unlike the strip-plot experiment, in the split-plot experiment different levels of factor B appear in the same row.

Table 5-64: Split-Plot Experiment—Factor B Split-Plots Nested within Factor A Whole-Plots
Whole-Plot Factor
A2	A1	A4	A3
A2B1	A1B3	A4B1	A3B3
A2B3	A1B1	A4B3	A3B1
A2B2	A1B2	A4B2	A3B2

A strip-split plot experiment is a strip-plot experiment with a third factor randomized within each level of strip-plot factor A, see Strip-Split Plot Experiment—Split-Plots nested within Strip-Plot Factors A. The third factor, referred to as the split-plot factor, is randomly assigned to experimental units within each level of strip-plot factor A. STRIP_SPLIT_PLOT analyzes strip-split plot experiments consisting of two strip-plot factors and one split-plot factor nested within strip-plot factors A and B.

Table 5-65: Strip-Split Plot Experiment—Split-Plots nested within Strip-Plot Factors A
		Factor A Strip Plots
		A2	A1	A4	A3
Factor B Strip Plots	B3	A2B3C2 A2B3C1	A1B3C1 A1B3C2	A4B3C2 A4B3C1	A3B3C2 A3B3C1
	B1	A2B1C1 A2B1C2	A1B1C1 A1B1C2	A4B1C2 A4B1C1	A3B1C2 A3B1C1
	B2	A2B2C2 A2B2C1	A1B2C1 A1B2C2	A4B2C1 A4B2C2	A3B2C2 A3B2C1

Strip-split plot experiments are closely related to split-split plot experiments, see Sub-Plot Factor C Nested Within Split-Plot Factor B, Nested Within Whole-Plot Factor A. The main difference between the two is that in strip-split plot experiments, the order of the levels for factor B are not applied randomly across factor A. Each level of factor B is constant across any row. In this example, the entire first row is assigned to the third level of factor B. In the equivalent split-split plot experiment, the levels of factor B are not constant across any row. The levels are randomized within each level of factor A.

Table 5-66: Sub-Plot Factor C Nested Within Split-Plot Factor B, Nested Within Whole-Plot Factor A
Whole Plot Factor A
A2	A1	A4	A3
A2B3C2 A2B3C1	A1B2C1 A1B2C2	A4B1C2 A4B1C1	A3B3C2 A3B3C1
A2B1C1 A2B1C2	A1B1C1 A1B1C2	A4B3C2 A4B3C1	A3B2C2 A3B2C1
A2B2C2 A2B2C1	A1B3C1 A1B3C2	A4B2C1 A4B2C2	A3B1C2 A3B1C1

In some studies, a strip-split-plot experiment is replicated at several locations. STRIP_SPLIT_PLOT can analyze strip-split plot experiments replicated at multiple locations, even when the number of blocks or replicates at each location might be different different. If only a single replicate or block is used at each location, then location should be treated as a blocking factor, with n_locations = 1. If n_locations = 1, it is assumed that either the experiment was conducted at multiple locations, each with a single block, or at a single location with more than one block or replicate at that location. When n_locations = 1, all entries associated with location in the ANOVA table will contain missing values.

However, if n_locations > 1, it is assumed the experiment was repeated at multiple locations, with blocking occurring at each location. Although the number of blocks at each location can be different, the number of levels for the strip-plot and split-plot factors strip-plots must be the same at each location. The locations associated with each of the observations in y are specified by the Locations keyword, which is a required keyword when n_locations > 1.

By default, locations are assumed to be random effects. Tests involving strip-plots use the interaction between strip-plots and locations as the error term for testing whether there are statistically significant differences among strip-plots. However, this assumes that the interaction of strip-plots and locations is not statistically significant. A test of this assumption is included in the ANOVA table. If any interactions between locations and strip-plot or split-plot factors are statistically significant, then the nature of these interactions should be explored since this impacts the interpretation of the significance of the treatment factors.

Similarly, when locations are assumed to be random effects, tests involving split-plots do not use the split-plot errors pooled across locations. Instead, the error term for split-plots is the interaction between locations and split-plots.

Suppose, for example, that a researcher wanted to conduct an agricultural experiment comparing the effectiveness of 4 fertilizers with 3 seed lots and 3 rates of application. One replicate of the experiment is conducted at each of the 3 farms. That is, only a single field at each location is assigned to this experiment.

Each field is divided into 4 vertical strips and 3 horizontal strips. The vertical strips are randomly assigned to fertilizers and the rows are randomly assigned to application rates. Fertilizers and application rates represent strip-plot factors A and B respectively. Seed lots are randomly assigned to three sub-divisions within each combination of strip-plots.

Table 5-67: Strip-Split Plot Experiment—Fertilizer, Application Rate, and Seed Lot Split-Plots
		Fertilizer Strip Plots
		F2	F1	F4	F3
Application Rate Strip Plot	R3	F2R3S1 F2R3S2 F2R3S3	F1R3S3 F1R3S2 F1R3S1	F4R3S3 F4R3S2 F4R3S1	F3R3S2 F3R3S1 F3R3S3
	R2	F2R1S3 F2R1S1 F2R1S2	F1R1S2 F1R1S3 F1R1S1	F4R1S3 F4R1S1 F4R1S2	F3R1S1 F3R1S2 F3R1S3
	R1	F2R2S1 F2R2S2 F2R2S3	F1R2S1 F1R2S3 F1R2S2	F4R2S2 F4R2S3 F4R2S1	F3R2S3 F3R2S1 F3R2S2

In this case, each farm is a blocking factor, fertilizers are factor A strip-plots, fertilizer application rates are factor B strip-plots, and seed lots are split-plots. The input array for the Locations keyword would contain integers from 1 to the number of farms.

Example

The experiment was conducted using a 2x2 strip_split plot arrangement with each of the four plots divided into 2 sub-divisions that were randomly assigned one of two split-plot levels. This was replicated 3 times producing an experiment with n = 2x2x2x3 = 24 observations.

; Total number of observations

n = 24

; Number of locations

n_locations = 1

; Number of factor A strip-plots within a location

n_strip_a = 2

; Number of factor B strip-plots within a location

n_strip_b = 2

; Number of split-plots within each Factor A strip-plot

n_split = 2

block =   [1, 1, 1, 1, 1, 1, 1, 1, $

           2, 2, 2, 2, 2, 2, 2, 2, $

           3, 3, 3, 3, 3, 3, 3, 3]

strip_a = [1, 1, 1, 1, 2, 2, 2, 2, $

           1, 1, 1, 1, 2, 2, 2, 2, $

           1, 1, 1, 1, 2, 2, 2, 2]

strip_b = [1, 1, 2, 2, 1, 1, 2, 2, $

           1, 1, 2, 2, 1, 1, 2, 2, $

           1, 1, 2, 2, 1, 1, 2, 2]

split =   [1, 2, 1, 2, 1, 2, 1, 2, $

           1, 2, 1, 2, 1, 2, 1, 2, $

           1, 2, 1, 2, 1, 2, 1, 2]

y = [30.0, 40.0, 38.9, 38.2, $

     41.8, 52.2, 54.8, 58.2, $

     20.5, 26.9, 21.4, 25.1, $

     26.4, 36.7, 28.9, 35.9, $

     21.0, 25.4, 24.0, 23.3, $

     34.4, 41.0, 33.0, 34.9]

aov = STRIP_SPLIT_PLOT(n, n_locations, n_strip_a, $

                       n_strip_b, n_split, block, $

                       strip_a, strip_b, split, y, $

                       Cv=cv, Grand_mean=grand_mean, $

                       Treatment_means=treatment_means, $

                       Strip_plot_a_means= $

                       strip_plot_a_means, $

                       Strip_plot_b_means=$

                       strip_plot_b_means, $

                       Split_plot_means=split_plot_means, $

                       Strip_plot_a_split_plot_means= $

                       strip_plot_a_split_plot_means, $

                       Strip_plot_b_split_plot_means= $

                       strip_plot_b_split_plot_means, $

                       Strip_plot_ab_means= $

                       strip_plot_ab_means, $

                       Std_errors=std_errors, $

                       N_blocks=n_blocks, $

                       Location_anova_table= $

                       location_anova_table)

labels = ['Location            ', $

          'Blocks              ', $

          'Strip-Plot A        ', $

          'Location x A        ', $

          'Strip-Plot A Error  ', $

          'Split-Plot          ', $

          'Split-Plot x A      ', $

          'Location x          ', $

          '  Split-Plot        ', $

          'Split-Plot Error    ', $

          'Location x          ', $

          '  Split-Plot x A    ', $

          'Strip-Plot B        ', $

          'Location x B        ', $

          'Strip-Plot B Error  ', $

          'A x B               ', $

          'Location x A x B    ', $

          'A x B Error         ', $

          'Split-Plot x B      ', $

          'Split-Plot x A x B  ', $

          'Location x          ', $

          '  Split-Plot x B    ', $

          'Location x          ', $

          '  Split-Plot x A x B', $

          'Split-Plot x A x    ', $

          '  B Error           ', $

          'Corrected Total     ']

; Print Analysis of Variance Table

PRINT, "             *** ANALYSIS OF VARIANCE TABLE ***"

PRINT, 'ID', 'DF', 'SSQ', 'MS', 'F-Test', 'p-Value', $

  Format='(A24, A5, A9, A8, A7, A8)'

idx = 0

FOR i=0L, (SIZE(aov))(1)-1 DO BEGIN & $

   PRINT, labels(idx), aov(i,0), aov(i,1), aov(i,2), $

     aov(i,3), aov(i,4), aov(i,5), Format= $

     '(A20, 1X, I3, 2X, F3.0, 2X, F7.2, 2X, F6.2, 2X, ' + $

     'F5.2, 2X, F6.3)' & $

   idx = idx + 1 & $

   IF idx LT N_ELEMENTS(labels)-1 THEN $

      WHILE STRPOS(labels(idx), ' ', 0) EQ 0 DO BEGIN & $

         PRINT, labels(idx) & idx = idx + 1 & $

      ENDWHILE & $

ENDFOR

PRINT, ''

PRINT, grand_mean, Format="('Grand mean: ', F9.6, '\012')"

PRINT, "Coefficient of Variation"

labels = ['Strip-Plot A:', 'Strip-Plot B:','Strip-Plot:  ']

FOR i=0L, 2 DO PRINT, labels(i), cv(i), Format='(A15, F12.4)'

PRINT, ''

PRINT, "****************************************************"

; Print the Treatment Means

PRINT, "Treatment Means"

idx = 0

FOR i=0L, n_strip_a-1, idx+1 DO $

   FOR j=0L, n_strip_b-1 DO $

      FOR k=0L, n_split-1 DO $

         PRINT, (i+1), (j+1), (k+1), $

         treatment_means(i,j,k), Format= "('" + $

         " Treatment[', I1, '][', I1, '][', I1, '] Mean:', F9.4)"

PRINT, ''

PRINT, std_errors(9), $

  Format='("Standard Error for Comparing Two ' + $

  'Treatment Means:", F9.6)'

PRINT, std_errors(19), Format="('(df=', F8.6, ')', '\012')"

; Perform multiple comparison using the LSD procedure

equal_means = MULTICOMP(REFORM(treatment_means, $

                (n_strip_a*n_strip_b*n_split)), $

                std_errors(19), std_errors(9)/SQRT(2.0), $

                /LSD, Alpha=0.05)

PM, equal_means, $

  Title="LSD Comparison: Size of Groups of Means"

PRINT, ''

PRINT, "****************************************************"

; Print the Strip-plot A Means.

PM, strip_plot_a_means, Title="Strip-plot A means"

PRINT, ''

PRINT, std_errors(0), $

  Format='("Standard Error for Comparing Two ' + $

  'Strip-Plot A Means:", F9.6)'

PRINT, std_errors(10), Format="('(df=', F8.6, ')', '\012')"

; Perform multiple comparison using the LSD procedure

equal_means = MULTICOMP(strip_plot_a_means, $

                std_errors(10), std_errors(0)/SQRT(2.0), $

                /LSD, Alpha=0.05)

PM, equal_means, $

  Title="LSD Comparison: Size of Groups of Means"

PRINT, ''

PRINT, "****************************************************"

; Print the Strip-plot B Means.

PM, strip_plot_b_means, Title="Strip-plot B means"

PRINT, ''

PRINT, std_errors(1), $

  Format='("Standard Error for Comparing Two ' + $

  'Strip-Plot B Means:", F9.6)'

PRINT, std_errors(11), Format="('(df=', F8.6, ')', '\012')"

; Perform multiple comparison using the LSD procedure

equal_means = MULTICOMP(strip_plot_b_means, $

                std_errors(11), std_errors(1)/SQRT(2.0), $

                /LSD, Alpha=0.05)

PM, equal_means, $

  Title="LSD Comparison: Size of Groups of Means"

PRINT, ''

PRINT, "****************************************************"

; Print the Split-plot Means.

PM, split_plot_means, Title="Split-plot Means"

PRINT, ''

PRINT, std_errors(2), $

  Format='("Standard Error for Comparing Two ' + $

  'Split-Plot Means:", F9.6)'

PRINT, std_errors(12), Format="('(df=', F8.6, ')', '\012')"

; Perform multiple comparison using the LSD procedure

equal_means = MULTICOMP(split_plot_means, $

                std_errors(12), std_errors(2)/SQRT(2.0), $

                /LSD, Alpha=0.05)

PM, equal_means, $

  Title="LSD Comparison: Size of Groups of Means"

PRINT, ''

PRINT, "****************************************************"

; Print the Strip-plot A by Split-plot Means.

PM, strip_plot_a_split_plot_means,  $

Title="Strip-plot A by Split-plot Means"

PRINT, ''

PRINT, std_errors(3), $

  Format='("Standard Error for Comparing Two Means:", F9.6)'

PRINT, std_errors(13), Format="('(df=', F8.6, ')', '\012')"

; Perform multiple comparison using the LSD procedure

equal_means = MULTICOMP( $

                REFORM(strip_plot_a_split_plot_means, $

                n_strip_a*n_split), $

                std_errors(13), std_errors(3)/SQRT(2.0), $

                /LSD, Alpha=0.05)

PM, equal_means, $

  Title="LSD Comparison: Size of Groups of Means"

PRINT, ''

PRINT, "****************************************************"

; Print the Strip-plot A by Split-plot B Means.

PM, strip_plot_ab_means, $

Title="Strip-plot A by Strip-plot B Means"

PRINT, ''

PRINT, std_errors(4), $

  Format='("Standard Error for Comparing Two Means:", F9.6)'

PRINT, std_errors(14), Format="('(df=', F8.6, ')', '\012')"

; Perform multiple comparison using the LSD procedure

equal_means = MULTICOMP(REFORM(strip_plot_ab_means, $

                n_strip_a*n_strip_b), $

                std_errors(14), std_errors(4)/SQRT(2.0), $

                /LSD, Alpha=0.05)

PM, equal_means, $

   Title="LSD Comparison: Size of Groups of Means"

PRINT, ''

PRINT, "****************************************************"

; Print the Strip-plot B by Split-plot Means.

PM, strip_plot_b_split_plot_means, $

   Title="Strip-plot B by Split-plot Means"

PRINT, ''

PRINT, std_errors(5), $

  Format='("Standard Error for Comparing Two Means:", F9.6)'

PRINT, std_errors(15), Format="('(df=', F8.6, ')', '\012')"

PRINT, ''

; Perform multiple comparison using the LSD procedure

equal_means = MULTICOMP($

                REFORM(strip_plot_b_split_plot_means, $

                n_strip_b*n_split), $

                std_errors(15), std_errors(5)/SQRT(2.0), $

                /LSD, Alpha=0.05)

PM, equal_means, $

  Title="LSD Comparison: Size of Groups of Means"

PRINT, ''

Output

*** ANALYSIS OF VARIANCE TABLE ***

                      ID   DF      SSQ      MS F-Test p-Value

Location              -1  NaN      NaN     NaN    NaN     NaN

Blocks                -2   2.  1310.28  655.14  14.53   0.061

Strip-Plot A          -3   1.   858.01  858.01  40.37   0.024

Location x A          -4  NaN      NaN     NaN    NaN     NaN

Strip-Plot A Error    -5   2.    42.51   21.26   1.48   0.385

Split-Plot            -6   1.   163.80  163.80  41.22   0.003

Split-Plot x A        -7   1.    11.34   11.34   2.85   0.166

Location x            -8  NaN      NaN     NaN    NaN     NaN

  Split-Plot

Split-Plot Error      -9   4.    15.90    3.97   1.56   0.338

Location x           -10  NaN      NaN     NaN    NaN     NaN

  Split-Plot x A

Strip-Plot B         -11   1.    17.17   17.17   0.47   0.565

Location x B         -12  NaN      NaN     NaN    NaN     NaN

Strip-Plot B Error   -13   2.    73.51   36.75   2.85   0.260

A x B                -14   1.     1.55    1.55   0.12   0.762

Location x A x B     -15  NaN      NaN     NaN    NaN     NaN

A x B Error          -16   2.    25.82   12.91   5.08   0.080

Split-Plot x B       -17   1.    46.76   46.76  18.39   0.013

Split-Plot x A x B   -18   1.     0.51    0.51   0.20   0.677

Location x           -19  NaN      NaN     NaN    NaN     NaN

  Split-Plot x B

Location x           -20  NaN      NaN     NaN    NaN     NaN

  Split-Plot x A x B

Split-Plot x A x     -21   4.    10.17    2.54    NaN     NaN

  B Error

Corrected Total      -22  23.  2577.33     NaN    NaN     NaN

Grand mean: 33.870834

Coefficient of Variation

  Strip-Plot A:     13.6116

  Strip-Plot B:     17.8986

  Strip-Plot:        5.8854

****************************************************

Treatment Means

  Treatment[1][1][1] Mean:  23.8333

  Treatment[1][1][2] Mean:  30.7667

  Treatment[1][2][1] Mean:  28.1000

  Treatment[1][2][2] Mean:  28.8667

  Treatment[2][1][1] Mean:  34.2000

  Treatment[2][1][2] Mean:  43.3000

  Treatment[2][2][1] Mean:  38.9000

  Treatment[2][2][2] Mean:  43.0000

Standard Error for Comparing Two Treatment Means: 1.302029

(df=4.000000)

LSD Comparison: Size of Groups of Means

****************************************************

Strip-plot A means

      27.8917

      39.8500

Standard Error for Comparing Two Strip-Plot A Means: 1.882171

(df=2.000000)

LSD Comparison: Size of Groups of Means

****************************************************

Strip-plot B means

      33.0250

      34.7167

Standard Error for Comparing Two Strip-Plot B Means: 2.474972

(df=2.000000)

LSD Comparison: Size of Groups of Means

****************************************************

Split-plot Means

      31.2583

      36.4833

Standard Error for Comparing Two Split-Plot Means: 0.813813

(df=4.000000)

LSD Comparison: Size of Groups of Means

****************************************************

Strip-plot A by Split-plot Means

      25.9667      29.8167

      36.5500      43.1500

Standard Error for Comparing Two Means: 1.150906

(df=4.000000)

LSD Comparison: Size of Groups of Means

****************************************************

Strip-plot A by Strip-plot B Means

      27.3000      28.4833

      38.7500      40.9500

Standard Error for Comparing Two Means: 2.074280

(df=2.000000)

LSD Comparison: Size of Groups of Means

****************************************************

Strip-plot B by Split-plot Means

      29.0167      37.0333

      33.5000      35.9333

Standard Error for Comparing Two Means: 0.920673

(df=4.000000)

LSD Comparison: Size of Groups of Means

Version 2017.0