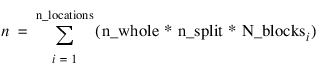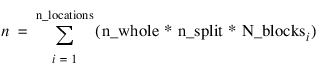SPLIT_PLOT Function (PV-WAVE Advantage)
Analyzes a wide variety of split-plot experiments with fixed, mixed or random factors. The whole-plots can be assigned to experimental units using either a completely randomized or randomized complete block design. SPLIT_PLOT also analyzes split-plot experiments replicated at several locations.
Usage
result = SPLIT_PLOT(n, n_locations, n_whole, n_split, rep, whole, split, y)
Input Parameters
n—Number of missing and non-missing experimental observations. SPLIT_PLOT verifies that:
where N_blocksi is equal to the number of blocks or replicates at the ith location.
n_locations—Number of locations. n_locations must be one or greater. If n_locations > 1, then the Locations keyword must be included as input to SPLIT_PLOT.
n_whole—Number of levels associated with the whole-plot factor. n_whole must be greater than one.
n_split—Number of levels associated with the split-plot factor. n_split must be greater than one.
rep—Array of length n containing the block, or replicate, identifiers for each observation in y. Locations can have different numbers of blocks or replicates. Each block or replicate at a single location must be assigned a different identifier, but different locations can have the same assignments.
whole—Array of length n containing the whole-plot identifiers for each observation in y. Each level of the whole-plot factor must be assigned a different integer. SPLIT_PLOT verifies that the number of unique whole-plot identifiers is equal to n_whole.
split—Array of length n containing the split-plot identifiers for each observation in y. Each level of the split-plot factor must be assigned a different integer. SPLIT_PLOT verifies that the number of unique split-plot identifiers is equal to n_split.
y—Array of length n containing the experimental observations and any missing values. Missing values cannot be omitted. They are indicated by placing a NaN (Not a Number) at the appropriate positions in y. NaN can be defined by calling the MACHINE function. For example:
x = MACHINE(/Float)
y(i) = x.NaN
At a single location, only one missing value per whole-plot is allowed. The location, whole-plot and split-plot for each observation in y are identified by the corresponding values in the input parameters whole and split, and the Locations keyword.
Returned Value
result—A two dimensional, 11 by 6 array containing the ANOVA table. Each row in this array contains values for one of the effects in the ANOVA table. The first value in each row,
anova_tablei,0 =
anova_table(
i,0), identifies the source for the effect associated with values in that row. The remaining values in a row contain the ANOVA table values using the convention found in
ANOVA Table Values.
The Source Identifiers in the first column of
anova_tablei,j are the only negative values in
anova_table. Assignments of identifiers to ANOVA sources use the coding shown in
ANOVA Source Identifiers.
Input Keywords
Double—If present and nonzero, double precision is used.
Locations—Array of length n containing the location identifiers for each observation in y. Unique integers must be assigned to each location in the study. This keyword is required when n_locations > 1.
Loc_fixed—A characteristic controlling whether the location factor is treated as a fixed or random effect, when n_locations > 1. If the Loc_fixed keyword is set and nonzero, then the location factor is treated as a fixed effect. Otherwise, by default, the location factor is treated as a random effect.
Crd—Whole-plot randomization characteristic. If the Crd keyword is set and nonzero, whole-plots are completely randomized to whole-plot experimental units. Otherwise, by default, whole-plots are assigned to whole-plot experimental units using a randomized complete block design (RCBD).
Whole_random—Whole-plot characteristic. If the Whole_random keyword is set and nonzero, then the whole-plot factor is a random effect. Otherwise, by default, the whole-plot factor is a fixed effect.
Split_random—Split-plot characteristic. If the Split_random keyword is set and nonzero, then the split-plot factor is a random effect. Otherwise, by default, the split-plot factor is a fixed effect.
Output Keywords
N_missing—Number of missing values, if any, found in y. Missing values are denoted with a NaN (Not a Number) value.
Cv—Array of length 2 containing the whole-plot and split-plot coefficients of variation. Cv(0) contains the whole-plot C.V., and Cv(1) contains the split-plot C.V.
Grand_mean—Mean of all the data across every location.
Whole_plot_means—Array of length n_whole containing the whole-plot means.
Split_plot_means—Array of length n_split containing the split-plot means.
Treatment_means—Array of size (n_whole by n_split) containing the treatment means. For i > 0 and j > 0, Treatment_meansi,j contains the mean of the observations, averaged over all locations, blocks and replicates, for the jth split-plot within the ith whole-plot.
Std_errors—Array of length 10 containing 5 standard errors and their associated degrees of freedom. Refer to
Standard Errors for a list of the standard errors and their associated degrees of freedom.
N_blocks—Array of length n_locations containing the number of blocks, or replicates, at each location.
Block_ss—A 2-dimensional array of size n_locations by 2 containing the sum of squares for blocks and their associated degrees of freedom for each location.
Whole_plot_ss—A 2-dimensional array of size n_locations by 2 containing the sum of squares for whole-plots and their associated degrees of freedom for each location.
Split_plot_ss—A 2-dimensional array of size n_locations by 2 containing the sum of squares for split-plots and their associated degrees of freedom for each location.
Wholexsplit_plot_ss—A 2-dimensional array of size n_locations by 2 containing the sum of squares for whole-plot by split-plot interaction and their associated degrees of freedom for each location.
Whole_plot_error_ss—A 2-dimensional array of size n_locations by 2 containing the error sum of squares for whole-plot and their associated degrees of freedom for each location.
Split_plot_error_ss—A 2-dimensional array of size n_locations by 2 containing the error sum of squares for split-plot and their associated degrees of freedom for each location.
Total_ss—A 2-dimensional array of size n_locations by 2 containing the corrected total sum of squares and their associated degrees of freedom for each location.
Anova_row_labels—Array containing the labels for each of the rows of the returned ANOVA table. The label for the ith row of the ANOVA table can be printed with PRINT, Anova_row_labels(i).
Discussion
SPLIT_PLOT is capable of analyzing a wide variety of split-plot experiments. Whole-plot and split-plot factors can each be designated as either fixed or random, allowing for experiments with fixed, random or mixed treatment effects. By default, SPLIT_PLOT assumes that the whole-plot and split-plot treatment factors are fixed effects and the location factor is a random effect. Whole-plot or split-plot factors can each be declared as random effects by setting the keywords Whole_random and Split_random, respectively.
Split-plot experimental designs can also vary in the assignment of the whole-plot factor to its experimental units. In some cases, this assignment is completely random. For example, in a drug study the experimental unit might be the subject receiving a treatment. The whole-plot factor, possibly different treatments, could be assigned in one of two ways. Each subject could receive only one treatment or each could receive all treatments over an appropriate period of time. If each subject received only a single randomly selected treatment, then this design constitutes a completely randomized design for the whole-plot factor, and the keyword Crd must be set.
On the other hand, if each subject receives every treatment in random order, then the subject is a blocking factor, and this sampling scheme constitutes a randomized complete block design (RCBD). In this case, it is necessary to assume that there are no carry-over effects from one treatment to another. This sampling scheme is the default setting.
A similar randomization choice occurs in agricultural field trials. A trial designed to test different fertilizers and different seed lots can be conducted in one of two ways. The whole-plot factor, fertilizer, can be applied to different fields, or each can be applied to sub-divisions of these fields. In either case, a field is the whole-plot experimental unit. In the first case in which only a single randomly selected fertilizer is applied to a single field, the whole-plot factor is not blocked and this scheme is called as a completely randomized design (CRD), and the keyword Crd must be set. However, if fertilizers are applied to sub-plots within a field, then the whole-plot factor is blocked within fields and this assignment is referred to as an RCBD. By default, this routine assumes that levels of the whole-plot factor are randomly assigned within blocks.
The essential distinction between split-plot experiments and completely randomized or randomized complete block experiments is the presence of a second factor that is blocked, or nested, within each level of the whole-plot factor. This second factor is referred to as the split-plot factor, see
Split-Plot Experiments—Split-Plot B Nested within Whole-Plot A. If levels of this factor were completely randomized, then two or more treatments with the same split-plot level could be assigned to the same whole-plot level, see
Completely Randomized Experiments—Both Factors Randomized.
In some studies, a split-plot experiment is replicated at several locations. SPLIT_PLOT can also analyze split-plot experiments replicated at multiple locations, even when the number of blocks or replicates at each location are different. If only a single replicate or block is used at each location, then location should be treated as a blocking factor, with n_locations set equal to one. If n_locations = 1, it is assumed that the experiment was conducted at a single location with more than one block or replicate at that location. In this case, the four entries associated with location in the ANOVA table will contain missing values.
However, if n_locations > 1, it is assumed the experiment was repeated at multiple locations, with replication or blocking occurring at each location. Although the number of blocks, or replicates, at each location can be different, the number of levels for whole-plot and split-plot factors, n_whole and n_split, must be the same at each location. The location associated with y(i) is specified in Location(i), which is a required input keyword when n_locations > 1.
By default, locations are assumed to be random effects. However, they can be specified as fixed effects by setting the optional keyword loc_fixed. This setting changes the calculations of the F-tests for whole-plot and split-plot factors. If locations are assumed to be fixed effects, then the whole-plot and split-plot errors at each location are pooled to form the whole-plot and split-plot errors. This can dramatically increase the degrees of freedom associated with the F-test for the treatment factors, resulting in smaller p-values. However, pooling the error terms from different locations requires experimenters to assume that the errors at each location are approximately the same. This should be verified using a test for homogeneity of variance, such as Bartlett’s or Levene’s test.
On the other hand, if locations are assumed to be random effects, then tests involving whole-plots use the interaction between whole-plots and locations as the error term for testing whether there are statistically significant differences among whole-plot factor levels. However, this assumes that the interaction of whole-plots and locations is not statistically significant. A test of this assumption uses the pooled whole-plot error. If the interaction between whole-plots and locations is statistically significant, then the nature of that interaction should be explored since it impacts the interpretation of the significance of the whole-plot treatment factor.
Similarly, when locations are assumed to be random effects, tests involving split-plots do not use the split-plot errors pooled across locations. Instead, the error term for split plots is the interaction between locations and split-plots. The split-plot by whole-plot interaction is tested against the location by split-plot by whole-plot interaction.
Suppose, for example, that a researcher wanted to conduct an agricultural experiment comparing the effectiveness of 4 fertilizers with 4 seed lots. One replicate of the experiment is conducted at each of the 3 farms. That is, only a single field at each location is assigned to this experiment.
The field at each farm is divided into 4 whole-plots and the fertilizers are randomly assigned to each of the 4 whole-plots. Each whole-plot is then further divided into 4 split-plots, and the seed lots are randomly assigned to these split-plots.
In this case, each farm is a blocking factor, fertilizers are whole-plots and seed lots are split-plots. The input parameter rep would contain integers from 1 to the number of farms.
However, if each farm allocated more than a single field for this study, then each farm would be treated as a different location with n_locations set equal to the number of farms, and fields would be treated as blocking factor. The input parameter rep would contain integers from 1 to the number fields used in a farm, and the Locations keyword would contain integers from 1 to the number of farms.
In summary this routine can analyze 3x2x2x2=24 different experimental situations, depending upon the settings of:

Locations (none, fixed or random): specified by setting
n_locations,
Locations and
Loc_fixed (random is the default).

Whole-plot sampling (CRD or RCBD): specified by setting the
Crd keyword (RCBD is the default).

Whole-plot effect (fixed or random): specified by setting
Whole_random (fixed effects is the default).

Split-plot effect (fixed or random): specified by setting
Split_random (fixed effects is the default).
The default condition depends upon the value for n_locations. If n_locations > 1, locations are assumed to be a random effect. Assignment of experimental units to whole-plots is assumed to use a RCBD design and both whole-plots and split-plots are assumed to be fixed effects.
Example
This example uses data from a split-plot design consisting of 2 whole-plots and 4 split-plots.
; Total number of observations
n = 24
; Number of locations
n_locations = 1
; Number of Whole-plots within a location
n_whole = 2
; Number of Split-plots within a location, Whole-plot
n_split = 4
rep = [1, 1, 1, 1, 1, 1, 1, 1, $
2, 2, 2, 2, 2, 2, 2, 2, $
3, 3, 3, 3, 3, 3, 3, 3]
whole = [1, 1, 1, 1, 2, 2, 2, 2, $
1, 1, 1, 1, 2, 2, 2, 2, $
1, 1, 1, 1, 2, 2, 2, 2]
split = [1, 2, 3, 4, 1, 2, 3, 4, $
1, 2, 3, 4, 1, 2, 3, 4, $
1, 2, 3, 4, 1, 2, 3, 4]
y = [30.0, 40.0, 38.9, 38.2, $
41.8, 52.2, 54.8, 58.2, $
20.5, 26.9, 21.4, 25.1, $
26.4, 36.7, 28.9, 35.9, $
21.0, 25.4, 24.0, 23.3, $
34.4, 41.0, 33.0, 34.9]
aov = SPLIT_PLOT(n, n_locations, n_whole, n_split, $
rep, whole, split, y, $
N_missing=n_missing, Cv=cv, $
Grand_mean=grand_mean, $
Whole_plot_means=whole_plot_means, $
Split_plot_means=split_plot_means, $
Treatment_means=treatment_means, $
Std_errors=std_errors, $
N_blocks=n_blocks, $
Block_ss=block_ss, $
Whole_plot_ss=whole_plot_ss, $
Split_plot_ss=split_plot_ss, $
Wholexsplit_plot_ss=wholexsplit_plot_ss, $
Whole_plot_error_ss=whole_plot_error_ss, $
Split_plot_error_ss=split_plot_error_ss, $
Total_ss=total_ss)
labels = ['Location ', $
'Block Within ', $
' Location' , $
'Whole-Plot ', $
'Location x ', $
' Whole-Plot' , $
'Whole-Plot Error', $
'Split-Plot ', $
'Location x ', $
' Split-Plot' , $
'Whole-Plot x ', $
' Split-Plot' , $
'Location x ', $
' Whole-Plot x' , $
' Split-Plot' , $
'Split-Plot Error', $
'Corrected Total ']
; Print header
PRINT, " *** ANALYSIS OF VARIANCE TABLE ***"
PRINT, 'ID', 'DF', 'SSQ', 'MS', 'F-test', 'p-Value', $
Format='(A21, A6, A10, A8, A8, A8)'
idx = 0
FOR i=0L, (SIZE(aov))(1)-1 DO BEGIN & $
PRINT, labels(idx), aov(i,0), aov(i,1), aov(i,2), $
aov(i,3), aov(i,4), aov(i,5), Format= $
'(A16, 2X, I3, 3X, F3.0, 2X, F8.2, 2X, F6.2, 2X, ' + $
'F5.2, 4X, F5.3)' & $
idx = idx + 1 & $
IF idx LT N_ELEMENTS(labels)-1 THEN $
WHILE STRPOS(labels(idx), ' ', 0) EQ 0 DO BEGIN & $
PRINT, labels(idx) & idx = idx + 1 & $
ENDWHILE & $
ENDFOR
PRINT, ''
PRINT, grand_mean, Format="('Grand mean: ', F9.6, '\012')"
PM, treatment_means, Title="Treatment means"
PRINT, ''
PM, whole_plot_means, Title="Whole-plot Means"
PRINT, ''
PM, split_plot_means, Title="Split-plot Means"
Output
*** ANALYSIS OF VARIANCE TABLE ***
ID DF SSQ MS F-test p-Value
Location -1 NaN NaN NaN NaN NaN
Block Within -2 2. 1310.28 655.14 30.82 0.031
Location
Whole-Plot -3 1. 858.01 858.01 40.37 0.024
Location x -4 NaN NaN NaN NaN NaN
Whole-Plot
Whole-Plot Error -5 2. 42.51 21.26 2.03 0.173
Split-Plot -6 3. 227.73 75.91 7.26 0.005
Location x -7 NaN NaN NaN NaN NaN
Split-Plot
Whole-Plot x -8 3. 13.40 4.47 0.43 0.737
Split-Plot
Location x -9 NaN NaN NaN NaN NaN
Whole-Plot x
Split-Plot
Split-Plot Error -10 12. 125.39 10.45 NaN NaN
Corrected Total -11 23. 2577.33 NaN NaN NaN
Grand mean: 33.870834
Treatment Means
23.8333 30.7667 28.1000 28.8667
34.2000 43.3000 38.9000 43.0000
Whole-plot Means
27.8917
39.8500
Split-plot Means
29.0167
37.0333
33.5000
35.9333
Version 2017.0
Copyright © 2017, Rogue Wave Software, Inc. All Rights Reserved.