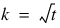 blocks.
blocks. 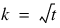 .
.J | anova_tablei,j = anova_table(i,j) |
0 | Source Identifier (values described below) |
1 | Degrees of freedom |
2 | Sum of squares |
3 | Mean squares |
4 | F-statistic |
5 | p-value for this F-statistic |
Source Identifier | ANOVA Source |
–1 | LOCATIONS* |
–2 | REPLICATES |
–3 | TREATMENTS(unadjusted) |
–4 | TREATMENTS(adjusted) |
–5 | BLOCKS(adjusted) |
–6 | INTRA-BLOCK ERROR |
–7 | CORRECTED TOTAL |
* If N_locations = 1 rows involving location are set to missing (NaN). | |
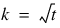 .
.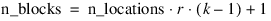
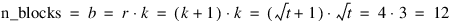
Replicate I | Replicate II |
Block 1 (T1, T2, T3) | Block 4 (T1, T4, T7) |
Block 2 (T4, T5, T6) | Block 5 (T2, T5, T8) |
Block 3 (T7, T8, T9) | Block 6 (T3, T6, T9) |
Replicate III | Replicate IV |
Block 7 (T1, T5, T9) | Block 10 (T1, T6, T8) |
Block 8 (T2, T6, T7) | Block 11 (T2, T4, T9) |
Block 9 (T3, T4, T8) | Block 12 (T3, T5, T7) |
SOURCE | DF | Sum of Squares | Mean Squares |
REPLICATES | r – 1 | SSR | MSR |
TREATMENTS(unadj) | t – 1 | SST | MST |
TREATMENTS(adj) | t – 1 | SSTa | MSTa |
BLOCKS(adj) | 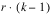 | SSBa | MSBa |
INTRA-BLOCK ERROR | 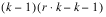 | SSI | MSI |
TOTAL | 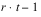 | SSTot | |
SOURCE | DF | Sum of Squares | Mean Squares |
LOCATIONS | p – 1 | SSL | MSL |
REPLICATES WITHIN LOCATIONS | p(r – 1) | SSR | MSR |
TREATMENTS(unadj) | t – 1 | SST | MST |
TREATMENTS(adj) | t – 1 | SSTa | MSTa |
BLOCKS(adj) | 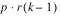 | SSB | MSB |
INTRA-BLOCK ERROR | 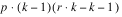 | SSI | MSI |
TOTAL | 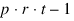 | SSTot | |
; Total number of observations
n = 80
; Number of locations
n_locations = 1
; Number of treatments
n_treatments = 16
; Number of replicates
n_reps = 5
; Total number of blocks
n_blocks = 20
rep = [ $
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, $
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, $
3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, $
4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, $
5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5 ]
block = [ $
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, $
4, 4, 4, 4, 5, 5, 5, 5, 6, 6, 6, 6, $
7, 7, 7, 7, 8, 8, 8, 8, 9, 9, 9, 9, $
10, 10, 10, 10, 11, 11, 11, 11, 12, 12, 12, 12, $
13, 13, 13, 13, 14, 14, 14, 14, 15, 15, 15, 15, $
16, 16, 16, 16, 17, 17, 17, 17, 18, 18, 18, 18, $
19, 19, 19, 19, 20, 20, 20, 20 ]
treatments = [ $
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, $
14, 15, 16, 1, 5, 9, 13, 10, 2, 14, 6, 7, 15, $
3, 11, 16, 8, 12, 4, 1, 6, 11, 16, 5, 2, 15, $
12, 9, 14, 3, 8, 13, 10, 7, 4, 1, 14, 7, 12, $
13, 2, 11, 8, 5, 10, 3, 16, 9, 6, 15, 4, 1, $
10, 15, 8, 9, 2, 7, 16, 13, 6, 3, 12, 5, 14, $
11, 4 ]
y = [ $
147, 152, 167, 150, 127, 155, 162, 172, $
147, 100, 192, 177, 155, 195, 192, 205, $
140, 165, 182, 152, 97, 155, 192, 142, $
155, 182, 192, 192, 182, 207, 232, 162, $
155, 132, 177, 152, 182, 130, 177, 165, $
137, 185, 152, 152, 185, 122, 182, 192, $
220, 202, 175, 205, 205, 152, 180, 187, $
165, 150, 200, 160, 155, 177, 185, 172, $
147, 112, 177, 147, 180, 205, 190, 167, $
172, 212, 197, 192, 177, 220, 205, 225 ]
aov = LATTICE_DESIGN(n, n_locations, n_reps, n_blocks, $
n_treatments, rep, block, treatments, $
y, Grand_mean=grand_mean, Cv=cv, $
Treatment_means=treatment_means, $
Std_err=std_err)
labels = ['Locations ', $
'Replicates ', $
'Treatments ', $
' (unadjusted)' , $
'Treatments ', $
' (adjusted)' , $
'Blocks (adjusted)', $
'Intra-Block Error', $
'Corrected Total ']
; Print Analysis of Variance Table
PRINT, " *** ANALYSIS OF VARIANCE TABLE ***"
PRINT, 'ID', 'DF', 'SSQ', 'MS', 'F-test', 'P-Value', $
Format='(A21, A7, A8, A9, A8, A8)' & $
idx = 0
FOR i=0L, (SIZE(aov))(1)-1 DO BEGIN & $
PRINT, labels(idx), aov(i,0), aov(i,1), $
aov(i,2), aov(i,3), aov(i,4), aov(i,5), Format= $
'(A17, 1X, I3, 2X, F3.0, 2X, F8.2, 2X, F7.2, 2X, ' + $
'F5.2, 2X, F7.3)' & $
idx = idx + 1 & $
IF idx LT N_ELEMENTS(labels)-1 THEN $
WHILE STRPOS(labels(idx), ' ', 0) EQ 0 DO BEGIN & $
PRINT, labels(idx) & idx = idx + 1 & $
ENDWHILE & $
ENDFOR
PRINT, ''
PRINT, grand_mean, $
Format='("Adjusted Grand Mean :", F8.3)'PRINT, cv, Format='("Coefficient of Variation:", F8.3)'PRINT, ''
PRINT, "Adjusted Treatment Means:"
FOR i=0L, n_treatments-1 DO $
PRINT, (i+1), treatment_means(i), Format= $
"(2X, 'Treatment[', I2, '] Mean:', F10.4)"
PRINT, ''
PRINT, std_err(0), $
Format='("Standard Error for Comparing Two Treatment ' + $'Means: ", F9.6, I1)'
PRINT, FIX(std_err(3)), Format='("(df=", I2, ")")'PRINT, ''
; Perform multiple comparison using the LSD procedure
equal_means = MULTICOMP(treatment_means, $
std_err(3), std_err(2)/SQRT(2.0), $
/LSD, Alpha=0.05)
PM, equal_means, $
Title="LSD Comparison: Size of Groups of Means"
*** ANALYSIS OF VARIANCE TABLE ***
ID DF SSQ MS F-test P-Value
Locations -1 NaN NaN NaN NaN NaN
Replicates -2 4. 6524.50 1631.12 NaN NaN
Treatments -3 15. 27297.00 1819.80 4.12 0.000
(unadjusted)
Treatments -4 15. 21271.20 1418.08 4.21 0.000
(adjusted)
Blocks (adjusted) -5 15. 11339.28 755.95 NaN NaN
Intra-Block Error -6 45. 15173.23 337.18 NaN NaN
Corrected Total -7 79. 60334.00 NaN NaN NaN
Adjusted Grand Mean : 171.450
Coefficient of Variation: 10.710
Adjusted Treatment Means:
Treatment[ 1] Mean: 166.4533
Treatment[ 2] Mean: 160.7527
Treatment[ 3] Mean: 183.6289
Treatment[ 4] Mean: 175.6298
Treatment[ 5] Mean: 162.6807
Treatment[ 6] Mean: 167.6716
Treatment[ 7] Mean: 168.3822
Treatment[ 8] Mean: 176.5731
Treatment[ 9] Mean: 162.6928
Treatment[10] Mean: 118.5197
Treatment[11] Mean: 189.0615
Treatment[12] Mean: 190.4608
Treatment[13] Mean: 169.4514
Treatment[14] Mean: 197.0827
Treatment[15] Mean: 185.3560
Treatment[16] Mean: 168.8029
Standard Error for Comparing Two Treatment Means: 13.221848
(df=45)
LSD Comparison: Size of Groups of Means
0
12
12
0
11
0
0
0
0
7
0
0
0
0
0
a = MACHINE(/Float)
NaN = a.NAN
; Total number of observations
n = 100
; Number of locations
n_locations = 2
; Number of treatments
n_treatments = 25
; Number of replicates
n_reps = 2
; Total number of blocks
n_blocks = 10
rep = [ $
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, $
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, $
1, 1, 1, 1, 1, 2, 2, 2, 2, 2, $
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, $
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, $
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, $
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, $
1, 1, 1, 1, 1, 2, 2, 2, 2, 2, $
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, $
2, 2, 2, 2, 2, 2, 2, 2, 2, 2 ]
block = [ $
1, 1, 1, 1, 1, 2, 2, 2, 2, 2, $
3, 3, 3, 3, 3, 4, 4, 4, 4, 4, $
5, 5, 5, 5, 5, 6, 6, 6, 6, 6, $
7, 7, 7, 7, 7, 8, 8, 8, 8, 8, $
9, 9, 9, 9, 9, 10, 10, 10, 10, 10, $
1, 1, 1, 1, 1, 2, 2, 2, 2, 2, $
3, 3, 3, 3, 3, 4, 4, 4, 4, 4, $
5, 5, 5, 5, 5, 6, 6, 6, 6, 6, $
7, 7, 7, 7, 7, 8, 8, 8, 8, 8, $
9, 9, 9, 9, 9, 10, 10, 10, 10, 10 ]
treatment = [ $
1, 2, 3, 4, 5, $
6, 7, 8, 9, 10, $
11, 12, 13, 14, 15, $
16, 17, 18, 19, 20, $
21, 22, 23, 24, 25, $
1, 6, 11, 16, 21, $
2, 7, 12, 17, 22, $
3, 8, 13, 18, 23, $
4, 9, 14, 19, 24, $
5, 10, 15, 20, 25, $
1, 2, 3, 4, 5, $
6, 7, 8, 9, 10, $
11, 12, 13, 14, 15, $
16, 17, 18, 19, 20, $
21, 22, 23, 24, 25, $
1, 6, 11, 16, 21, $
2, 7, 12, 17, 22, $
3, 8, 13, 18, 23, $
4, 9, 14, 19, 24, $
5, 10, 15, 20, 25 ]
locations = [ $
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, $
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, $
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, $
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, $
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, $
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, $
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, $
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, $
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, $
2, 2, 2, 2, 2, 2, 2, 2, 2, 2 ]
y = [$
NaN, 7, 5, 8, 6, $
16, 12, 12, 13, 8, $
17, 7, 7, 9, 14, $
18, 16, 13, 13, 14, $
14, 15, 11, 14, 14, $
24, 13, 24, 11, 8, $
21, 11, 14, 11, 23, $
16, 4, 12, 12, 12, $
17, 10, 30, 9, 23, $
15, 15, 22, 16, 19, $
13, 26, 9, 13, 11, $
15, 18, 22, 11, 15, $
19, 10, 10, 10, 16, $
21, 16, 17, 4, 17, $
15, 12, 13, 20, 8, $
16, 7, 20, 13, 21, $
15, 10, 11, 7, 14, $
7, 11, 15, 15, 16, $
19, 14, 20, 6, 16, $
17, 18, 20, 15, 14 ]
aov = LATTICE_DESIGN(n, n_locations, n_reps, n_blocks, $
n_treatments, rep, block, treatment, $
y, Locations=locations, $
Cv=cv, $
Grand_mean=grand_mean, $
Location_anova_table= $
location_anova_table, $
Treatment_means=treatment_means, $
Anova_row_labels=anova_row_labels, $
Std_err=std_err, $
N_missing=n_missing)
labels = ['Locations ', $
'Replicates within', $
' Locations' , $
'Treatments ', $
' (unadjusted)' , $
'Treatments ', $
' (adjusted)' , $
'Blocks (adjusted)', $
'Intra-Block Error', $
'Corrected Total ']
; Print Analysis of Variance Table
PRINT, " *** ANALYSIS OF VARIANCE TABLE ***"
PRINT, 'ID', 'DF', 'SSQ', 'MS', 'F-test', 'P-Value', $
Format='(A21, A7, A8, A9, A8, A8)' & $
idx = 0
FOR i=0L, (SIZE(aov))(1)-1 DO BEGIN & $
PRINT, labels(idx), aov(i,0), aov(i,1), $
aov(i,2), aov(i,3), aov(i,4), aov(i,5), Format= $
'(A17, 1X, I3, 2X, F3.0, 2X, F8.2, 2X, F7.2, 2X, ' + $
'F5.2, 2X, F7.3)' & $
idx = idx + 1 & $
IF idx LT N_ELEMENTS(labels)-1 THEN $
WHILE STRPOS(labels(idx), ' ', 0) EQ 0 DO BEGIN & $
PRINT, labels(idx) & idx = idx + 1 & $
ENDWHILE & $
ENDFOR
PRINT, ''
; Print the location ANOVA tables
idx = 0
FOR j=0L, n_locations-1 DO BEGIN & $
PRINT, "LOCATION", j, Format='(A33, 1X, I1)' & $
PRINT, "*** ANALYSIS OF VARIANCE TABLE ***", $
Format='(A47)' & $
PRINT, 'ID', 'DF', 'SSQ', 'MS', 'F-test', 'P-Value', $
Format='(A23, A5, A9, A8, A8, A8)' & $
FOR i=0L, (SIZE(aov))(1)-1 DO BEGIN & $
PRINT, labels(idx), location_anova_table(j,i,0), $
location_anova_table(j,i,1), $
location_anova_table(j,i,2), $
location_anova_table(j,i,3), $
location_anova_table(j,i,4), $
location_anova_table(j,i,5), Format= $
'(A17, 2X, I3, 3X, F3.0, 2X, F7.2, 2X, F6.2, ' + $
'2X, F5.2, 2X, F7.3)' & $
idx = idx + 1 & $
IF idx LT N_ELEMENTS(labels)-1 THEN $
WHILE STRPOS(labels(idx), ' ', 0) EQ 0 DO BEGIN & $
PRINT, labels(idx) & idx = idx + 1 & $
ENDWHILE & $
ENDFOR & $
idx = 0 & $
PRINT, '' & $
ENDFOR
PRINT, ''
PRINT, grand_mean, $
Format='("Adjusted Grand Mean :", F8.3)'PRINT, cv, Format='("Coefficient of Variation:", F8.3)'PRINT, ''
PRINT, "Adjusted Treatment Means:"
FOR i=0L, n_treatments-1 DO $
PRINT, (i+1), treatment_means(i), Format= $
"(2X, 'Treatment[', I2, '] Mean:', F10.4)"
PRINT, ''
PRINT, std_err(2), $
Format='("Standard Error for Comparing Two Treatment ' + $'Means: ", F9.6, I1)'
PRINT, FIX(std_err(3)), Format='("(df=", I2, ")")'PRINT, ''
; Perform multiple comparison using the LSD procedure
equal_means = MULTICOMP(treatment_means, std_err(3), $
std_err(2)/SQRT(2.0), $
/LSD, Alpha=0.05)
PM, equal_means, $
Title="LSD Comparison: Size of Groups of Means"
PRINT, ''
PRINT, n_missing, Format= $
'("Number of missing observations: ", I2)'*** ANALYSIS OF VARIANCE TABLE ***
ID DF SSQ MS F-test P-Value
Locations -1 1. 12.19 12.19 0.25 0.622
Replicates within -2 2. 203.99 101.99 7.44 0.001
Locations
Treatments -3 24. 795.46 33.14 0.02 1.000
(unadjusted)
Treatments -4 24. 951.20 39.63 2.89 0.006
(adjusted)
Blocks (adjusted) -5 16. 770.50 48.16 3.51 0.000
Intra-Block Error -6 55. 753.82 13.71 NaN NaN
Corrected Total -7 98. 2535.95 NaN NaN NaN
LOCATION 0
*** ANALYSIS OF VARIANCE TABLE ***
ID DF SSQ MS F-test P-Value
Locations -1 NaN NaN NaN NaN NaN
Replicates within -2 1. 203.67 203.67 NaN NaN
Locations
Treatments -3 24. 567.13 23.63 0.78 0.721
(unadjusted)
Treatments -4 24. 661.08 27.54 2.04 0.078
(adjusted)
Blocks (adjusted) -5 8. 490.51 61.31 NaN NaN
Intra-Block Error -6 15. 202.93 13.53 NaN NaN
Corrected Total -7 48. 1464.24 NaN NaN NaN
LOCATION 1
*** ANALYSIS OF VARIANCE TABLE ***
ID DF SSQ MS F-test P-Value
Locations -1 NaN NaN NaN NaN NaN
Replicates within -2 1. 0.32 0.32 NaN NaN
Locations
Treatments -3 24. 622.52 25.94 1.43 0.196
(unadjusted)
Treatments -4 24. 707.51 29.48 2.83 0.018
(adjusted)
Blocks (adjusted) -5 8. 269.76 33.72 NaN NaN
Intra-Block Error -6 16. 166.92 10.43 NaN NaN
Corrected Total -7 49. 1059.52 NaN NaN NaN
Adjusted Grand Mean : 14.011
Coefficient of Variation: 26.423
Adjusted Treatment Means:
Treatment[ 1] Mean: 17.1507
Treatment[ 2] Mean: 19.2200
Treatment[ 3] Mean: 11.1261
Treatment[ 4] Mean: 14.6230
Treatment[ 5] Mean: 12.6543
Treatment[ 6] Mean: 11.8133
Treatment[ 7] Mean: 11.9045
Treatment[ 8] Mean: 11.3106
Treatment[ 9] Mean: 9.5576
Treatment[10] Mean: 11.5889
Treatment[11] Mean: 22.1320
Treatment[12] Mean: 12.7232
Treatment[13] Mean: 13.1293
Treatment[14] Mean: 17.8763
Treatment[15] Mean: 18.6576
Treatment[16] Mean: 14.6568
Treatment[17] Mean: 11.4980
Treatment[18] Mean: 13.1540
Treatment[19] Mean: 5.4010
Treatment[20] Mean: 12.9323
Treatment[21] Mean: 15.4108
Treatment[22] Mean: 17.0020
Treatment[23] Mean: 13.9081
Treatment[24] Mean: 17.6550
Treatment[25] Mean: 13.1864
Standard Error for Comparing Two Treatment Means: 4.617282
(df=55)
LSD Comparison: Size of Groups of Means
16
22
22
0
0
0
0
0
0
0
15
0
0
0
0
0
0
0
0
0
0
0
0
0
Number of missing observations: 1