ANOVAFACT Function (PV-WAVE Advantage)

IMSL Statistics Reference Guide > Analysis of Variance and Designed Experiments > ANOVAFACT Function (PV-WAVE Advantage)

Analyzes a balanced factorial design with fixed effects.

Usage

result = ANOVAFACT(n_levels, y)

Input Parameters

n_levels—One-dimensional array containing the number of levels for each of the factors and the number of replicates for each effect.

y—One-dimensional array of length:

n_levels (0) * n_levels (1) * ... * ((N_ELEMENTS (n_levels) – 1))

containing the responses. Parameter y must not contain NaN for any of its elements, i.e., missing values are not allowed.

Returned Value

result—The p-value for the overall F-test.

Input Keywords

Double—If present and nonzero, then double precision is used.

Order—Number of factors included in the highest-way interaction in the model. Order must be in the interval [1, N_ELEMENTS (n_levels) – 1]. For example, an Order of 1 indicates that a main-effect model is analyzed, and an Order of 2 indicates that two-way interactions are included in the model. Default: Order = N_ELEMENTS(n_levels) – 1)

Pure_Error, Pool_Inter—If present and nonzero, Pure_Error (the default option) indicates all the main effect and the interaction effects involving the replicates, the last element in n_levels, are pooled together to create the error term. The Pool_Inter option indicates (Order + 1)-way and higher-way interactions are pooled together to create the error. Keywords Pure_Error and Pool_Inter cannot be used together.

Output Keywords

Anova_Table—Named variable into which an array of size 15 containing the analysis of variance table is stored. The analysis of variance statistics are given as follows:

0—degrees of freedom for the model

1—degrees of freedom for error

2—total (corrected) degrees of freedom

3—sum of squares for the model

4—sum of squares for error

5—total (corrected) sum of squares

6—model mean square

7—error mean square

8—overall F-statistic

9—p-value

10—R2 (in percent)

11—adjusted R2 (in percent)

12—estimate of the standard deviation

13—overall mean of y

14—coefficient of variation (in percent)

Test_Effects—Named variable into which an array of size nef × 4 containing statistics relating to the sums of squares for the effects in the model is stored. Here:

where n is given by N_ELEMENTS(n_levels) if Pool_Inter is specified; otherwise, N_ELEMENTS(n_levels) – 1.

Suppose the factors are A, B, C, and error. With Order = 3, rows 0 through nef – 1 correspond to A, B, C, AB, AC, BC, and ABC. The columns of Test_Effects are as follows:

0—degrees of freedom

1—sum of squares

2—F-statistic

3—p-value

Means—Named variable into which an array of length (n_levels(0) + 1) × (n_levels(1) + 1) × ... × (n_levels(n–1) + 1) containing the subgroup means is stored.

See keyword Test_Effects for a definition of n. If the factors are A, B, C, and replicates, the ordering of the means is grand mean, A means, B means, C means, AB means, AC means, BC means, and ABC means.

Discussion

Function ANOVAFACT performs an analysis for an n-way classification design with balanced data. For balanced data, there must be an equal number of responses in each cell of the n-way layout. The effects are assumed to be fixed effects. The model is an extension of the two-way model to include n factors. The interactions (two-way, three-way, up to n-way) can be included in the model, or some of the higher-way interactions can be pooled into error. The keyword Order specifies the number of factors to be included in the highest-way interaction. For example, if three-way and higher-way interactions are to be pooled into error, set Order = 2.

By default, Order = N_ELEMENTS (n_levels) – 1 with the last subscript being the replicates subscript. Keyword Pure_Error indicates there are repeated responses within the n-way cell; Pool_Inter indicates otherwise.

Function ANOVAFACT requires the responses as input into a single vector y in lexicographical order, so that the response subscript associated with the first factor varies least rapidly, followed by the subscript associated with the second factor, and so forth. Hemmerle (1967, Chapter 5) discusses the computational method.

Example 1

A two-way analysis of variance is performed with balanced data discussed by Snedecor and Cochran (1967, Table 12.5.1, p. 347). The responses are the weight gains (in grams) of rats that were fed diets varying in the source (A) and level (B) of protein.

The model is:

for

;

where:

for

for i = 0, 1. The first responses in each cell in the two-way layout are given in Cell First Responses:

Table 5-24: Cell First Responses
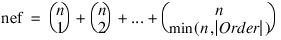
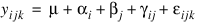
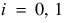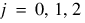Protein Level (B)	Protein Source (A)
Protein Level (B)	Beef	Cereal	Pork
High	73, 102, 118, 104, 81, 107, 100, 87, 117, 111	98, 74, 56, 111, 95, 88, 82, 77, 86, 92	94, 79, 96, 98, 102, 102, 108, 91, 120, 105
Low	90, 76, 90, 64, 86, 51, 72, 90, 95, 78	107, 95, 97, 80, 98, 74, 74, 67, 89, 58	49, 82, 73, 86, 81, 97, 106, 70, 61, 82

n = [3, 2, 10]

y = [73.0, 102.0, 118.0, 104.0,  81.0, 107.0, 100.0,  87.0, $

   117.0, 111.0, 90.0,  76.0,  90.0,  64.0,  86.0, 51.0,  72.0, $

   90.0,  95.0,  78.0, 98.0,  74.0,  56.0, 111.0,  95.0, 88.0, $

   82.0, 77.0,  86.0,  92.0, 107.0,  95.0,  97.0,  80.0,  98.0, $

   74.0,  74.0,  67.0,  89.0,  58.0, 94.0,  79.0,  96.0,  98.0, $

   102.0, 102.0, 108.0, 91.0, 120.0, 105.0, 49.0,  82.0,  73.0, $

   86.0,  81.0, 97.0, 106.0, 70.0,  61.0,  82.0]

p_value = ANOVAFACT(n, y, Anova_Table = anova_table)

PRINT, 'p-value = ', p_value

; PV-WAVE prints: p-value =    0.00229943

Example 2: Two-way ANOVA

In this example, the same model and data are fit as in the initial example, but keywords are used for a more complete analysis. First, a procedure to output the results is defined.

PRO print_results, anova_table, test_effects, means

   anova_labels = ['df for among groups', $

      'df for within groups', 'total (corrected) df', $

      'ss for among groups', 'ss for within groups', $

      'total (corrected) ss', 'mean square among groups', $

      'mean square within groups', 'F-statistic', $

      'P-value', 'R-squared (in percent)', $

      'adjusted R-squared (in percent)', $

      'est. std of within group error', 'overall mean of y', $

      'coef. of variation (in percent)']

   effects_labels = ['A  ', 'B  ', 'A*B']

   means_labels = ['grand', 'A1', 'A2', $

      'A3', 'B1', 'B2', 'A1*B1', 'A1*B2', $

      'A2*B1', 'A2*B2', 'A3*B1', 'A3*B2']

   PRINT, '       * *Analysis of Variance * *'

   FOR i=0L, 14 DO PM, anova_labels(i), $

      anova_table(i), Format = '(a40,f15.2)'

   PRINT

   ; Print the analysis of variance table.

   PRINT, '     * * Variation Due to the Model * *'

   PRINT, 'Source    DF      SS      MS      P-value'

   FOR i=0L, 2 DO PM, effects_labels(i), test_effects(i, *)

   PRINT

   PRINT, ' * * Subgroup Means * *'

   FOR i=0L, 11 DO PM, means_labels(i), $

      means(i), Format = '(a5,f15.2)'

END

n = [3, 2, 10]

y = [73.0, 102.0, 118.0, 104.0,  81.0, 107.0, 100.0,  87.0, $

   117.0, 111.0, 90.0,  76.0,  90.0,  64.0,  86.0, 51.0,  72.0, $

   90.0,  95.0,  78.0, 98.0,  74.0,  56.0, 111.0,  95.0, 88.0, $

   82.0,  77.0,  86.0,  92.0, 107.0,  95.0,  97.0,  80.0, 98.0, $

   74.0,  74.0,  67.0,  89.0,  58.0, 94.0,  79.0,  96.0,  98.0, $

   102.0, 102.0, 108.0,  91.0, 120.0, 105.0, 49.0,  82.0, 73.0, $

   86.0,  81.0, 97.0, 106.0,  70.0,  61.0,  82.0]

p_value = ANOVAFACT(n, y, Anova_Table = anova_table, $

   Test_Effects = test_effects, Means = means)

print_results, anova_table, test_effects, means

This results in the following output:

* *Analysis of Variance * *

df for among groups                     5.00

df for within groups                   54.00

total (corrected) df                   59.00

ss for among groups                  4612.93

ss for within groups                11586.00

total (corrected) ss                16198.93

mean square among groups              922.59

mean square within groups             214.56

F-statistic                             4.30

P-value                                 0.00

R-squared (in percent)                 28.48

adjusted R-squared (in percent)        21.85

est. std of within group error         14.65

overall mean of y                      87.87

coef. of variation (in percent)        16.67

 * * Variation Due to the Model * * 
Source      DF      SS        MS       P-value
A       2.00000  266.533   0.621128  0.541132 
B       1.00000  3168.27  14.7667    0.000322342
A*B     2.00000  1178.13   2.74552   0.0731880

 * * Subgroup Means * *

grand          87.87

 A1            89.60

 A2            84.90

 A3            89.10

 B1            95.13

 B2            80.60

A1*B1         100.00

A1*B2          79.20

A2*B1          85.90

A2*B2          83.90

A3*B1          99.50

A3*B2          78.70

Example 3: Three-way ANOVA

This example performs a three-way analysis of variance using data discussed by John (1971, pp. 91–92). The responses are weights (in grams) of roots of carrots grown with varying amounts of applied nitrogen (A), potassium (B), and phosphorus (C). Each cell of the three-way layout has one response. Note that the ABC interactions sum of squares (186) is given incorrectly by John (1971, Table 5.2.)

The three-way layout is given in Three-way Layout:

Table 5-25: Three-way Layout
	A0			A1			A2
	B0	B1	B2	B0	B1	B2	B0	B1	B2
C0	88.76	91.41	97.85	94.83	100.49	99.75	99.90	100.23	104.51
C1	87.45	98.27	95.85	84.57	97.20	112.30	92.98	107.77	110.94
C2	86.01	104.20	90.09	81.06	120.80	108.77	94.72	118.39	102.87

PRO print_results, anova_table, test_effects, means

   anova_labels = ['df for among groups', $

      'df for within groups', 'total (corrected) df', $

      'ss for among groups', 'ss for within groups', $

      'total (corrected) ss', 'mean square among groups', $

      'mean square within groups', 'F-statistic', $

      'P-value', 'R-squared (in percent)', $

      'adjusted R-squared (in percent)', $

      'est. std of within group error', $

      'overall mean of y', 'coef. of variation (in percent)']

   effects_labels = ['A  ', 'B  ', 'C  ', 'A*B', 'A*B', 'A*C']

   PRINT, '       * *Analysis of Variance * *'

   FOR i=0L, 14 DO PM, anova_labels(i), $

      anova_table(i), Format = '(a40,f15.2)'

   PRINT

   PRINT, '     * * Variation Due to the Model * *'

   PRINT, 'Source      DF     SS       MS     P-value'

   FOR i=0L,5 DO PM, effects_labels(i), test_effects(i, *)

END

n = [3, 3, 3]

y = [88.76, 87.45, 86.01, 91.41, 98.27, 104.20, 97.85, $

   95.85, 90.09, 94.83, 84.57, 81.06, 100.49, 97.20, $

   120.80, 99.75, 112.30, 108.77, 99.90, 92.98, 94.72, $

   100.23, 107.77, 118.39, 104.51, 110.94, 102.87]

p_value = ANOVAFACT(n, y, Anova_Table = anova_table, $

   Test_Effects = test_effects, /Pool_Inter)

print_results, anova_table, test_effects

This results in the following output:

* *Analysis of Variance * *

df for among groups                    18.00

df for within groups                    8.00

total (corrected) df                   26.00

ss for among groups                  2395.73

ss for within groups                  185.78

total (corrected) ss                 2581.51

mean square among groups              133.10

mean square within groups              23.22

F-statistic                             5.73

p-value                                 0.01

R-squared (in percent)                 92.80

adjusted R-squared (in percent)        76.61

est. std of within group error          4.82

overall mean of y                      98.96

coef. of variation (in percent)         4.87

 * * Variation Due to the Model * *

Source   DF      SS         MS       p-value

A    2.00000   488.368    10.5152    0.00576699

B    2.00000  1090.66     23.4832    0.000448704

C    2.00000    49.1484    1.05823   0.391063

A*B  4.00000   142.586     1.53502   0.280423

A*B  4.00000    32.3474    0.348241  0.838336

A*C  4.00000   592.624     6.37997   0.0131252

Version 2017.0