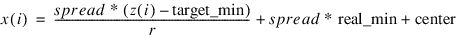SCALE_FILTER Function (PV-WAVE Advantage)
Scales or unscales continuous data prior to its use in neural network training, testing, or forecasting.
Usage
result = SCALE_FILTER(x, method)
Input Parameters
x—An array of length n_obs, where n_obs is the number of observations. The values in x are either the scaled or unscaled values of a continuous variable. Missing values cannot be omitted. They are indicated by placing a NaN (Not a Number) at the appropriate positions in x. NaN can be defined by calling the MACHINE function. For example:
mach = MACHINE(/Float)
x(i) = mach.NaN
method—The scaling method to apply to each variable. The sign of
method determines whether the values in
x are scaled or unscaled. If
method is positive then values in
x are scaled. If
method is negative then values in
x are unscaled. The association of the value in
method and the scaling algorithm is summarized in
Method Scaling Algorithm.
Returned Value
result—Array of length n_obs containing either the scaled or unscaled value of x, depending upon whether method is positive or negative, respectively.
Input Keywords
Double—If present and nonzero, double precision is used.
Scale_limits—A four element array (real_min, real_max, target_min, target_max) representing the real and target limits for x. This keyword is required when bounded scaling is performed, i.e., method = ±1, ±4, or ±5. real_min is the lowest value expected for each input variable in x. real_max is the largest value expected. target_min is the lowest value allowed for the output variable, result. target_max is the largest value allowed for the output variable.
Supply_center_spread—Two element array (center, spread). The values center and spread are only used for z-score scaling or unscaling of x, that is, when method is ±2, ±3, ±4, or ±5. The value of center is either the mean or median, and the value of spread is either the standard deviation or mean absolute difference. When method is positive, this keyword can be used to supply a user-defined center and spread rather than allowing SCALE_FILTER to compute the center and spread from the data in x. When method is –2, –3, –4, or –5, this optional keyword must be used to supply the center and spread used during scaling.
Output Keywords
Return_center_spread—A two element array (center, spread). The values center and spread are only used for z-score scaling or unscaling of x using methods ±2, ±3, ±4, or ±5. The value of center is either the mean or median for x. The value of spread is either the standard deviation or mean absolute difference for x.
Discussion
SCALE_FILTER is designed to either scale or unscale a continuous variable using one of four methods prior to their use as neural network input or output.
The specific encoding computations employed are specified by the method parameter. Scaling limits are supplied with the Scale_limits keyword, and are required for the bounded scaling methods, i.e., method = ±1, ±4, or ±5. Bounded scaling ensures that the scaled values in the returned array fall between a lower and upper bound.
If method = 1 then the bounded method of scaling and unscaling is applied to x using the scaling limits.
If method = ±2, ±3, ±4, or ±5, then the z-score method of scaling is used. These calculations are based upon the following scaling calculation:
where a is a measure of center for x, and b is a measure of the spread of x.
If method = ±2 or ±4, then by default a and b are the arithmetic average and sample standard deviation of the training data. These values can be overridden using the keyword Supply_center_spread.
If
method = ±3 or ±5, then by default
a and
b are the median and
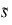
, where
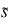
is a robust estimate of the population standard deviation:
Again, the values of a and b can be overridden using the keyword Supply_center_spread.
Method ±1: Bounded Scaling and Unscaling
If method = 1, then the Scale_limits keyword is required and a scaling operation is conducted using the scale limits for x using the following calculation:
where:
If method = –1, then the Scale_limits keyword is required and an unscaling operation is conducted by inverting the following calculation:
Method +2 or +3: Unbounded z-score Scaling
If method = 2 or method = 3, then a scaling operation is conducted using the scale limits of x using a z-score calculation:
If either
center or
spread are missing, (a NaN), then appropriate values are calculated from the non-missing values of
x. If
method = 2, then
center is set equal to the arithmetic average
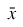
, and
spread is set equal to the sample standard deviation,
s.
If
method = 3, then
center is set equal to the median
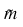
, and
center is set equal to the Mean Absolute Difference (MAD).
Method -2 or -3: Unbounded z-score Unscaling
If
method = –2 or
method = –3, then an unscaling operation is conducted using the inverse calculation for the equation shown in
Method +2 or +3: Unbounded z-score Scaling:
For these values of method, missing values for center and spread are not allowed. If method = –2, then center and spread are assumed to be equal to the arithmetic average and standard deviation, respectively. These values would normally be the same used in scaling the variable with method = +2. If method = –3, then center and spread are assumed to be equal to the median and mean absolute difference, respectively. These values would normally be the same used in scaling the variable with method = +3.
Method +4 or +5: Bounded z-score Scaling
This method is essentially the same as the z-score calculation described for method = +2 and method = +3 with additional scaling or unscaling using the scale limits. If method = 4, then the Scale_limits keyword is required and a scaling operation is conducted using the scale limits for x using the widely known z-score calculation:
If either
center or
spread are missing, (a NaN), then appropriate values are calculated from the non-missing values in
x. If
center is missing and
method = +4, then
center is set equal to the arithmetic average
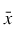
, and
spread is set equal to the Sample Standard Deviation,
s. If
center is missing and
method = +5, then
center(i) is set equal to the median
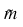
, and
spread is set equal to the MAD.
In bounded scaling, if z(i) exceeds its bounds, it is set to the boundary it exceeded.
Method -4 or -5: Bounded z-score unscaling
If method = –4 or method = –5, then the Scale_limits keyword is required and an unscaling operation is conducted using the inverse calculation for the equation:
For these values of method, missing values for center and spread are not allowed. If method = –4, then center and spread are assumed to be equal to the arithemetic average and standard deviation, respectively. These values would normally be the same used in scaling x with method = +4. If method = –5, then center and spread are assumed to be equal to the median and mean absolute difference, respectively. These values would normally be the same used in scaling the x with method = +5.
Example
In this example two data sets with five observations are filtered using bounded z-score scaling.
; First data set.
x1 = [3.5, 2.4, 4.4, 5.6, 1.1]
z1 = SCALE_FILTER( x1, 4, Scale_limits=[-6.0,6.0,-3.0,3.0], $
Return_center_spread=rcs)
y1 = SCALE_FILTER( z1, -4, Scale_limits=[-6.0,6.0,-3.0,3.0], $
Supply_center_spread=rcs)
center1 = rcs(0)
spread1 = rcs(1)
PM, z1, Title = "Z1"
PRINT, " Center = ", center1, Format='(A11, F8.6)'
PRINT, " Spread = ", spread1, Format='(A11, F8.6)'
PRINT, ""
; Second data set.
x2 = [3.1, 1.5, -1.5, 2.4, 4.2]
z2 = SCALE_FILTER( x2, 5, Scale_limits=[-3.0,3.0,-3.0,3.0], $
Return_center_spread=rcs2)
y2 = SCALE_FILTER( z2, -5, Scale_limits=[-3.0,3.0,-3.0,3.0], $
Supply_center_spread=rcs2)
center2 = rcs2(0)
spread2 = rcs2(1)
; Print outputs
PM, z2, Title = "Z2"
PRINT, " Center = ", center2, Format='(A11, F8.6)'
PRINT, " Spread = ", spread2, Format='(A11, F8.6)'
PRINT, ""
PM, y1, Title = "Y1"
PRINT, ""
PM, y2, Title = "Y2"
Output
Z1
0.0287006
-0.287006
0.287006
0.631413
-0.660113
Center = 3.400000
Spread = 1.742125
Z2
0.524603
-0.674490
-2.92279
0.00000
1.34898
Center = 2.400000
Spread = 1.334342
Y1
3.50000
2.40000
4.40000
5.60000
1.10000
Y2
3.10000
1.50000
-1.50000
2.40000
4.20000
Version 2017.0
Copyright © 2017, Rogue Wave Software, Inc. All Rights Reserved.
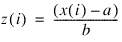
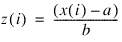
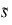 , where
, where 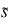 is a robust estimate of the population standard deviation:
is a robust estimate of the population standard deviation: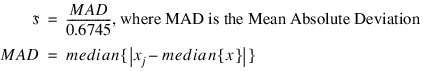
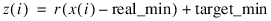
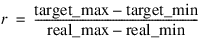
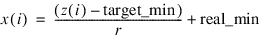
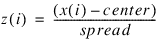
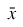 , and spread is set equal to the sample standard deviation, s.
, and spread is set equal to the sample standard deviation, s.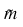 , and center is set equal to the Mean Absolute Difference (MAD).
, and center is set equal to the Mean Absolute Difference (MAD).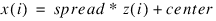
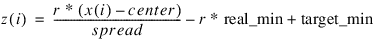
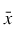 , and spread is set equal to the Sample Standard Deviation, s. If center is missing and method = +5, then center(i) is set equal to the median
, and spread is set equal to the Sample Standard Deviation, s. If center is missing and method = +5, then center(i) is set equal to the median 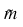 , and spread is set equal to the MAD.
, and spread is set equal to the MAD.