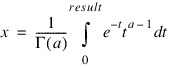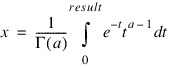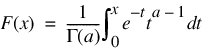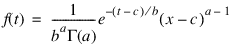GAMMACDF Function (PV-WAVE Advantage)
Evaluates the gamma distribution function.
Usage
result = GAMMACDF(x, a)
Input Parameters
x—Argument for which the gamma distribution function is to be evaluated.
a—Shape parameter of the gamma distribution. This parameter must be positive.
Returned Value
result—The probability that a gamma random variable takes a value less than or equal to x.
Input Keywords
Double—If present and nonzero, double precision is used.
Inverse—If present and nonzero, evaluates the inverse distribution function of a gamma random variable with shape parameter a. x is now the probability for which the inverse gamma distribution is to be evaluated, with x in the open interval (0.0, 1.0), and result is such that:
where Γ(⋅) is the gamma function. The probability that the random variable takes a value less than or equal to result is x.
The inverse of the gamma distribution function uses bisection and modified regula falsi to invert the distribution function, which is evaluated using the GAMMACDF function.
Discussion
Function GAMMACDF evaluates the distribution function, F, of a gamma random variable with shape parameter a; that is:
where Γ(·) is the gamma function. (The gamma function is the integral from 0 to infinity of the same integrand as above.) The value of the distribution function at the point x is the probability that the random variable takes a value less than or equal to x.
The gamma distribution is often defined as a two-parameter distribution with a scale parameter b (which must be positive) or even as a three-parameter distribution in which the third parameter c is a location parameter. In the most general case, the probability density function over (c, infinity) is as follows:
If T is such a random variable with parameters a, b, and c, the probability that T ≤ t0 can be obtained from GAMMACDF by setting x = (t0 – c ) / b.
If x is less than a or if x is less than or equal to 1.0, GAMMACDF uses a series expansion; otherwise, a continued fraction expansion is used. (See Abramowitz and Stegun, 1964.)
Example 1
Let X be a gamma random variable with a shape parameter of 4. (In this case, it has an Erlang distribution, since the shape parameter is an integer.) This example finds the probability that X is less than 0.5 and the probability that X is between 0.5 and 1.0.
a = 4
x = .5
p = GAMMACDF(x, a)
PM, p, Title = 'The probability that X is less ' + $
'than .5 is:'
; PV-WAVE prints the following:
; The probability that X is less than .5 is: 0.00175162
x = 1
p = GAMMACDF(x, a) - p
PM, p, Title = 'The probability that X is between .5 and 1 is:'
; PV-WAVE prints the following:
; The probability that X is between .5 and 1 is: 0.0172365
Example 2
This exmaple demonstrates the use of the GAMMACDF with the Inverse keyword
p = GAMMACDF(.95, 4, Double=itype, /Inverse)
p_out = STRING(p, Format='(F6.4)')
PRINT,"The 0.05 gamma(4) critical value is "+p_out
; PV-WAVE prints the following:
; The 0.05 gamma(4) critical value is 7.7537
Informational Errors
STAT_LESS_THAN_ZERO—Input argument, x, is less than zero.
Fatal Errors
STAT_X_AND_A_TOO_LARGE—Function overflows because x and a are too large.
Version 2017.0
Copyright © 2017, Rogue Wave Software, Inc. All Rights Reserved.