POISSONCDF Function (PV-WAVE Advantage)
Evaluates the Poisson distribution function.
Usage
result = POISSONCDF(k, theta)
Input Parameters
k—Parameter for which the Poisson distribution function is to be evaluated.
theta—Mean of the Poisson distribution. Parameter theta must be positive.
Returned Value
result—The probability that a Poisson random variable takes a value less than or equal to k.
Input Keywords
Double—If present and nonzero, double precision is used.
Discussion
Function POISSONCDF evaluates the distribution function of a Poisson random variable with parameter theta. The mean of the Poisson random variable, theta, must be positive.
The probability function (with θ = theta) is as follows:
The individual terms are calculated from the tails of the distribution to the mode of the distribution and summed. The POISSONCDF function uses the recursive relationship:
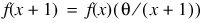
,
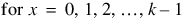
with
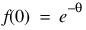
.
Example
Suppose X is a Poisson random variable with θ = 10. This example evaluates the probability that X ≤ 7.
p = POISSONCDF(7, 10)
PM, 'Pr(x <= 7) = ', p, Format = '(a13,f7.4)'
; PV-WAVE prints: Pr(x <= 7) = 0.2202
Informational Errors
STAT_LESS_THAN_ZERO— Input parameter, k, is less than zero.
Version 2017.0
Copyright © 2017, Rogue Wave Software, Inc. All Rights Reserved.
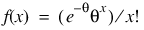
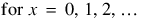
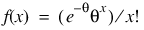
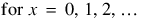
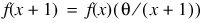 ,
, 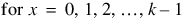
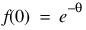 .
.