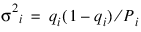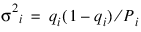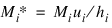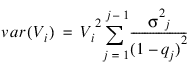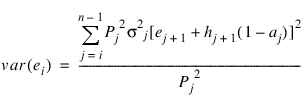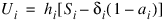LIFE_TABLES Function (PV-WAVE Advantage)
Produces population and cohort life tables.
Usage
result = LIFE_TABLES (age, a, n_cohort)
Input Parameters
age—Array of length n_classes + 1, where n_classes is the number of age classes containing the lowest age in each age interval, and in age(n_classes), the endpoint of the last age interval. Negative age(0) indicates that the age intervals are all of length |age(0)| and that the initial age interval is from 0.0 to |age(0)|. In this case, all other elements of age need not be specified. age(n_classes) need not be specified when getting a cohort table.
a—Array of length n_classes containing the fraction of those dying within each interval who die before the interval midpoint. A common choice for all a(i) is 0.5. This choice may also be specified by setting a(0) to any negative value. In this case, the remaining values of a need not be specified.
n_cohort—Array of length n_classes containing the cohort sizes during each interval. If the N_deaths keyword is used, then n_cohort(i) contains the size of the population at the midpoint of interval i. Otherwise, n_cohort(i) contains the size of the cohort at the beginning of interval i. When requesting a population table, the population sizes in n_cohort may need to be adjusted to correspond to the number of deaths in N_deaths.
Returned Value
result—Array of length
n_classes by 12 containing the life table. The function returns a cohort table by default. If the
N_deaths keyword is used, a population table is returned. Entries in the
ith row are for the age interval defined by
age(
i). Column definitions are described in
Population Table Column Definitions.
Input Keywords
Double—If present and nonzero, double precision is used.
Population_size—The population size at the beginning of the first age interval in requesting population table. A default value of 10,000 is used to allow easy entry of n_cohorts and N_deaths when numbers are available as percentages. Default: Population_size = 10000.
N_deaths—Array of length n_classes containing the number of deaths in each age interval.
Discussion
LIFE_TABLES computes population (current) or cohort life tables based upon the observed population sizes at the middle (for population table) or the beginning (for cohort table) of some userspecified age intervals. The number of deaths in each of these intervals must also be observed.
The probability of dying prior to the middle of the interval, given that death occurs somewhere in the interval, may also be specified. Often, however, this probability is taken to be 0.5. For a discussion of the probability models underlying the life table here, see the references.
Let ti, for i = 0, 1, ..., tn denote the time grid defining the n age intervals, and note that the length of the age intervals may vary. Following Gross and Clark (1975, page 24), let di denote the number of individuals dying in age interval i, where age interval i ends at time ti. For population table, the death rate at the middle of the interval is given by ri = di/(Mihi), where Mi is the number of individuals alive at the middle of the interval, and hi = ti – ti – 1, t0 = 0. The number of individuals alive at the beginning of the interval may be estimated by Pi = Mi + (1 - ai)di where ai is the probability that an individual dying in the interval dies prior to the interval midpoint. For cohort table, Pi is input directly while the death rate in the interval, ri, is not needed.
The probability that an individual dies during the age interval from ti – 1 to ti is given by qi = di/Pi. It is assumed that all individuals alive at the beginning of the last interval die during the last interval. Thus, qn = 1.0. The asymptotic variance of qi can be estimated by:
For population table, the number of individuals alive in the middle of the time interval (input in n_cohort(i)) must be adjusted to correspond to the number of deaths observed in the interval. LIFE_TABLES assumes that the number of deaths observed in interval hi occur over a time period equal to hi. If di is measured over a period ui, where ui ≠ di, then n_cohort(i) must be adjusted to correspond to di by multiplication by ui/hi, i.e., the value Mi input into LIFE_TABLES as n_cohort(i) is computed as:
Let Si denote the number of survivors at time ti from a hypothetical (for population table) or observed (for cohort table) population. Then, S0 = Population_size for population table, and S0 = n_cohort(0) for cohort table, and Si is given by Si = Si – 1 – δi – 1 where δi = Siqi is the number of individuals who die in the ith interval. The proportion of survivors in the interval is given by Vi = Si/S0 while the asymptotic variance of Vi can be estimated as follows:
The expected lifetime at the beginning of the interval is calculated as the total lifetime remaining for all survivors alive at the beginning of the interval divided by the number of survivors at the beginning of the interval. If ei denotes this average expected lifetime, then the variance of ei can be estimated as (see Chiang 1968):
where var(en) = 0.0.
Finally, the total number of time units lived by all survivors in the time interval can be estimated as:
Example
This example is taken from Chiang (1968). The cohort life table has thirteen equally spaced intervals, so age(0) is set to –5.0. Similarly, the probabilities of death prior to the middle of the interval are all taken to be 0.5, so a(0) is set to –1.0.
n_classes = 13 ; Number of age classes
; An array containing the lowest age in each age interval
age = FLTARR(n_classes + 1)
; Array containing the fraction of those dying within each
; interval
a = FLTARR(n_classes)
age(0) = -5.0
a(0) = -1.0
; Array of length n_classes containing the cohort sizes during
; each interval.
n_cohort = [270, 268, 264, 261, 254, 251, $
248, 232, 166, 130, 76, 34, 13]
n = MACHINE(/Float)
NaN = n.NAN
; Call the routine
result = LIFE_TABLES(age, a, n_cohort)
; Print the output
PRINT,"Age Class Age PDHALF Alive" + $
" Deaths Death Rate"
FOR i=0L,n_classes - 1 DO $
PRINT, i+1, result(i,0),result(i,1),result(i,2), $
result(i,3),result(i,4), $
Format = '(I8, I11, F11.1, 2I11, F11.1)'
PRINT,""
PRINT,"Age Class P(D) Std(P(D)) P(S) " + $
"Std(P(S)) Lifetime"
FOR i=0L,n_classes - 1 DO $
PRINT, i+1, result(i,5),result(i,6),result(i,7), $
result(i,8), result(i,9), Format = '(I8, 4F11.6, F11.2)'
PRINT,""
PRINT, "Age Class Std(Life) Time Units"
FOR i=0L,n_classes - 1 DO $
PRINT, i+1, result(i,10),result(i,11), $
Format = '(I8, F11.6, F11.1)'
Output
Age Class Age PDHALF Alive Deaths Death Rate
1 0 0.5 270 2 NaN
2 5 0.5 268 4 NaN
3 10 0.5 264 3 NaN
4 15 0.5 261 7 NaN
5 20 0.5 254 3 NaN
6 25 0.5 251 3 NaN
7 30 0.5 248 16 NaN
8 35 0.5 232 66 NaN
9 40 0.5 166 36 NaN
10 45 0.5 130 54 NaN
11 50 0.5 76 42 NaN
12 55 0.5 34 21 NaN
13 60 0.5 13 13 NaN
Age Class P(D) Std(P(D)) P(S) Std(P(S)) Lifetime
1 0.007407 0.005218 1.000000 0.000000 43.19
2 0.014925 0.007407 0.992593 0.005218 38.49
3 0.011364 0.006523 0.977778 0.008971 34.03
4 0.026820 0.010000 0.966667 0.010924 29.40
5 0.011811 0.006779 0.940741 0.014369 25.14
6 0.011952 0.006859 0.929630 0.015566 20.41
7 0.064516 0.015600 0.918518 0.016649 15.62
8 0.284483 0.029621 0.859259 0.021164 11.53
9 0.216867 0.031986 0.614815 0.029616 10.12
10 0.415385 0.043220 0.481481 0.030408 7.23
11 0.552632 0.057035 0.281481 0.027369 5.59
12 0.617647 0.083342 0.125926 0.020191 4.41
13 1.000000 0.000000 0.048148 0.013028 2.50
Age Class Std(Life) Time Units
1 0.699287 1345.0
2 0.670739 1330.0
3 0.623031 1312.5
4 0.594008 1287.5
5 0.540284 1262.5
6 0.523672 1247.5
7 0.514854 1200.0
8 0.498153 995.0
9 0.460167 740.0
10 0.432796 515.0
11 0.436072 275.0
12 0.416709 117.5
13 0.000000 32.5
Version 2017.0
Copyright © 2017, Rogue Wave Software, Inc. All Rights Reserved.