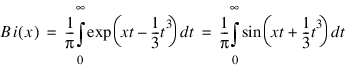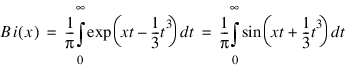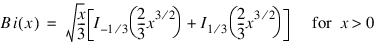AIRY_BI Function (PV-WAVE Advantage)
Evaluates the Airy function of the second kind.
Usage
result = AIRY_BI(x)
Input Parameters
x—Argument for which the function value is desired.
Returned Value
result—The value of the Airy function evaluated at x, Bi(x).
Input Keywords
Double—If present and nonzero, double precision is used.
Derivative—If present and nonzero, then the derivative of the Airy function of the second kind is computed.
Discussion
The airy function Bi(x) is defined to be:
It can also be expressed in terms of modified Bessel functions of the first kind,
Iv(
x), and Bessel functions of the first kind
Jv(
x) (see the
BESSI Function (PV-WAVE Advantage), and the
BESSJ Function (PV-WAVE Advantage)):
and:
Here ε is the machine precision. If x < −1.31ε–2/3, then the answer will have no precision. If x < −1.31ε–1/3, the answer will be less accurate than half precision. In addition, x should not be so large that exp[(2/3)x3/2] overflows.
If the keyword
Derivative is set, the airy function
Bi'(
x) is defined to be the derivative of the Airy function of the second kind,
Bi(
x) (see the
AIRY_BI Function (PV-WAVE Advantage)). If
x <
−1.31
ε–2/3, then the answer will have no precision. If
x <
−1.31
ε–1/3, the answer will be less accurate than half precision. Here
ε is the machine precision. In addition,
x should not be so large that
exp[(2/3)
x3/2] overflows.
Example
In this example, Bi(–4.9) and Bi'(–4.9) are evaluated.
PRINT, AIRY_BI(-4.9)
; PV-WAVE prints: -0.0577468
PRINT, AIRY_BI(-4.9, /Derivative)
; PV-WAVE prints: 0.827219
Version 2017.0
Copyright © 2017, Rogue Wave Software, Inc. All Rights Reserved.