Tree Layout
In this section, you will learn about the
Tree Layout algorithm provided with the Rogue Wave® Views Graph Layout package (class
IlvTreeLayout from the library
ilvtree).
Samples
Here are some sample drawings produced with the Tree Layout:
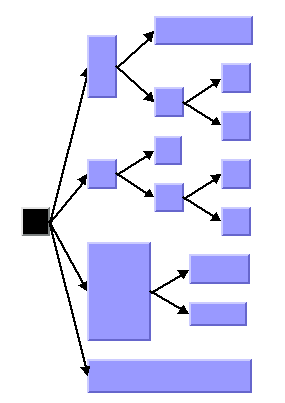
Sample Tree Layout in Free Layout Mode with Center Alignment and Flow Direction to the Right
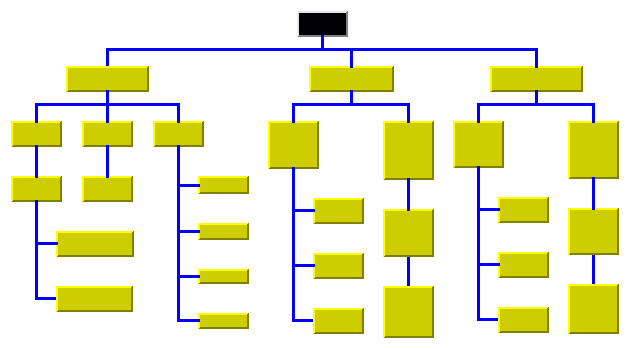
Sample Tree Layout with Flow Direction to the Bottom, Orthogonal Link Style, and Tip-Over Alignment at Some Leaf Nodes
Sample Tree Layout in Radial Layout Mode with Aspect Ratio 1.3
What Types of Graphs?

Tree layout is primarily designed for pure trees. It can also be used for non-trees, that is, for cyclic graphs. In this case, the algorithm computes and uses a spanning tree of the graph, ignoring all links that do not belong to the spanning tree.

Directed and undirected trees. If the links are directed, the algorithm automatically chooses the canonical root node. If the links are undirected, you can choose a root node.

Connected and disconnected graphs. If the graph is not connected, the layout algorithm treats each connected component separately. Each component has exactly one root node. In this case, a forest of trees is laid out.
Application Domains
Application domains of the Tree Layout include:

Business processing (organizational charts)

Software management/software (re-)engineering (UML diagrams, call graphs)

Database and knowledge engineering (decision trees)

The World Wide Web (Web site maps)
Features

Takes into account the size of the nodes so that no overlapping occurs.

Optionally, reshapes the links to give them an orthogonal form (alternating horizontal and vertical line segments).

Various layout modes:
free, in
levels,
radial, or
automatic tip-over.

In the free layout mode: arranges the children of each node, starting recursively from the root, so that the links flow uniformly in the same direction.

In the level layout mode: partitions the nodes into levels, and arranges the levels horizontally or vertically.

In radial layout mode: partitions the nodes into levels, and arranges the levels in circles or ellipses around the root.

In the tip-over modes: arranges the nodes in a similar way to the free layout mode, but tries to tip over children automatically to better fit the layout to the given aspect ratio.

Provides several alignment and offset options.

Allows specifying nodes that must be directly neighbored.

Takes the old position of nodes into account. Positions the nodes without changing the relative order of the nodes in the tree, so that the layout is stable on incremental changes of the graph.

Very efficient, scalable algorithm. Produces a nice layout quickly even if the number of nodes is huge.
Limitations

If “orthogonal” is not specified as the link style (see
Link Style), some links may overlap nodes, depending on the size of the nodes and the alignment and offset parameters.

The layout algorithm first determines a spanning tree of this graph. If the graph is not a pure tree, some links will not become part of the spanning tree. These links are ignored. Hence, they may cross other links or overlap nodes in the final layout.

The algorithm tries to preserve the relative order of the children of each node for incremental stability. It uses a heuristic to calculate the relative order from the old positions. The heuristic may fail if children overlap on their old positions or are neither horizontally nor vertically aligned.

Despite preserving the relative order of the children, in rare cases the layout is not perfectly stable in the radial modes. Subsequent layouts may rotate the nodes around the root, although the relative circular order of the nodes within their circular levels is still preserved.

The tip-over layout modes perform several tries with different tip-over alignment options according to various heuristics. From these, the algorithm picks the layout that best fits the given aspect ratio. This may not be the optimal layout for the aspect ratio, but it is the best layout among the performed tries. To calculate the absolutely best fitting layout is computationally infeasible (it is generally an NP-complete problem).
Version 6.3
Copyright © 2018, Rogue Wave Software, Inc. All Rights Reserved.