Hierarchical Layout
In this section, you will learn about the
Hierarchical Layout algorithm provided with the Rogue Wave Views Graph Layout package (class
IlvHierarchicalLayout from the library
ilvhierarchical).
Samples
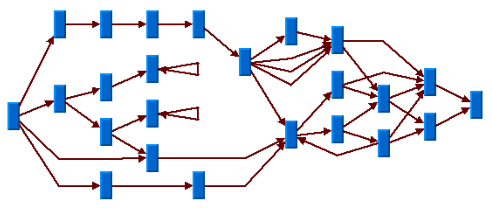
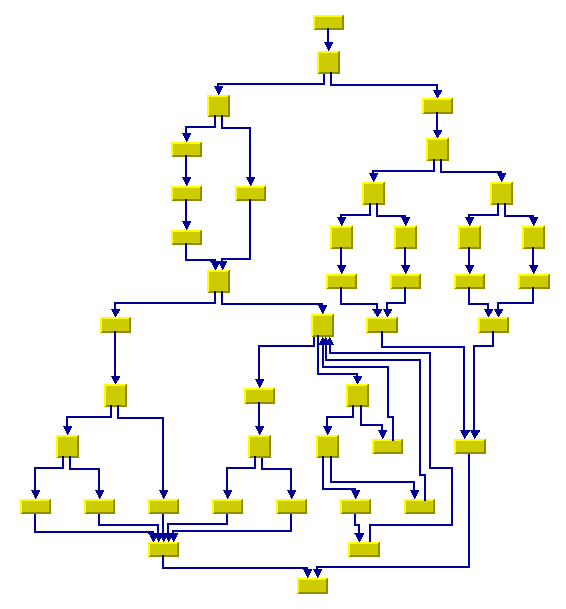
Here are some sample drawings produced with the Hierarchical Layout:
Sample Layout with Self-Loops, Multiple Links, and Cycles
Flowchart with Orthogonal Link Style
What Types of Graphs?
Any type of graph:

Preferably graphs with directed links (The algorithm takes the link direction into account.)
 Connected
Connected and
disconnected graphs
 Planar
Planar and
nonplanar graphs
Application Domains
Application domains of the Hierarchical Layout include:

Electrical engineering (logic diagrams, circuit block diagrams)

Industrial engineering (industrial process diagrams, schematic design diagrams)

Business processing (workflow diagrams, process flow diagrams, PERT charts)

Software management/software (re-)engineering (UML diagrams, flowcharts, data inspector diagrams, call graphs)

Database and knowledge engineering (database query graphs)

CASE tools (designs diagrams)
Features

Organizes nodes without overlaps in horizontal or vertical levels.

Arranges the graph such that the majority of links are short and flow uniformly in the same direction (from left to right, from top to bottom, and so on).

Reduces the number of link crossings. Most of the time, produces drawings with no crossings or only a small number of crossings.

Often produces balanced drawings that emphasize the symmetries in the graph.

Supports
self-links (that is, links with the same origin and destination node),
multiple links between the same pair of nodes, and cycles.

Efficient, scalable algorithm. Produces a nice layout relatively quickly for most sparse and medium-dense graphs, even if the number of nodes is very large.

Provides several alignment and offset options.

The computation time depends on the number of nodes, the number of levels, and the number of links that cross several levels. Most of the time, the links are placed between adjacent levels, which keeps the computation time small.
Limitations

The algorithm tries to minimize the number of
link crossings (which is generally an
NP-complete problem). It is mathematically impossible to solve this problem quickly for any graph size. Therefore, the algorithm uses a very fast heuristic that obtains a good layout, but not always with the theoretical minimum number of link crossings.

The algorithm tries to place the nodes such that all links point uniformly in the same direction. It is impossible to place cycles of links in this way. For this reason, it sometimes produces a graph where a small number of links are reversed to point in the opposite direction. The algorithm tries to minimize the number of reversed links (which, again, is an NP-complete problem). Therefore, the algorithm uses a very fast heuristic resulting in a good layout, but not always with the theoretical minimum number of reversed links.

The computation time required to obtain an appropriate drawing depends most significantly on the number of bends in the links. Since the algorithm places one bend whenever a link crosses a level, the number of bends can grow relatively quickly if the layout requires many long links that span several levels. Therefore, the layout process may become very time-consuming for dense graphs (the number of links is relatively high compared to the number of nodes) or for graphs that require a large number of node levels.
Version 6.2.1
Copyright © 2018, Rogue Wave Software, Inc. All Rights Reserved.