Determining the appropriate layout algorithm
When using the graph layout package, you need to determine which of the ready-to-use layout algorithms is appropriate for your particular needs. Some layout algorithms can handle a wide range of graphs. Others are designed for particular classes of graphs and give poor results or reject graphs that do not belong to these classes. For example, a Tree Layout algorithm is designed for
tree graphs, but not
cyclic graphs. Therefore, it is important to lay out a graph using the appropriate layout algorithm.
The following tables can help you determine which of the layout algorithms is best suited for a particular type of graph.

Across the top of the table are various classifications of different types of graphs.

The layout algorithms appear in the first column of the tables.

Table cells containing illustrations indicate when a layout algorithm is applicable for a particular type of graph.
By identifying the general characteristics of the graph you want to lay out, you can see from the tables whether a layout algorithm is suited for that particular type of graph.
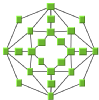
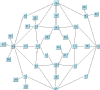
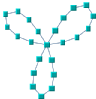
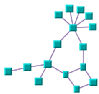
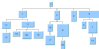
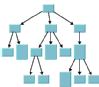
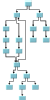
For example, if you know that the structure of the graph is a tree, you can look at the column headed Domain-independent graphs to see which layout algorithms are appropriate. The Uniform Length Edges Layout, Tree Layout, and Hierarchical Layout could all be used. Use the illustrations in the table cells to help you further narrow your choice.
You can use the
Recursive layout to control the layout of nested graphs (containing subgraphs and intergraph links). This is useful in particular if different layout styles should be applied to different subgraphs. The other layout algorithms, such as Tree Layout and Hierarchical Layout treat only flat graphs (unless otherwise noted); that is, a specific layout instance is only able to lay out the nodes and links of the attached graph, but not the nodes and links of its subgraphs. Recursive Layout allows you to specify which flat layout is used for which subgraph; it traverses the entire nested graph recursively when applying the layout. As a result, the entire nested graph is laid out.
You can use the
Multiple layout to combine several different layouts into one instance. In this case, they become
sublayouts of the Multiple Layout instance.
This is useful in particular for nested graphs when used in combination with Recursive Layout. Multiple Layout ensures that the normal layout, the routing of the intergraph links, and the layout of labels are applied in the correct order to a nested graph.
Layout algorithms and common types of graphs
Layout | Domain-independent graphs |
Trees | Cyclic Graphs | Any Graph |
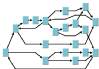
Topological Mesh Layout | | | Requires (semi)manual refinements |
Uniform Length Edges Layout | | Preferable to avoid heavily interconnected graphs (large number of links) | |
Tree Layout | | | |
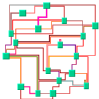
Hierarchical Layout | | | |
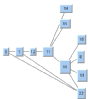
Link Layout | | | |
Grid Layout | | | The algorithm does not take into account the links between the nodes. |
Recursive Layout | | | Nested graphs. |
Multiple Layout | | | Combination of multiple different layout algorithms on the same graph (in particular for nested graphs). |
Telecom-oriented representations
Layout | Telecom-oriented representations |
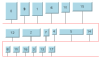
Bus Layout | For bus topologies. |
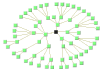
Circular Layout | For interconnected ring/star topologies. |
Copyright © 2018, Rogue Wave Software, Inc. All Rights Reserved.