

#include <rw/dsymmat.h> // DoubleSymMat #include <rw/fsymmat.h> // FloatSymMat #include <rw/csymmat.h> // DComplexSymMat DoubleSymMat A;
The classes {TYPE}SymMat represent symmetric matrices. A symmetric matrix is defined by the requirement that Aij = Aji, and so a symmetric matrix is equal to its transpose.
#include <rw/dsymmat.h>
main()
{
DoubleSymMat S(4,4,3.1); // initialize to 3.1
DoubleSymMat A = 4*S;
}
The upper triangle of the matrix is stored in column major order. The lower triangle is then calculated implicitly. The upper triangle is stored in column major order. This storage scheme was chosen so that the leading part of the matrix was always located in contiguous memory.
For example, given the following symmetric matrix:

The data is stored in the following order:
[ A11 A12 A22 A13 A23 A33 ... A1n A2n A3n ... Ann ]
The mapping between the array and storage vector is as follows:
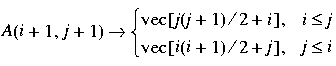
DoubleSymMat(); FloatSymMat(); DComplexSymMat();
Default constructor. Builds a matrix of size 0 x 0. This constructor is necessary to declare a matrix with no explicit constructor or to declare an array of matrices.
DoubleSymMat(const DoubleSymMat& A); FloatSymMat(const FloatSymMat& A); DComplexSymMat(const DComplexSymMat& A);
Builds a copy of their argument, A. Note that the new matrix references A's data. To construct a matrix with its own copy of the data, you can use either the copy or deepenShallowCopy member functions.
DoubleSymMat(unsigned n, unsigned n); FloatSymMat(unsigned n, unsigned n); DComplexSymMat unsigned n, unsigned n);
Defines an uninitialized matrix of size n x n. Both arguments must be equal or a runtime error occurs. This constructor is used, rather than a constructor that takes only a single argument, to avoid type conversion problems.
DoubleSymMat(unsigned n, unsigned n, double x); FloatSymMat(unsigned n, unsigned n, float x); DComplexSymMat(unsigned n, unsigned n, DComplex x);
Defines a matrix of size n x n where each element is initialized to x. Both arguments must be equal or a runtime error occurs.
DoubleSymMat(const RWMathVec<double>& vd, unsigned n,
unsigned n); FloatSymMat(const RWMathVec<float>& vd, unsigned n,
unsigned n); DComplexSymMat(const RWMathVec<DComplex>& vd, unsigned n,
unsigned n);
Constructs a size n x n matrix using the data in the passed vector. This data must be stored in the format described in the Storage Scheme section. The resultant matrix references the data in vector vd.
DComplexSymMat(const DoubleSymMat& re);
DComplexSymMat(const DoubleSymMat& re,
const DoubleSymMat& im);
Constructs a complex matrix from the real and imaginary parts supplied. If no imaginary part is supplied, it is assumed to be 0.
DoubleSymMat(const FloatSymMat&);
Constructs a copy of the argument matrix with double precision entries.
FloatSymMat FloatSymMat::apply(mathFunTy); DoubleSymMat DoubleSymMat::apply(mathFunTy); DComplexSymMat DComplexSymMat::apply(CmathFunTy); DoubleSymMat DComplexSymMat::apply(CmathFunTy2);
Returns the result of applying the passed function to every element in the matrix. A function of type mathFunTy takes and returns a double, a function of type CmathFunTy takes and returns a complex number, and a function of type CmathFunTy2 takes a complex number and returns a real number.
float& FloatSymMat::bcref(int i, int j); double& DoubleSymMat::bcref(int i, int j); DComplex& DComplexSymMat::bcref(int i, int j);
Returns a reference to the ijth element of the matrix, after doing bounds checking.
void FloatSymMat::bcset(int i, int j, float x); void DoubleSymMat::bcset(int i, int j, double x); void DComplexSymMat::bcset(int i, int j, DComplex x);
Sets the ijth element of the matrix equal to x, after doing bounds checking.
float FloatSymMat::bcval(int i, int j); double DoubleSymMat::bcval(int i, int j); DComplex DComplexSymMat::bcval(int i, int j);
Returns the value of the ijth element of the matrix, after doing bounds checking.
unsigned FloatSymMat::binaryStoreSize(); unsigned DoubleSymMat::binaryStoreSize(); unsigned DComplexSymMat::binaryStoreSize();
Returns the number of bytes that it would take to write the matrix to a file using saveOn.
unsigned FloatSymMat::cols(); unsigned DoubleSymMat::cols(); unsigned DComplexSymMat::cols();
Returns the number of columns in the matrix.
FloatSymMat FloatSymMat::copy(); DoubleSymMat DoubleSymMat::copy(); DComplexSymMat DComplexSymMat::copy();
Creates a copy of this matrix with distinct data. The stride of the data vector in the new matrix is guaranteed to be 1.
float* FloatSymMat::data(); double* DoubleSymMat::data(); DComplex* DComplexSymMat::data();
Returns a pointer to the first item of data in the vector storing the matrix's data. You can use this (with caution!) to pass the matrix's data to C or FORTRAN subroutines. Be aware that the stride of the data vector may not be 1.
RWMathVec<float> FloatSymMat::dataVec(); RWMathVec<double> DoubleSymMat::dataVec(); RWMathVec<DComplex> DComplexSymMat::dataVec();
Returns the matrix's data vector. This is where the explicitly stored entries in the matrix are kept.
FloatSymMat FloatSymMat::deepCopy(); DoubleSymMat DoubleSymMat::deepCopy(); DComplexSymMat DComplexSymMat::deepCopy();
Creates a copy of this matrix with distinct data. The stride of the data vector in the new matrix is guaranteed to be 1.
void FloatSymMat::deepenShallowCopy(); void DoubleSymMat::deepenShallowCopy(); void DComplexSymMat::deepenShallowCopy();
Ensures that the data in the matrix is not shared by any other matrix or vector. Also ensures that the stride in the data vector is equal to 1. If necessary, a new copy of the data vector is made.
FloatSymMat FloatSymMat::leadingSubmatrix(int k); DoubleSymMat DoubleSymMat::leadingSubmatrix(int k); DComplexSymMat DComplexSymMat::leadingSubmatrix(int k);
Returns the k x k upper left corner of the matrix. The submatrix and the matrix share the same data.
void FloatSymMat::printOn(ostream&); void DoubleSymMat::printOn(ostream&); void DComplexSymMat::printOn(ostream&);
Prints the matrix to an output stream in human readable format.
float& FloatSymMat::ref(int i, int j); double& DoubleSymMat::ref(int i, int j); DComplex& DComplexSymMat::ref(int i, int j);
Returns a reference to the ijth element of the matrix. Bounds checking is done if the preprocessor symbol BOUNDS_CHECK is defined when the header file is read. The member function bcref does the same thing with guaranteed bounds checking.
FloatSymMat FloatSymMat::reference(FloatSymMat&); DoubleSymMat DoubleSymMat::reference(DoubleSymMat&); DComplexSymMat DComplexSymMat::reference(DComplexSymMat&);
Makes this matrix a reference to the argument matrix. The two matrices share the same data. The matrices do not have to be the same size before calling reference. To copy a matrix into another of the same size, use the operator= member operator.
void DoubleSymMat::resize(unsigned n, unsigned n); void FloatSymMat::resize(unsigned n, unsigned n); void DComplexSymMat::resize(unsigned n, unsigned n);
Resizes the matrix. Any new entries in the matrix are set to 0. Both arguments must be the same.
void DoubleSymMat::restoreFrom(RWFile&); void FloatSymMat::restoreFrom(RWFile&); void DComplexSymMat::restoreFrom(RWFile&);
Reads in a matrix from an RWFile. The matrix must have been stored to the file using the saveOn member function.
void DoubleSymMat::restoreFrom(RWvistream&); void FloatSymMat::restoreFrom(RWvistream&); void DComplexSymMat::restoreFrom(RWvistream&);
Reads in a matrix from an RWvistream, the Rogue Wave virtual input stream class. The matrix must have been stored to the stream using the saveOn member function.
unsigned FloatSymMat::rows(); unsigned DoubleSymMat::rows(); unsigned DComplexSymMat::rows();
Returns the number of rows in the matrix.
void DoubleSymMat::saveOn(RWFile&); void FloatSymMat::saveOn(RWFile&); void DComplexSymMat::saveOn(RWFile&);
Stores a matrix to an RWFile. The matrix can be read using the restoreFrom member function.
void DoubleSymMat::saveOn(RWvostream&); void FloatSymMat::saveOn(RWvostream&); void DComplexSymMat::saveOn(RWvostream&);
Stores a matrix to an RWvostream, the Rogue Wave virtual output stream class. The matrix can be read using the restoreFrom member function.
void FloatSymMat::scanFrom(istream&); void DoubleSymMat::scanFrom(istream&); void DComplexSymMat::scanFrom(istream&);
Reads a matrix from an input stream. The format of the matrix is the same as the format output by the printTo member function. Below is a sample matrix that could be input. Note that extra white space and any text preceding the dimension specification are ignored. Only the symmetric part of the matrix is used.
3x3 [ 4 5 7
5 9 5
7 5 3 ]
void FloatSymMat::set(int i, int j, float x); void DoubleSymMat::set(int i, int j, double x); void DComplexSymMat::set(int i, int j, DComplex x);
Sets the ijth element of the matrix equal to x. Bounds checking is done if the preprocessor symbol BOUNDS_CHECK is defined when the header file is read. The member function bcset does the same thing with guaranteed bounds checking.
float FloatSymMat::val(int i, int j); double DoubleSymMat::val(int i, int j); DComplex DComplexSymMat::val(int i, int j);
Returns the value of the ijth element of the matrix. Bounds checking is done if the preprocessor symbol BOUNDS_CHECK is defined when the header file is read. The member function bcval does the same thing with guaranteed bounds checking.
FloatSymMat FloatSymMat::zero(); DoubleSymMat DoubleSymMat::zero(); DComplexSymMat DComplexSymMat::zero();
Sets every element of the matrix to 0.
double& FloatSymMat::operator()(int i, int j); double FloatSymMat::operator()(int i, int j) const; float& DoubleSymMat::operator()(int i, int j); float DoubleSymMat::operator()(int i, int j) const; DComplex& DComplexSymMat::operator()(int i, int j); DComplex DComplexSymMat::operator()(int i, int j) const;
Accesses the ijth element. If the matrix is not a const matrix, a reference type is returned, so this operator can be used for assigning or accessing an element. In this case, using this operator is equivalent to calling the ref member function. If the matrix is a const matrix, a value is returned, so this operator can be used only for accessing an element. In this case, using this operator is equivalent to calling the val member function. Bounds checking is done if the preprocessor symbol BOUNDS_CHECK is defined before including the header file.
DoubleSymMat& operator=(const DoubleSymMat& A); FloatSymMat& operator=(const FloatSymMat& A); DComplexSymMat& operator=(const DComplexSymMat& A);
Sets the matrix elements equal to the elements of A. The two matrices must be the same size. To make the matrix reference the same data as A, you can use the reference member function.
DoubleSymMat& operator=(double x); FloatSymMat& operator=(float x); DComplexSymMat& operator=(DComplex x);
Sets each element in the matrix equal to x.
DoubleSymMat& operator==(const DoubleSymMat& A); FloatSymMat& operator==(const FloatSymMat& A); DComplexSymMat& operator==(const DComplexSymMat& A); DoubleSymMat& operator!=(const DoubleSymMat& A); FloatSymMat& operator!=(const FloatSymMat& A); DComplexSymMat& operator!=(const DComplexSymMat& A);
Boolean operators. Two matrices are considered equal if they have the same size and their elements are all exactly the same. Be aware that floating point arithmetic is not exact; matrices that are theoretically equal are not always numerically equal.
DoubleSymMat& operator+=(double x); FloatSymMat& operator+=(float x); DComplexSymMat& operator+=(DComplex x); DoubleSymMat& operator-=(double x); FloatSymMat& operator-=(float x); DComplexSymMat& operator-=(DComplex x); DoubleSymMat& operator*=(double x); FloatSymMat& operator*=(float x); DComplexSymMat& operator*=(DComplex x); DoubleSymMat& operator/=(double x); FloatSymMat& operator/=(float x); DComplexSymMat& operator/=(DComplex x);
Performs the indicated operation on each element of the matrix.
DoubleSymMat& operator+=(const DoubleSymMat& A); FloatSymMat& operator+=(const FloatSymMat& A); DComplexSymMat& operator+=(const DComplexSymMat& A); DoubleSymMat& operator-=(const DoubleSymMat& A); FloatSymMat& operator-=(const FloatSymMat& A); DComplexSymMat& operator-=(const DComplexSymMat& A); DoubleSymMat& operator*=(const DoubleSymMat& A); FloatSymMat& operator*=(const FloatSymMat& A); DComplexSymMat& operator*=(const DComplexSymMat& A); DoubleSymMat& operator/=(const DoubleSymMat& A); FloatSymMat& operator/=(const FloatSymMat& A); DComplexSymMat& operator/=(const DComplexSymMat& A);
Performs element-by-element arithmetic on the data in the matrices. In particular, note that operator*= does element-by-element multiplication, not inner product style matrix multiplication. Use the product global function to do matrix-matrix inner product multiplication.
DoubleSymMat& operator++(); FloatSymMat& operator++(); DoubleSymMat& operator--(); FloatSymMat& operator--();
Increments or decrements each element in the matrix.
DoubleSymMat operator+(const DoubleSymMat&); FloatSymMat operator+(const FloatSymMat&); DComplexSymMat operator+(const DComplexSymMat&); DoubleSymMat operator-(const DoubleSymMat&); FloatSymMat operator-(const FloatSymMat&); DComplexSymMat operator-(const DComplexSymMat&);
Unary plus and minus operators. Each operator returns a copy of the matrix or its negation.
DoubleSymMat operator+(const DoubleSymMat&,
const DoubleSymMat&); FloatSymMat operator+(const FloatSymMat&,
const FloatSymMat&); DComplexSymMat operator+(const DComplexSymMat&,
const DComplexSymMat&); DoubleSymMat operator-(const DoubleSymMat&,
const DoubleSymMat&); FloatSymMat operator-(const FloatSymMat&,
const FloatSymMat&); DComplexSymMat operator-(const DComplexSymMat&,
const DComplexSymMat&); DoubleSymMat operator*(const DoubleSymMat&,
const DoubleSymMat&); FloatSymMat operator*(const FloatSymMat&,
const FloatSymMat&); DComplexSymMat operator*(const DComplexSymMat&,
const DComplexSymMat&); DoubleSymMat operator/(const DoubleSymMat&,
const DoubleSymMat&); FloatSymMat operator/(const FloatSymMat&,
const FloatSymMat&); DComplexSymMat operator/(const DComplexSymMat&,
const DComplexSymMat&);
Performs element-by-element operations on the arguments. To do inner product matrix multiplication, you can use the product global function.
DoubleSymMat operator+(double,const DoubleSymMat&); DoubleSymMat operator+(const DoubleSymMat&,double); FloatSymMat operator+(float,const FloatSymMat&); FloatSymMat operator+(const FloatSymMat&,float); DComplexSymMat operator+(DComplex,const DComplexSymMat&); DComplexSymMat operator+(const DComplexSymMat&,DComplex); DoubleSymMat operator-(double,const DoubleSymMat&); DoubleSymMat operator-(const DoubleSymMat&,double); FloatSymMat operator-(float,const FloatSymMat&); FloatSymMat operator-(const FloatSymMat&,float); DComplexSymMat operator-(DComplex,const DComplexSymMat&); DComplexSymMat operator-(const DComplexSymMat&,DComplex); DoubleSymMat operator*(double,const DoubleSymMat&); DoubleSymMat operator*(const DoubleSymMat&,double); FloatSymMat operator*(float,const FloatSymMat&); FloatSymMat operator*(const FloatSymMat&,float); DComplexSymMat operator*(DComplex,const DComplexSymMat&); DComplexSymMat operator*(const DComplexSymMat&,DComplex); DoubleSymMat operator/(double,const DoubleSymMat&); DoubleSymMat operator/(const DoubleSymMat&,double); FloatSymMat operator/(float,const FloatSymMat&); FloatSymMat operator/(const FloatSymMat&,float); DComplexSymMat operator/(DComplex,const DComplexSymMat&); DComplexSymMat operator/(const DComplexSymMat&,DComplex);
Performs element-by-element operations on the arguments.
ostream& operator<<(ostream& s, const DoubleSymMat&); ostream& operator<<(ostream& s, const FloatSymMat&); ostream& operator<<(ostream& s, const DComplexSymMat&);
Writes the matrix to the stream. This is equivalent to calling the printOn member function.
istream& operator>>(istream& s, const DoubleSymMat&); istream& operator>>(istream& s, const FloatSymMat&); istream& operator>>(istream& s, const DComplexSymMat&);
Reads the matrix from the stream. This is equivalent to calling the scanFrom member function.
DoubleSymMat abs(const DoubleSymMat&); FloatSymMat abs(const FloatSymMat&); DoubleSymMat abs(const DComplexSymMat&);
Returns a matrix whose entries are the absolute value of the argument. The absolute value of a complex number is considered to be the sum of the absolute values of its real and imaginary parts. To get the norm of a complex matrix, you can use the norm function.
DoubleSymMat arg(const DComplexSymMat& A);
Returns a matrix where each element is the argument of the corresponding element in the matrix A.
DoubleSymMat acos(const DoubleSymMat&); FloatSymMat acos(const FloatSymMat&); DoubleSymMat asin(const DoubleSymMat&); FloatSymMat asin(const FloatSymMat&); DoubleSymMat atan(const DoubleSymMat&); FloatSymMat atan(const FloatSymMat&); DoubleSymMat atan2(const DoubleSymMat&, const DoubleSymMat&); FloatSymMat atan2(const FloatSymMat&, const FloatSymMat&);
Returns a matrix where each element is formed by applying the appropriate function to each element of the argument matrix.
DoubleSymMat ceil(const DoubleSymMat&); FloatSymMat ceil(const FloatSymMat&);
Returns a matrix where each element in the matrix is the smallest integer greater than or equal to the corresponding entry in the argument matrix.
DComplexSymMat conj(const DComplexSymMat& A);
Returns a matrix where each element is the complex conjugate of the corresponding element in the matrix A.
DoubleSymMat cos(const DoubleSymMat&); FloatSymMat cos(const DoubleSymMat&); DComplexSymMat cos(const DComplexSymMat&); DoubleSymMat cosh(const DoubleSymMat&); FloatSymMat cosh(const DoubleSymMat&); DComplexSymMat cosh(const DComplexSymMat&); DoubleSymMat exp(const DoubleSymMat&); FloatSymMat exp(const DoubleSymMat&); DComplexSymMat exp(const DComplexSymMat&);
Returns a matrix where each element is formed by applying the appropriate function to each element of the argument matrix.
DoubleSymMat floor(const DoubleSymMat&); FloatSymMat floor(const FloatSymMat&);
Returns a matrix where each element in the matrix is the largest integer smaller than or equal to the corresponding entry in the argument matrix.
DoubleSymMat imag(const DComplexSymMat& A);
Returns a matrix where each element is the imaginary part of the corresponding element in the matrix A.
DoubleSymMat log(const DoubleSymMat&); FloatSymMat log(const DoubleSymMat&); DComplexSymMat log(const DComplexSymMat&); DoubleSymMat log10(const DoubleSymMat&); FloatSymMat log10(const DoubleSymMat&); DComplexSymMat log10(const DComplexSymMat&);
Returns a matrix where each element is formed by applying the appropriate function to each element of the argument matrix.
DoubleSymMat lowerToSymMat(const RWGenMat<double>& A); FloatSymMat lowerToSymMat(const RWGenMat<float>& A); DComplexSymMat lowerToSymMat(const RWGenMat<DComplex>& A);
Builds a symmetric matrix that matches the lower triangular part of A. The upper triangle of A is not referenced.
Double maxValue(const DoubleSymMat&); float maxValue(const FloatSymMat&); double minValue(const DoubleSymMat&); float minValue(const FloatSymMat&);
Returns the maximum or minimum entry in the matrix.
DoubleSymMat norm(const DComplexSymMat& A);
Returns a matrix where each element is the norm (magnitude) of the corresponding element in the matrix A.
RWMathVec<double> product(const DoubleSymMat& A, const RWMathVec<double>& x); RWMathVec<float> product(const FloatSymMat& A, const RWMathVec<float>& x); RWMathVec<DComplex> product(const DComplexSymMat& A, const RWMathVec<DComplex>& x);
Returns the inner product (matrix-vector product) of A and x.
RWMathVec<double> product(const RWMathVec<double>& x, const DoubleSymMat& A); RWMathVec<float> product(const RWMathVec<float>& x, const FloatSymMat& A); RWMathVec<DComplex> product(const RWMathVec<DComplex>& x, const DComplexSymMat& A);
Returns the inner product (matrix-vector product) of x and A. This is equal to the product of A transpose and x.
DoubleSymMat real(const DComplexSymMat& A);
Returns a matrix where each element is the real part of the corresponding element in the matrix A.
DoubleSymMat sin(const DoubleSymMat&); FloatSymMat sin(const DoubleSymMat&); DComplexSymMat sin(const DComplexSymMat&); DoubleSymMat sinh(const DoubleSymMat&); FloatSymMat sinh(const DoubleSymMat&); DComplexSymMat sinh(const DComplexSymMat&); DoubleSymMat sqrt(const DoubleSymMat&); FloatSymMat sqrt(const DoubleSymMat&); DComplexSymMat sqrt(const DComplexSymMat&);
Returns a matrix where each element is formed by applying the appropriate function to each element of the argument matrix.
DoubleSymMat tan(const DoubleSymMat&); FloatSymMat tan(const DoubleSymMat&); DComplexSymMat tan(const DComplexSymMat&); DoubleSymMat tanh(const DoubleSymMat&); FloatSymMat tanh(const DoubleSymMat&); DComplexSymMat tanh(const DComplexSymMat&);
Returns a matrix where each element is formed by applying the appropriate function to each element of the argument matrix.
FloatSymMat toFloat(const DoubleSymMat&);
Converts a matrix from double to float precision. The conversion is done using a constructor.
DoubleSymMat toSymMat(const RWGenMat<double>&); FloatSymMat toSymMat(const RWGenMat<float>&); DComplexSymMat toSymMat(const RWGenMat<DComplex>&);
Extracts the symmetric part of a square matrix. The symmetric part of a matrix A is (A+AT)/2.
DoubleSymMat transpose(const DoubleSymMat&); FloatSymMat transpose(const FloatSymMat&); DComplexSymMat transpose(const DComplexSymMat&);
Returns the transpose of the argument matrix. Since a symmetric matrix is its own transpose, this function just returns itself.
DoubleSymMat upperToSymMat(const RWGenMat<double>& A); FloatSymMat upperToSymMat(const RWGenMat<float>& A); DComplexSymMat upperToSymMat(const RWGenMat<DComplex>& A);
Builds a symmetric matrix that matches the upper triangular part of A. The lower triangle of A is not referenced.
©Copyright 1999, Rogue Wave Software, Inc.
Send mail to report errors or comment on the documentation.