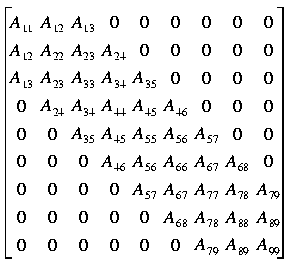

#include <rw/dsbndmat.h> // DoubleSymBandMat #include <rw/fsbndmat.h> // FloatSymBandMat #include <rw/csbndmat.h> // DComplexSymBandMat DoubleSymBandMat d;
The classes {TYPE}SymBandMat encapsulate symmetric band matrices. A symmetric banded matrix is symmetric, and nonzero only near the diagonal. Specifically, if h is the half bandwidth, then any entries for which i-j>h or j-i>h are defined to be 0; in addition, an entry Aij = Aji.
#include <rw/fsbndmat.h>
main()
{
FloatSymBandMat SB(4,4,1);
SB.diagonal(-1) = -1;
SB.diagonal( ) = 0;
SB.diagonal( 1) = 1;
}
As an example of the storage scheme, consider the following 9 x 9 matrix with a half bandwidth of two:
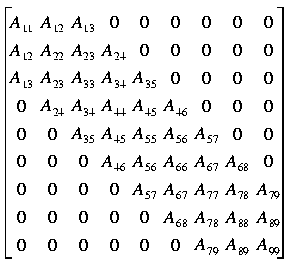
The upper triangle is stored column by column. For convenience, there are some unused locations left in the vector of data. These are indicated as XXX in the following illustration of the storage vector:
[ XXX XXX A11 XXX A12 A22 A13 A23 A33 A24 A34 A44 A35 A45 A55
A46 A56 A66 A57 A67 A77 A68 A78 A88 A79 A89 A99 ]
The mapping between the array and storage vector is as follows:
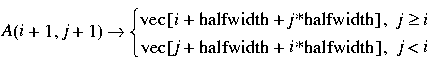
DoubleSymBandMat(); FloatSymBandMat(); DComplexSymBandMat();
Default constructor. Builds a matrix of size 0 x 0. This constructor is necessary to declare a matrix with no explicit constructor or to declare an array of matrices.
DoubleSymBandMat(const DoubleSymBandMat& A); FloatSymBandMat(const FloatSymBandMat& A); DComplexSymBandMat(const DComplexSymBandMat& A);
Build a copy of its argument, A. Note that the new matrix references A's data. To construct a matrix with its own copy of the data, you can use either the copy or deepenShallowCopy member functions.
DoubleSymBandMat(unsigned n, unsigned n, unsigned hb); FloatSymBandMat(unsigned n, unsigned n, unsigned hb); DComplexSymBandMat(unsigned n, unsigned n, unsigned hb);
Defines an uninitialized matrix of size n x n with half bandwidth hb.
DoubleSymBandMat(const RWMathVec<double>& vd,
unsigned n, unsigned n, unsigned hb);
FloatSymBandMat(const RWMathVec<float>& vd, unsigned n,
unsigned n, unsigned hb);
DComplexSymBandMat(const RWMathVec<DComplex>& vd, unsigned n,
unsigned n, unsigned hb);
Constructs an n x n matrix with half bandwidth hb using the data in the passed vector. This data must be stored in the format described in the Storage Scheme section. The resultant matrix references the data in
vector vd.
DComplexSymBandMat(const DoubleSymBandMat& re);
DComplexSymBandMat(const DoubleSymBandMat& re,
const DoubleSymBandMat& im);
Constructs a complex matrix from the real and imaginary parts supplied. If no imaginary part is supplied, it is assumed to be 0.
DoubleSymBandMat(const FloatSymBandMat&);
Constructs a copy of the argument matrix with double precision entries.
unsigned FloatSymBandMat::bandwidth(); unsigned DoubleSymBandMat::bandwidth(); unsigned DComplexSymBandMat::bandwidth();
Returns the bandwidth of the matrix. The bandwidth is twice the half bandwidth plus 1 for the main diagonal.
RWMathVec<float> FloatSymBandMat::bcdiagonal(int j=0); RWMathVec<double> DoubleSymBandMat::bcdiagonal(int j=0); RWMathVec<DComplex> DComplexSymBandMat::bcdiagonal(int j=0);
Returns a reference to the jth diagonal of the matrix, after doing bounds checking. The main diagonal is indexed by 0, diagonals in the upper triangle are indexed with positive integers, diagonals in the lower triangle are indexed with negative integers.
ROFloatRef FloatSymBandMat::bcref(int i, int j); RODoubleRef DoubleSymBandMat::bcref(int i, int j); RODComplexRef DComplexSymBandMat::bcref(int i, int j);
Returns a reference to the ijth element of the matrix, after doing bounds checking.
void FloatSymBandMat::bcset(int i, int j, float x); void DoubleSymBandMat::bcset(int i, int j, double x); void DComplexSymBandMat::bcset(int i, int j, DComplex);
Sets the ijth element of the matrix equal to x, after doing bounds checking.
float FloatSymBandMat::bcval(int i, int j); double DoubleSymBandMat::bcval(int i, int j); DComplex DComplexSymBandMat::bcval(int i, int j);
Returns the value of the ijth element of the matrix, after doing bounds checking.
unsigned FloatSymBandMat::binaryStoreSize(); unsigned DoubleSymBandMat::binaryStoreSize(); unsigned DComplexSymBandMat::binaryStoreSize();
Returns the number of bytes that it would take to write the matrix to a file using saveOn.
unsigned FloatSymBandMat::cols(); unsigned DoubleSymBandMat::cols(); unsigned DComplexSymBandMat::cols();
Returns the number of columns in the matrix.
FloatSymBandMat FloatSymBandMat::copy(); DoubleSymBandMat DoubleSymBandMat::copy(); DComplexSymBandMat DComplexSymBandMat::copy();
Creates a copy of this matrix with distinct data. The stride of the data vector in the new matrix is guaranteed to be 1.
float* FloatSymBandMat::data(); double* DoubleSymBandMat::data(); DComplex* DComplexSymBandMat::data();
Returns a pointer to the first item of data in the vector storing the matrix's data. You can use this (with caution!) to pass the matrix's data to C or FORTRAN subroutines. Be aware that the stride of the data vector may not be 1.
RWMathVec<float> FloatSymBandMat::dataVec(); RWMathVec<double> DoubleSymBandMat::dataVec(); RWMathVec<DComplex> DComplexSymBandMat::dataVec();
Returns the matrix's data vector. This is where the explicitly stored entries in the matrix are kept.
FloatSymBandMat FloatSymBandMat::deepCopy(); DoubleSymBandMat DoubleSymBandMat::deepCopy(); DComplexSymBandMat DComplexSymBandMat::deepCopy();
Creates a copy of this matrix with distinct data. The stride of the data vector in the new matrix is guaranteed to be 1.
void FloatSymBandMat::deepenShallowCopy(); void DoubleSymBandMat::deepenShallowCopy(); void DComplexSymBandMat::deepenShallowCopy();
Ensures that the data in the matrix is not shared by any other matrix or vector. Also ensure that the stride in the data vector is equal to 1. If necessary, a new copy of the data vector is made.
RWMathVec<float> FloatSymBandMat::diagonal(int j=0); RWMathVec<double> DoubleSymBandMat::diagonal(int j=0); RWMathVec<DComplex> DComplexSymBandMat::diagonal(int j=0);
Returns a reference to the jth diagonal of the matrix. The main diagonal is indexed by 0, diagonals in the upper triangle are indexed with positive integers, and diagonals in the lower triangle are indexed with negative integers. Bounds checking is done if the preprocessor symbol BOUNDS_CHECK is defined when the header file is read. The member function bcdiagonal does the same thing with guaranteed bounds checking.
unsigned FloatSymBandMat::halfBandwidth(); unsigned DoubleSymBandMat::halfBandwidth(); unsigned DComplexSymBandMat::halfBandwidth();
Returns the half bandwidth of the matrix.
FloatSymBandMat FloatSymBandMat::leadingSubmatrix(int k); DoubleSymBandMat DoubleSymBandMat::leadingSubmatrix(int k); DComplexSymBandMat DComplexSymBandMat::leadingSubmatrix(int k);
Returns the k x k upper left corner of the matrix. The submatrix and the matrix share the same data.
unsigned FloatSymBandMat::lowerBandwidth(); unsigned DoubleSymBandMat::lowerBandwidth(); unsigned DComplexSymBandMat::lowerBandwidth();
Returns the lower bandwidth of the matrix.
void FloatSymBandMat::printOn(ostream&); void DoubleSymBandMat::printOn(ostream&); void DComplexSymBandMat::printOn(ostream&);
Prints the matrix to an output stream in human readable format.
ROFloatRef FloatSymBandMat::ref(int i, int j); RODoubleRef DoubleSymBandMat::ref(int i, int j); RODComplexRef DComplexSymBandMat::ref(int i, int j);
Returns a reference to the ijth element of the matrix. Bounds checking is done if the preprocessor symbol BOUNDS_CHECK is defined when the header file is read. The member function bcref does the same thing with guaranteed bounds checking.
FloatSymBandMat FloatSymBandMat::reference(FloatSymBandMat&); DoubleSymBandMat DoubleSymBandMat::reference(DoubleSymBandMat&); DComplexSymBandMat DComplexSymBandMat::reference(DComplexSymBandMat&);
Makes this matrix a reference to the argument matrix. The two matrices share the same data. The matrices do not have to be the same size before calling reference. To copy a matrix into another of the same size, use the operator= member operator.
void DoubleSymBandMat::resize(unsigned n, unsigned n); void FloatSymBandMat::resize(unsigned n, unsigned n); void DComplexSymBandMat::resize(unsigned n,unsigned n); void DoubleSymBandMat::resize(unsigned n, unsigned n, unsigned hb); void FloatSymBandMat::resize(unsigned n, unsigned n, unsigned hb); void DComplexSymBandMat::resize(unsigned n,unsigned n, unsigned hb);
Resizes the matrix or changes both its size and half bandwidth. Any new entries in the matrix are set to 0. Both arguments must be the same.
void DoubleSymBandMat::restoreFrom(RWFile&); void FloatSymBandMat::restoreFrom(RWFile&); void DComplexSymBandMat::restoreFrom(RWFile&);
Reads in a matrix from an RWFile. The matrix must have been stored to the file using the saveOn member function.
void DoubleSymBandMat::restoreFrom(RWvistream&); void FloatSymBandMat::restoreFrom(RWvistream&); void DComplexSymBandMat::restoreFrom(RWvistream&);
Reads in a matrix from an RWvistream, the Rogue Wave virtual input stream class. The matrix must have been stored to the stream using the saveOn member function.
unsigned FloatSymBandMat::rows(); unsigned DoubleSymBandMat::rows(); unsigned DComplexSymBandMat::rows();
Returns the number of rows in the matrix.
void DoubleSymBandMat::saveOn(RWFile&); void FloatSymBandMat::saveOn(RWFile&); void DComplexSymBandMat::saveOn(RWFile&);
Stores a matrix to an RWFile. The matrix can be read using the restoreFrom member function.
void DoubleSymBandMat::saveOn(RWvostream&); void FloatSymBandMat::saveOn(RWvostream&); void DComplexSymBandMat::saveOn(RWvostream&);
Stores a matrix to an RWvostream, the Rogue Wave virtual output stream class. The matrix can be read using the restoreFrom member function.
void FloatSymBandMat::scanFrom(istream&); void DoubleSymBandMat::scanFrom(istream&); void DComplexSymBandMat::scanFrom(istream&);
Reads a matrix from an input stream. The format of the matrix is the same as the format output by the printTo member function: first the half bandwidth, followed by the matrix itself. Below is a sample matrix showing the format. Note that extra white space and text preceding the bandwidth specification are ignored. Only the symmetric part of the relevant band of the matrix is used.
1 5x5 [ 3 7 0 0 0 7 2 2 0 0 0 2 8 9 0 0 0 9 8 7 0 0 0 7 8 ]
void FloatSymBandMat::set(int i, int j, float x); void DoubleSymBandMat::set(int i, int j, double x); void DComplexSymBandMat::set(int i, int j, DComplex x);
Sets the ijth element of the matrix equal to x. Bounds checking is done if the preprocessor symbol BOUNDS_CHECK is defined when the header file is read. The member function bcset does the same thing with guaranteed bounds checking.
unsigned FloatSymBandMat::upperBandwidth(); unsigned DoubleSymBandMat::upperBandwidth(); unsigned DComplexSymBandMat::upperBandwidth();
Returns the upper bandwidth of the matrix.
float FloatSymBandMat::val(int i, int j); double DoubleSymBandMat::val(int i, int j); DComplex DComplexSymBandMat::val(int i, int j);
Returns the value of the ijth element of the matrix. Bounds checking is done if the preprocessor symbol BOUNDS_CHECK is defined when the header file is read. The member function bcval does the same thing with guaranteed bounds checking.
FloatSymBandMat FloatSymBandMat::zero(); DoubleSymBandMat DoubleSymBandMat::zero(); DComplexSymBandMat DComplexSymBandMat::zero();
Sets every element of the matrix to 0.
RODoubleRef FloatSymBandMat::operator()(int i, int j); double FloatSymBandMat::operator()(int i, int j) const; ROFloatRef DoubleSymBandMat::operator()(int i, int j); float DoubleSymBandMat::operator()(int i, int j) const; RODComplexRef DComplexSymBandMat::operator()(int i, int j); DComplex DComplexSymBandMat::operator()(int i,int j) const;
Accesses the ijth element. If the matrix is not a const matrix, a reference type is returned, so this operator can be used for assigning or accessing an element. In this case, using this operator is equivalent to calling the ref member function. If the matrix is a const matrix, a value is returned so this operator can be used only for accessing an element. In this case, using this operator is equivalent to calling the val member function. Bounds checking is done if the preprocessor symbol BOUNDS_CHECK is defined before including the header file.
DoubleSymBandMat& operator=(const DoubleSymBandMat& A); FloatSymBandMat& operator=(const FloatSymBandMat& A); DComplexSymBandMat& operator=(const DComplexSymBandMat& A);
Sets the matrix elements equal to the elements of A. The two matrices must be the same size. To make the matrix reference the same data as A, use the reference member function.
DoubleSymBandMat& operator==(const DoubleSymBandMat& A); FloatSymBandMat& operator==(const FloatSymBandMat& A); DComplexSymBandMat& operator==(const DComplexSymBandMat& A); DoubleSymBandMat& operator!=(const DoubleSymBandMat& A); FloatSymBandMat& operator!=(const FloatSymBandMat& A); DComplexSymBandMat& operator!=(const DComplexSymBandMat& A);
Boolean operators. Two matrices are considered equal if they have the same size and their elements are all exactly the same. Be aware that floating point arithmetic is not exact; matrices that are theoretically equal are not always numerically equal.
DoubleSymBandMat& operator*=(double x); FloatSymBandMat& operator*=(float x); DComplexSymBandMat& operator*=(DComplex x); DoubleSymBandMat& operator/=(double x); FloatSymBandMat& operator/=(float x); DComplexSymBandMat& operator/=(DComplex x);
Performs the indicated operation on each element of the matrix.
DoubleSymBandMat& operator+=(const DoubleSymBandMat& A); FloatSymBandMat& operator+=(const FloatSymBandMat& A); DComplexSymBandMat& operator+=(const DComplexSymBandMat& A); DoubleSymBandMat& operator-=(const DoubleSymBandMat& A); FloatSymBandMat& operator-=(const FloatSymBandMat& A); DComplexSymBandMat& operator-=(const DComplexSymBandMat& A); DoubleSymBandMat& operator*=(const DoubleSymBandMat& A); FloatSymBandMat& operator*=(const FloatSymBandMat& A); DComplexSymBandMat& operator*=(const DComplexSymBandMat& A); DoubleSymBandMat& operator/=(const DoubleSymBandMat& A); FloatSymBandMat& operator/=(const FloatSymBandMat& A); DComplexSymBandMat& operator/=(const DComplexSymBandMat& A);
Performs element-by-element arithmetic on the data in the matrices. In particular, note that operator*= does element-by-element multiplication, not inner product style matrix multiplication. You can use the product global function to do matrix-matrix inner product multiplication.
DoubleSymBandMat operator+(const DoubleSymBandMat&); FloatSymBandMat operator+(const FloatSymBandMat&); DComplexSymBandMat operator+(const DComplexSymBandMat&); DoubleSymBandMat operator-(const DoubleSymBandMat&); FloatSymBandMat operator-(const FloatSymBandMat&); DComplexSymBandMat operator-(const DComplexSymBandMat&);
Unary plus and minus operators. Each operator returns a copy of the matrix or its negation.
DoubleSymBandMat operator+(const DoubleSymBandMat&,
const DoubleSymBandMat&); FloatSymBandMat operator+(const FloatSymBandMat&,
const FloatSymBandMat&); DComplexSymBandMat operator+(const DComplexSymBandMat&,
const DComplexSymBandMat&); DoubleSymBandMat operator-(const DoubleSymBandMat&,
const DoubleSymBandMat&); FloatSymBandMat operator-(const FloatSymBandMat&,
const FloatSymBandMat&); DComplexSymBandMat operator-(const DComplexSymBandMat&,
const DComplexSymBandMat&); DoubleSymBandMat operator*(const DoubleSymBandMat&,
const DoubleSymBandMat&); FloatSymBandMat operator*(const FloatSymBandMat&,
const FloatSymBandMat&); DComplexSymBandMat operator*(const DComplexSymBandMat&,
const DComplexSymBandMat&); DoubleSymBandMat operator/(const DoubleSymBandMat&,
const DoubleSymBandMat&); FloatSymBandMat operator/(const FloatSymBandMat&,
const FloatSymBandMat&); DComplexSymBandMat operator/(const DComplexSymBandMat&,
const DComplexSymBandMat&);
Performs element-by-element operations on the arguments. To do inner product matrix multiplication, you can use the product global function.
DoubleSymBandMat operator*(double,const DoubleSymBandMat&); DoubleSymBandMat operator*(const DoubleSymBandMat&,double); FloatSymBandMat operator*(float,const FloatSymBandMat&); FloatSymBandMat operator*(const FloatSymBandMat&,float); DComplexSymBandMat operator*(DComplex,
const DComplexSymBandMat&); DComplexSymBandMat operator*(const DComplexSymBandMat&,
DComplex); DoubleSymBandMat operator/(const DoubleSymBandMat&, double); FloatSymBandMat operator/(const FloatSymBandMat&,float); DComplexSymBandMat operator/(const DComplexSymBandMat&,
DComplex);
Performs element-by-element operations on the arguments.
ostream& operator<<(ostream& s, const DoubleSymBandMat&); ostream& operator<<(ostream& s, const FloatSymBandMat&); ostream& operator<<(ostream& s, const DComplexSymBandMat&);
Writes the matrix to the stream. This is equivalent to calling the printOn member function.
istream& operator>>(istream& s, const DoubleSymBandMat&); istream& operator>>(istream& s, const FloatSymBandMat&); istream& operator>>(istream& s, const DComplexSymBandMat&);
Reads the matrix from the stream. This is equivalent to calling the scanFrom member function.
DoubleSymBandMat abs(const DoubleSymBandMat&); FloatSymBandMat abs(const FloatSymBandMat&); DoubleSymBandMat abs(const DComplexSymBandMat&);
Returns a matrix whose entries are the absolute value of the argument. The absolute value of a complex number is considered to be the sum of the absolute values of its real and imaginary parts. To get the norm of a complex matrix, you can use the norm function.
DoubleSymBandMat arg(const DComplexSymBandMat& A);
Returns a matrix where each element is the argument of the corresponding element in the matrix A.
DComplexSymBandMat conj(const DComplexSymBandMat& A);
Returns a matrix where each element is the complex conjugate of the corresponding element in the matrix A.
DoubleSymBandMat imag(const DComplexSymBandMat& A);
Returns a matrix where each element is the imaginary part of the corresponding element in the matrix A.
double maxValue(const DoubleSymBandMat&); float maxValue(const FloatSymBandMat&); double minValue(const DoubleSymBandMat&); float minValue(const FloatSymBandMat&);
Returns the maximum or minimum entry in the matrix.
DoubleSymBandMat norm(const DComplexSymBandMat& A);
Returns a matrix where each element is the norm (magnitude) of the corresponding element in the matrix A.
RWMathVec<double> product(const DoubleSymBandMat& A, const RWMathVec<double>& x); RWMathVec<float> product(const FloatSymBandMat& A, const RWMathVec<float>& x); RWMathVec<DComplex> product(const DComplexSymBandMat& A, const RWMathVec<DComplex>& x);
Returns the inner product (matrix-vector product) of A and x.
RWMathVec<double> product(const RWMathVec<double>& x, const DoubleSymBandMat& A); RWMathVec<float> product(const RWMathVec<float>& x, const FloatSymBandMat& A); RWMathVec<DComplex> product(const RWMathVec<DComplex>& x,const DComplexSymBandMat& A);
Returns the inner product (matrix-vector product) of x and A. This is equal to the product of A transpose and x.
DoubleSymBandMat real(const DComplexSymBandMat& A);
Returns a matrix where each element is the real part of the corresponding element in the matrix A.
FloatSymBandMat toFloat(const DoubleSymBandMat&);
Converts a matrix from double to float precision. The conversion is done using a constructor.
DoubleSymBandMat toSymBandMat(const RWGenMat<double>&); FloatSymBandMat toSymBandMat(const RWGenMat<float>&); DComplexSymBandMat toSymBandMat(const RWGenMat<DComplex>&);
Extracts the symmetric part of a band of entries from a square matrix. The main diagonal is extracted, along with h subdiagonals and superdiagonals. If B is this band, the symmetric part of the band is (B+BT)/2.
DoubleSymBandMat transpose(const DoubleSymBandMat&); FloatSymBandMat transpose(const FloatSymBandMat&); DComplexSymBandMat transpose(const DComplexSymBandMat&);
Returns the transpose of the argument matrix.
©Copyright 1999, Rogue Wave Software, Inc.
Send mail to report errors or comment on the documentation.