This section introduces some of the mathematical concepts used with PV‑WAVE.

A fast Fourier transform (FFT) is simply a discrete Fourier transform that is computed efficiently. Basically, the straightforward method for computing the Fourier transform takes approximately n2 operations, where n is the number of points in the transform, while the FFT (which computes the same values) takes approximately nlogn operations. The algorithms in this chapter are modeled after the Cooley-Tukey (1965) algorithm. Hence, these functions are most efficient for integers that are highly composite, that is, integers that are a product of the small primes 2, 3, and 5.

For the function FFTCOMP, there is a corresponding initialization function. Use this function only when repeatedly transforming one-dimensional sequences of the same data type and length. In this situation, the initialization function computes the initial setup once; subsequently, the user calls the main function with the appropriate keyword. This may result in substantial computational savings. For more information on the use of these functions, consult the documentation under the appropriate function name. In addition to the one-dimensional transformation described above, the function FFTCOMP also can be used to compute a complex two-dimensional FFT and its inverse.

There is a close connection between the discrete Fourier transform and the continuous Fourier transform. The continuous Fourier transform is defined by Brigham (1974) as follows:

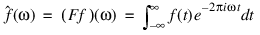
Begin by making the following approximation:

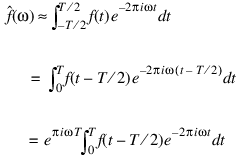
If the last integral approximated using the rectangle rule with spacing h = T/n, the result is given below:

Finally, setting ω = j / T for j = 0, ..., n – 1 yields:

where the vector fh = (f (–T / 2), ..., f ((n – 1) h – T / 2)). Thus, after scaling the components by (–1) jh, the discrete Fourier transform as computed in FFTCOMP (with input f h) is related to an approximation of the continuous Fourier transform by the above formula.

If the function f is expressed as a function, then the continuous Fourier transform:

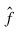
can be approximated using the PV‑WAVE IMSL Mathematics function INTFCN to compute a Fourier transform as described in INTFCN Function on page 192 in Chapter Chapter 5: Quadrature.