IIRFILT Function
Applies an infinite impulse response (IIR) filter to a data sequence.
Usage
result = IIRFILT(h, x)
Input Parameters
h—A digital filter structure containing the filter coefficients.
x—A one-dimensional array containing the data to be filtered.
Returned Value
result—A one-dimensional array containing the filtered data. The returned array is the same dimension as the input array x.
Keywords
Forward_back—If present and nonzero, use the forward-backward method.
init—Vector of initial conditions from the FILTIC Function .
Discussion
IIRFILT realizes the digital filter:
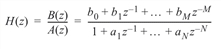
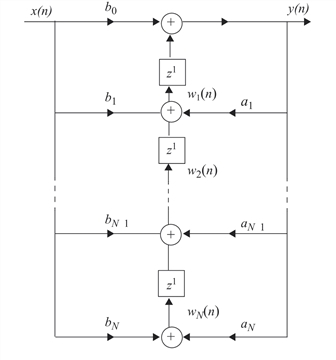
using the transposed direct form II filter structure shown in Signal Flow Graph for IIR Filter Realization.
|
|
The difference equations associated with this filter structure are given by:
y(n) = w1(n – 1) + b0x(n)
wk(n) = wk+1(n – 1) – aky(n) + bkx(n) , k = 1, 2, ..., max{M, N}
wN(n) = bNx(n) – aNy(n)
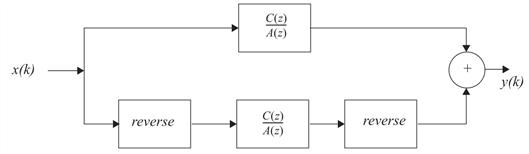
When the keyword Forward_back is specified, this function filters the data sequence in both the forward and backward directions. Forward-backward filtering is equivalent to applying the filter:

The algorithm used to accomplish the forward-backward filter operation first solves the equation:
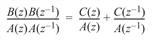
for C(z) using the Jury algorithm discussed in Demeure and Mullis (1990). The signal is then filtered according to the signal flow diagram shown in Signal Flow Diagram for Forward-Backward Filtering.
|
|
The “reverse” operation shown in the figure takes a sequence:
x(k), k = 0, 1, ..., L
and replaces it with the sequence:
x(L – k), k = 0, 1, ..., L
Forward-backward filtering is typically used to obtain zero-phase response from an IIR filter.
|
Note: |
Each of these methods assumes that the constant term in the denominator polynomial of the transfer function is unity. To satisfy that assumption, both the numerator and denominator polynomials are scaled by a0. |
Example
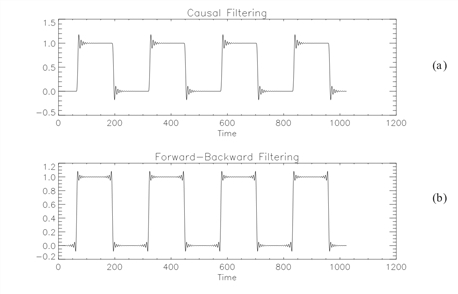
In this example, IIRFILT is used to perform causal and anti-causal filtering. The results are shown in IIRFILT Function example, where (a) is causal and (b) is the anti-causal filtering of a square wave accomplished using the IIRFILT function.
!P.multi = [0, 1, 2]
; Generate a square wave.
x = ((INDGEN(1024)+64) MOD 256) GT 128
; Design an elliptic lowpass filter.
h = IIRDESIGN(5, 0.25, 0.01, 0.01, /Ellip)
; Causal filtering of the square wave.
PLOT, IIRFILT(h, x), Title = 'Causal Filtering', XTitle = 'Time'
; Anti-causal (forward-backward) filtering of square wave.
PLOT, IIRFILT(h, x, /Forward_back), $
Title = 'Forward-Backward Filtering', XTitle = 'Time'
|
|
See Also
For Additional Information
Proakis and Manolakis, 1992.
Demeure and Mullis, 1990.