POLYCYLN Function
Generates polygons to describe the surface of a rotated curve.
Usage
p = POLYCYLN(a, d, c, n)
Input Parameters
a — A (3,2) array defining orientation for the axis of rotation.
d — The number of degrees of right-hand rotation about the axis.
c — A (m,3) array defining the curve.
n — A number of vertices for the angular dimension of the surface.
Returned Value
p — A 2-element list where p(0) is the (m*n, 3) array of vertices for the surface obtained from the n rotations of the m curve vertices. p(1) is a 1D array defining the polygons: p(1) = [4, i11, i12, i13, i14, ..., 4, imn1, imn2, imn3, imn4] where the i* are indices into the first dimension of p(0).
Keywords
None.
Discussion
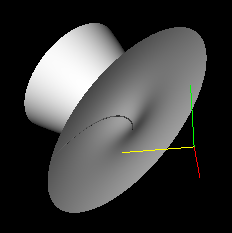
The POLYCYLN function generates polygons that describe a surface of revolution. The axis of revolution is arbitrary as is the number of degrees of rotation. Also completely arbitrary, is the curve to be rotated about the axis. The polygonal output can be imported into VtkPolyShade.
Example
t = INTERPOL([-1,1],101)
c = [[t], [t*t], [t*t*t]] + 1
a = [[1, 1, 1], [1, 2, 2]]
p = POLYCYLN(a, 360, c, 91)
VTKWINDOW, /NoRender
VTKPOLYSHADE, TRANSPOSE(p(0)), p(1), /NoAxes
VTKAXES
VTKPLOTS, TRANSPOSE(c), Color=128
VTKPLOTS, a, Color=128
VTKRENDERWINDOW
|
|