CHNNDSOL Function

Solves a real symmetric nonnegative definite system of linear equations Ax = b. Computes the solution to Ax = b given the Cholesky factor.

Usage

result = CHNNDSOL(b[, a])

Input Parameters

b—Matrix containing the right-hand side.

a—(Optional) Two-dimensional matrix containing the coefficient matrix. Element A(i, j) contains the j^th coefficient of the i^th equation.

Returned Value

result—A solution x of the linear system Ax = b.

Input Keywords

Double—If present and nonzero, double precision is used.

Factor—The LL^T factorization of A. The lower-triangular part of this matrix contains L, and the upper-triangular part contains L^T.

Tolerance—Tolerance used in determining linear dependence. Default: Tolerance = 100e, where e is machine precision.

Output Keywords

Inverse—Specifies a named variable into which the inverse of the matrix A is stored.

Discussion

Function CHNNDSOL solves a system of linear algebraic equations having a symmetric nonnegative definite (positive semidefinite) coefficient matrix. It first computes a Cholesky (LL^H or R^HR) factorization of the coefficient matrix A.

The factorization algorithm is based on the work of Healy (1968) and proceeds sequentially by columns. The i^th column is declared to be linearly dependent on the first i – 1 columns if:

 

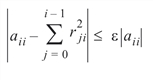
where e (specified by Tolerance) may be set by the user. When a linear dependence is declared, all elements in the i^th row of R (column of L) are set to zero.

Modifications due to Farebrother and Berry (1974) and Barrett and Healy (1978) for checking for matrices that are not nonnegative definite also are incorporated. The CHNNDSOL function declares A to be not nonnegative definite and issues an error message if either of the following conditions is satisfied:

1.

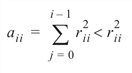
2.  

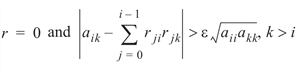
Healy’s (1968) algorithm and function CHNNDSOL permit the matrices A and R to occupy the same storage. Barrett and Healy (1978), in their remark, neglect this fact. The CHNNDSOL function uses:

 

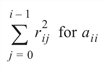
in condition 2 above to remedy this problem.

If an inverse of the matrix A is required and the matrix is not (numerically) positive definite, then the resulting inverse is a symmetric g₂ inverse of A. For a matrix G to be a g₂ inverse of a matrix A, G must satisfy conditions 1 and 2 for the Moore-Penrose inverse but generally fail conditions 3 and 4. The four conditions for G to be a Moore-Penrose inverse of A are as follows:

3. AGA = A

4. GAG = G

5. AG is symmetric

6. GA is symmetric

The solution of the linear system Ax = b is computed by solving the factored version of the linear system R^TRx = b as two successive triangular linear systems. In solving the triangular linear systems, if the elements of a row of R are all zero, the corresponding element of the solution vector is set to zero. For a detailed description of the algorithm, see Section 2 in Sallas and Lionti (1988). This routine is useful to solve normal equations in a linear least-squares problem.

Example

A solution to a system of four linear equations is obtained. Maindonald (1984, pp. 83–86, 104–105) discusses the computations for the factorization and solution to this problem.

; Define the coefficient matrix.

RM, a, 4, 4

row 0: 36 12 30  6

row 1: 12 20  2 10

row 2: 30  2 29  1

row 3:  6 10  1 14

; Define the right-hand side.

RM, b, 4, 1

row 0: 18

row 1: 22

row 2:  7

row 3: 20

; Define the right-hand side.

x = CHNNDSOL(b, a)

; Output the results.

PM, x

; PV-WAVE prints the following:

; 0.166667

; 0.500000

; 0.00000

; 1.00000

Warning Errors

MATH_INCONSISTENT_EQUATIONS_2—Linear system of equations is inconsistent.

MATH_NOT_NONNEG_DEFINITE—Matrix A is not nonnegative definite.