Combining Array Subscripts with Others
Array subscripts may be combined with:
Subscript rangesSimple scalar subscriptsOther array subscriptsWhen it encounters a multidimensional subscript that contains one or more subscript arrays, PV-WAVE builds an array of subscripts by processing each subscript, from left to right. The resulting array of subscripts is then applied to the variable that is to be subscripted.
As with other subscript operations, trailing degenerate dimensions (those with a size of 1) are eliminated.
Combining Array Subscripts with Scalar or Range Subscripts
When combining an n-element subscript array with an m-element subscript range, the resulting subarray is of dimension n by m.
For example, the expression A([1,3],5) yields the vector [A1,5, A3,5], and the expression A([1, 3, 5], 7 : 9) yields a 3-by-3 array composed of the elements:
Each element of the 3-element subscript array (1, 3, 5) is combined with each element of the 3-element range (7, 8, 9).
Examples
The common process of zeroing the edge elements of a two-dimensional n-by-m array is:
A(*, [0, M - 1]) = 0
A([0, N - 1], *) = 0
For another example of combining array and range subscripts, consider:
A = DBLARR( 5, 10, 5, 10, 5 )
B = [-1, 0, 5, 3.9]
INFO, A(B, *, 2:*, 1:3, 0)
; <Expression> DOUBLE = Array(4, 10, 3, 3)
Combining with Other Subscript Arrays
If all subscripts are arrays, then all these arrays must have the same number of elements; in this case, each element of the first subscript array is combined with the corresponding elements of the other subscript arrays.
For example:
a=FINDGEN(6,6) & PM, a([0,2,4], [1,3,5])
; PV-WAVE prints the following:
; 6.00000 (= A0,1); 20.0000 (= A2,3); 34.0000 (= A4,5)Or, if A is a 3D array, then:
A([0,2], [1,3], [0,2]) = 10
assigns the value 10 to the elements A010, A232.
If multiple array subscripts are mixed with scalars or ranges, then the resulting subscript array is the Cartesian product of all of the subscripts. For example, if A is a 3D array, then the expression A([0,2,3],[1,3],0) yields the 2D array:
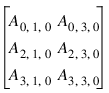
Also, note that since extra “0 dimensions” are allowed, a 2D array A can be subscripted with the Cartesian product of two subscript arrays. For example, the expression A([0,2,3],[1,3],0) yields the 2D array:
