BESELY Function
Calculates the Bessel Y function for the input parameter.
Usage
result = BESELY(x[, n])
Input Parameters
x—The expression that is evaluated. This expression must be > 0.
n—(optional) An integer. (Default: 0)
Returned Value
result—The Bessel Y function for x, having the same dimensions as x.
Keywords
None.
Discussion
The Bessel Y function is one of a mathematical series that arise in solving differential equations for systems with cylindrical symmetry. The Bessel series can be useful in communications and signal processing, since they give the relative amplitude of the spectral components of a frequency-modulated carrier wave.
Bessel Y is a Bessel function of the second order. Unlike the Bessel J function, it has no finite limit as x approaches zero. BESELY is a numerical approximation to the solution of the differential equation for a real x:
x2 * y'' + x * y' + (x2 – n2) * y = 0 n ≥ 0
The BESELY function is a solution of the second kind of Bessel functions of order n. The general solution of the above differential equation using the BESELJ function is as follows:
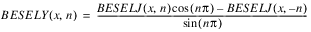
when n ≠ 0, 1, 2, . . .
and:
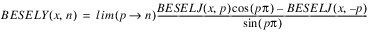
when n = 0, 1, 2, . . .
note | Under UNIX, BESELY uses the j0(3M), j1(3M), and jn(3M) functions from the UNIX math library. For details about these functions, refer to its UNIX man page. |
See Also
For a synopsis of all the Bessel functions, see Mathematical Handbook of Formulas and Tables, by Murray R. Spiegel, McGraw-Hill Book Company, New York, 1968.
For sample usage of the Bessel functions in physics, see Boundary Value Problems, Second Edition, edited by David L. Powers, Academic Press, New York, 1979, pp. 213-216.