ZEROS_FUNCTION Function
Finds the real zeros of a real, continuous, univariate function.
Usage
result = ZEROS_FUNCTION (fcn)
Input Parameters
fcn—User-supplied function, fcn ( x), to compute the value of the function of which the zeros will be found. Returns the computed function value at the point x.
x—The point at which the function is evaluated.
Returned Value
result—An array containing the zeros of the function. The zeros are in increasing order. If fewer than the requested number of zeros were found, the final entries are set to NaN. If there is a fatal error, then NULL is returned.
Input Keywords
Double—If present and nonzero, then double precision is used.
N_roots—A scalar long value indicating the number of zeros to be found. Default: N_roots = 1.
Bound—A two element array (a, b) indicating the closed interval in which to search for the roots. The function must be defined for all values in this interval. Default: The search for the roots is not bounded.
Max_evals—A scalar long value indicating the maximum number of function evaluations allowed. Once this limit is reached, the roots found are returned. Default: Max_evals = 100
Xguess—A 1D float array with N_roots components containing initial guesses for the zeros. If a bound on the zeros is also given, the guesses must satisfy the bound condition.
Err_abs—A scalar float value indicating the convergence criterion. A root is accepted if the absolute value of the function at the point is less than or equal to Err_abs. Default: Err_abs = 100 ε, where ε is the machine precision.
Err_x—A scalar float value indicating the convergence criterion. A root is accepted if it is bracketed within an interval of length Err_x. Default: Err_x = 100 ε / xscale, where ε is the machine precision.
Tolerance_muller—Müller’s method is started if, during refinement, a point is found for which the absolute value of the function is less than Tolerance_muller and the point is not near an already discovered root. If Tolerance_muller is less than or equal to zero, Müller’s method is never used. Default: Tolerance_muller = ε/Err_abs, where ε is the machine precision. With the default value of Err_abs, this equals 0.01.
Min_separation—A scalar float value indicating the minimum separation between accepted roots. If two points both satisfy the convergence criteria, but are within Min_separation of each other, only one of the roots is accepted. Default: Min_separation = ε1/2/Xscale, where ε is the machine precision.
Xscale—A scalar float value indicating the scaling in the x-coordinate. The absolute value of the roots divided by Xscale should be about one. Default: Xscale = 1.0
Output Keywords
Num_roots_found—A scalar long value indicating the number of zeros actually found.
N_evals—A scalar long value indicating the actual number of function evaluations used.
Discussion
The ZEROS_FUNCTION function computes N_roots real zeros of a real, continuous, univariate function. The search for the zeros of the function can be limited to a specified interval, or extended over the entire real line. The code is generally more efficient if an interval is specified. The user supplied function must return valid results for all values in the specified interval. If no interval is given, the user-supplied function must return valid results for all real numbers.
The function has two convergence criteria. The first criterion accepts a root, x, if:
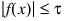
where τ = Err_x.
The second criterion accepts a root if it is known to be inside of an interval of length at most Err_abs.
A root is accepted if it satisfies either criteria and is not within Min_separation of another accepted root.
If initial guesses for the roots are given, Müller’s method (Müller 1956) is used for each of these guesses. For each guess, the Müller iteration is stopped if the next step would be outside of the bound, if given. The iteration is also stopped if it cannot make further progress in finding a root.
If no guess for the zeros were given, or if Müller’s method with the guesses did not find the requested number of roots, a meta-algorithm, combining Müller’s and Brent’s methods, is used. Müller’s method is used primarily to find the roots of functions, such as f(x) = x2, where the function does not cross the y=0 line. Brent’s method is used to find other types of roots.
The meta-algorithm successively refines the interval using a one-dimensional Faure low-discrepancy sequence. If the Bound keyword is used to specify a bounded interval, [a, b], the Faure sequence is scaled from (0,1) to (a,b).
If no bound on the function’s domain is given, the entire real line must be searched for roots. In this case, the Faure sequence is scaled from (0, 1) to (–∞, +∞) using the mapping:
h(u) = xscale * tan(π(u–1/2))
where xscale is given by the Xscale keyword.
At each step of the iteration the next point in the Faure sequence is added to the list of breakpoints defining the subintervals. Call the points x0=a, x1=b, x2, x3, .... The new point, xs, splits an existing subinterval, [xp, xq].
The function is evaluated at xs. If its value is small enough, specifically if:
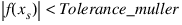
then Müller’s method is used with xp, xq and xs as starting values. If a root is found, it is added to the list of roots. If more roots are required, the new Faure point is used.
If Müller’s method did not find a root using the new point, the function value at the point is compared with the function values at the endpoints of the subinterval it divides. If f(xp)f(xs) < 0 and no root has previously been found in [xp, xs] then Brent’s method is used to find a root in this interval. Similarly, if the function changes sign over the interval [xs, xq], and a root has not already been found in the subinterval, Brent’s method is used there.
Example
This example finds a real zero of the function:
f(x) = ex – 3
and finds two real zeros of function:
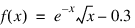
on the interval [0, 20].
FUNCTION z_fcn1, x
RETURN, EXP(x) - 3.0
END
FUNCTION z_fcn2, x
RETURN, SQRT(x)*EXP(-x) - 0.3
END
PRO zeros_function_ex1
x = ZEROS_FUNCTION("z_fcn1")PRINT," OUTPUT "
PRINT, "X(0) = ", X(0)
PRINT, "z_fcn1( X(0) ) = ", z_fcn1(x(0))
END
PRO zeros_function_ex2
n_roots = 2
bound = [0.0, 20.0]
x = ZEROS_FUNCTION("z_fcn2", $N_roots=n_roots, $
Num_roots_found=num_roots_found, $
Bound=bound)
PRINT," Num_roots_found = ", num_roots_found
PRINT," Root 1 = ", x(0)
PRINT," Root 2 = ", x(1)
PRINT,""
PRINT," Z_FCN2(x(0)) = ", Z_FCN2(x(0))
PRINT," Z_FCN2(x(1)) = ", Z_FCN2(x(1))
END
PRO t_zeros_function
PRINT, "EXAMPLE 1"
PRINT,"================="
zeros_function_ex1
PRINT,""
PRINT, "EXAMPLE 2"
PRINT,"================="
zeros_function_ex2
END
Output
EXAMPLE 1
=================
OUTPUT
X(0) = 1.09861
z_fcn1( X(0) ) = 0.00000
EXAMPLE 2
=================
Num_roots_found = 2
Root 1 = 0.112770
Root 2 = 1.35638
Z_FCN2(x(0)) = -2.98023e-08
Z_FCN2(x(1)) = 2.98023e-08
Warning Errors
IMSL_ZEROS_MAX_EVALS_EXCEEDED—The maximum number of function evaluations allowed has been exceeded. Any zeros found are returned.