GA_CHROMOSOME Function
Creates a data structure containing unencoded and encoded phenotype information.
Usage
result = GA_CHROMOSOME ( )
Returned Value
result—A data structure, which is required input to GA_INDIVIDUAL, GA_POPULATION, and GA_RANDOM_POPULATION.
Input Keywords
Double—If present and nonzero, then double precision is used.
Print—If present and nonzero, this option turns on printing of the summary results describing the chromosome structure. By default, summary results are not printed.
N_binary—The number of binary phenotypes. Default: N_binary = 0.
N_nominal—Scalar long value equal to the number of nominal phenotypes. Default: N_nominal = 0.
N_categories—Array of length N_nominal containing the number of nominal categories for each nominal phenotype. Each value of this array must be at least 2 or greater. If partially matched crossover (PMX) is used during the genetic algorithm search then the array N_categories is ignored since all of its values are assumed equal to N_nominal.
N_integer—Scalar long value equal to the number of integer phenotypes. Default: N_integer = 0.
I_intervals—A one-dimensional array of length N_integer containing the number of discrete intervals used to map each integer into the chromosome loci. For efficiency, each value in this array should be a power of 2 such as 2, 4, 8, 16, and so forth.
I_bounds—An array of size N_integer * 2 containing ordered lower and upper bounds pairs for each integer phenotype. The lower and upper bounds for the ith integer phenotype are equal to I_bounds(2i) and I_bounds(2i+1) respectively. Each integer value submitted to the GENETIC_ALGORITHM Function for the ith integer phenotype, wi, must conform to the inequality:
I_bounds(2i) ≤ wi ≤ I_bounds(2i + 1)
N_real—Scalar long value equal to the number of real phenotypes. Point values are mapped into chromosome loci using discretization. Default: N_real = 0.
R_intervals—A one-dimensional array of length N_real containing the number of discrete intervals used to map each real value into the chromosome loci. For efficiency, each value in this array should be a power of 2 such as 2, 4, 8, 16, and so forth.
R_bounds—An array of size N_real * 2 containing ordered lower and upper bounds pairs for each integer phenotype. The lower and upper bounds for the ith real phenotype are equal to R_bounds(2i) and R_bounds(2i + 1) respectively. Hence, R_bounds(2i + 1) must be greater than R_bounds(2i). Each real value submitted to the GENETIC_ALGORITHM Function for the ith real phenotype, wi, must conform to the inequality:
R_bounds(2i) ≤ wi ≤ R_bounds(2i + 1)
Double—If present and nonzero, then double precision is used.
Discussion
The genetic algorithm requires a chromosome representation of phenotypes. Most textbook applications of genetic algorithms use phenotypes that have a natural binary encoding. Real world problems often have non-binary phenotypes. Phenotypes are parameters used by the fitness function. Those can include any data type. This function allows for easy encoding of binary, nominal, integer and real phenotypes.
Binary phenotypes are mapped directly into the chromosome as binary bits. Each binary phenotype is treated as a single allele. If the user specifies N_binary > 0, then the first N_binary bits in the chromosome are allocated for encoding this information. When the fitness function is called during genetic optimization, these bits are translated into zeros and ones and then sent to the fitness function as an integer array of length N_binary.
Nominal phenotypes are mapped into the chromosome following the binary phenotypes. The number of bits assigned to each nominal phenotype is determined from the number of categories for each nominal phenotype. The value N_categories(i) is equal to the number of categories for the ith nominal phenotype. The number of bits assigned to this category is the smallest value of k such that 2k ≥ N_categories(i), i.e., k = ⎡log2(N_categories(i))⎤, where ⎡x⎤ is the ceiling of x (least integer of x). A binary nominal phenotype would be assigned one bit, and one bit would constitute a single allele. A trinary nominal phenotype would be assigned two bits since 22 = 4 ≥ 3, and these bits would be treated as a single allele.
The mapping of multiple bits to a single allele is a key difference between nominal phenotypes and other phenotypes. Alleles for binary, integer and real phenotypes are represented as single bits in the chromosome. The alleles for nominal phenotypes consist of multiple bits. Since crossover occurs between alleles, crossover for nominal phenotypes is treated differently. This ensures that only viable values for nominal phenotypes result from crossover.
It also means that Gray encoding of individual bits has no effect on nominal phenotypes. For many problems Gray encoding is used instead of standard Base-2 encoding to reduce large changes of encoded phenotype values after crossover. As a result, Gray encoding is never applied to nominal phenotypes.
In addition, partially mixed crossover is only an option for nominal phenotypes. Nominal phenotypes combined with partially mixed crossover make it easy to implement search problems similar to the traveling salesman problem.
Both integer and real phenotypes are discretized. Although this is the most common approach to encoding these phenotypes, some problems may benefit from other forms of encoding. If so, users should provide their own encoding, translating the phenotype into a bit representation that can be mapped into binary phenotypes.
Discretization is controlled by two arrays. For integer phenotypes, the array I_intervals contains the number of discrete intervals used to represent each integer. The number of chromosome bits assigned to the ith integer is determined by the values in this array. If I_intervals(i) = k = 2m then the ith integer phenotype is assigned m bits. For example, if I_intervals(i) = 4, then this phenotype is assigned two bits.
The array I_bounds contains the upper and lower bounds for each integer phenotype. The lower bound for the ith integer phenotype is equal to lb = I_bounds(2i), and the upper bound is equal to ub = I_bounds(2i + 1). The values for the ith phenotype, w, must satisfy the inequality lb ≤ w < ub. w is discretized to w' using the formula:

Where ⎣x⎦ is the floor of x (greatest integer of x). This results in mapping the ith integer phenotype, w, into one of the integers 0, 1, ..., k – 1.
Real phenotypes are handled in the same fashion as integer phenotypes using the values in R_intervals and R_bounds.
The number of chromosome bits assigned to each phenotype are described in the following table:
Phenotype | Number of Bits |
|---|---|
Binary | bbits = N_binary |
Nominal | 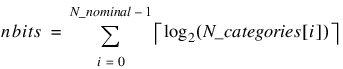 |
Integer | 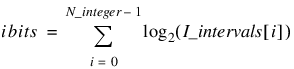 |
Real |  |
See Table 14-1: Chromosome Data Structure for a description of the allele values (bits) for the chromosome. Chromosome bits are ordered first by binary phenotypes in bits 0 through bbits – 1, then nominals, integers and reals in that order.
Example
This example creates a chromosome with 1 binary, 2 nominal, 3 integer and 2 real phenotypes. The Print keyword is used to print a description of the chromosome structure.
PRO ga_chromosome_ex1
n_binary = 1
n_nominal = 2
n_integer = 3
n_real = 2
; Number of categories for nominal phenotypes
n_categories = [2, 3]
; Number of intervals and boundaries for integer
; phenotypes
i_intervals = [16, 16, 16]
i_bounds = [0, 1000, -10, 10, -20, 0]
; Number of intervals and boundaries for real
; phenotypes
r_intervals = [512, 1024]
r_bounds = [0.0, 20.0, -20.0, 20.0]
chromosome = GA_CHROMOSOME( $
N_binary=n_binary, $
N_nominal=n_nominal, $
N_categories=n_categories, $
N_integer=n_integer, $
I_intervals=i_intervals, $
I_bounds=i_bounds, $
N_real=n_real, $
R_intervals=r_intervals, $
R_bounds=r_bounds, $
/Print)
END
Output
The Print keyword produced the following description of the chromosome. The data structure uses 304 bytes. The chromosome has 34 alleles. The first two are assigned to the nominal phenotypes. The first phenotype is encoded in allele 1 with the integers zero and one since it has only two categories. The second nominal phenotype has 3 categories. It is encoded with the integers zero, one, and two.
The third bit is used to represent the binary phenotype.
The integer phenotypes are each assigned 4 binary bits. Since the number of intervals is the same for each integer, 16, 4 bits is used to encode the integers 0-15. If Base-2 encoding is used, the 16th interval is encoded as 15 = {1111}.
The first real phenotype uses 512 intervals to discretize its value. This is encoded using 9 alleles. The second real phenotype uses 1024 intervals to discretize its value. This requires 10 alleles to properly represent the values 0 to 1023.
*******************************
**** CHROMOSOME STRUCTURE *****
Data Structure length: 304 Bytes
Chromosome length: 34 Bits
******ALLELE ASSIGNMENTS*******
Binary: 0 - 0 n_binary = 1
Nominal: 1 - 2 n_nominal= 2
Integer: 3 - 14 n_integer= 3
Real: 15 - 33 n_real = 2
*******************************
NOMINAL CATEGORIES*************
Variable 0: 2 categories
Variable 1: 3 categories
*******************************
INTEGER BOUNDS*****************
Variable 0: [ 0, 1000]
Variable 1: [ -10, 10]
Variable 2: [ -20, 0]
*******************************
INTEGER BITS*******************
Variable 0: 4 bits
Variable 1: 4 bits
Variable 2: 4 bits
*******************************
INTEGER DISCRETE INTERVALS*****
Variable 0: 16 intervals
Variable 1: 16 intervals
Variable 2: 16 intervals
*******************************
REAL BOUNDS********************
Variable 0: [0,20]
Variable 1: [-20,20]
*******************************
REAL BITS**********************
Variable 0: 9 bits
Variable 1: 10 bits
*******************************
REAL DISCRETE INTERVALS********
Variable 0: 512 intervals
Variable 1: 1024 intervals
*******************************