FEYNMAN_KAC Function
This function solves the generalized Feynman-Kac PDE on a rectangular grid using a finite element Galerkin method. Initial and boundary conditions are satisfied. The solution is represented by a series of C2 Hermite quintic splines.
Usage
result = FEYNMAN_KAC (nlbcd, nrbcd, xgrid, tgrid, fcn_fkcfiv, fcn_fkbcp, y, y_prime)
Input Parameters
nlbcd—A scalar long value indicating the number of left boundary conditions. It is required that 1 ≤ nlbcd ≤ 3.
nrbcd—A scalar long value indicating the number of right boundary conditions. It is required that 1 ≤ nrbcd ≤ 3.
xgrid—Array of length nxgrid containing the breakpoints for the Hermite quintic splines used in the x discretization, where nxgrid is the number of grid lines in the x-direction. The points in xgrid must be strictly increasing. The values xgrid(0) and xgrid(nxgrid – 1) are the endpoints of the interval.
tgrid—Array of length ntgrid containing the set of time points (in time-remaining units) where an approximate solution is returned. The points in tgrid must be positive and strictly increasing.
fcn_fkcfiv—User-supplied function, fcn_fkcfiv ( x, t, iflag, value), to compute the values of the coefficients σ, σ', μ, κ for the Feynman-Kac PDE and the initial data function p(x), xmin ≤ x ≤ xmax.
x—Space variable.
t—Time variable.
iflag—On entry, iflag indicates which coefficient or data function is to be computed. The following table shows which value has to be returned by fcn_fkcfiv for all possible values of iflag:
iflag | Computed coefficient | |
|---|---|---|
–1 | 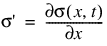 | |
0 | p(x) | |
1 | σ | |
2 | μ | |
3 | κ |
For non-zero input values of iflag, note when a coefficient does not depend on t. This is done by setting iflag = 0 after the coefficient is defined. If there is time dependence, the value of iflag should not be changed. This action will usually yield a more efficient algorithm because some finite element matrices do not have to be reassembled for each t value.
value—Value of the coefficient or initial data function. Which value is computed depends on the input value for iflag.
fcn_fkbcp—User-supplied function, fcn_fkbcp ( nbc, t, iflag, values), to define boundary values that the solution of the differential equation must satisfy. There are nlbcd conditions specified at the left end, xmin, and nrbcd conditions at the right end, xmax. The boundary conditions are:
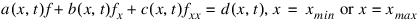
nbc—Number of boundary conditions. At xmin, nbc=nlbcd, at xmax, nbc = nrbcd.
t—Time point of the boundary conditions.
iflag—On entry, iflag indicates whether the coefficients for the left or right boundary conditions are to be computed:
iflag | Computed boundary conditions | |
|---|---|---|
1 | Left end, x = xmin | |
2 | Right end, x = xmax |
If there is no time dependence for one of the boundaries then set iflag = 0 after the array values is defined for either end point. This flag can avoid unneeded continued computation of the finite element matrices.
values—Array of length 4*max(nlbcd, nrbcd) containing the values of the boundary condition coefficients in its first 4*nbc locations. The coefficients for xmin are stored row-wise according to the following scheme:
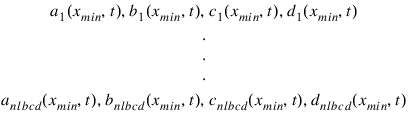
The coefficients for xmax are stored similarly.
Output Parameters
y—An array of size (ntgrid+1) by (3*nxgrid) containing the coefficients of the Hermite representation of the approximate solution for the Feynman-Kac PDE at time points 0, tgrid(0), ..., tgrid(ntgrid–1). The approximate solution is given by:
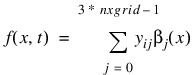 for t = tgrid(i–1), i = 1, ..., ntgrid.
for t = tgrid(i–1), i = 1, ..., ntgrid. The representation for the initial data at t = 0 is:
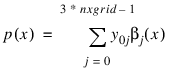
The (ntgrid+1) by (3*nxgrid) matrix:
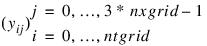
is stored row-wise in array y.
After the integration, use row i of array y as input argument coef in function FEYNMAN_KAC_EVALUATE Function to obtain an array of values for f(x, t) or its partials fx, fxx, fxxx at time point t=0, tgrid(i–1), i=1, ..., ntgrid.
The expressions for the basis functions βj(x) are represented piece-wise and can be found in Hanson, R. (2008) “Integrating Feynman-Kac Equations Using Hermite Quintic Finite Elements”.
y_prime—An array of size (ntgrid + 1) by (3*nxgrid) containing the first derivatives of y at time points 0, tgrid(0), ..., tgrid(ntgrid – 1), i.e.
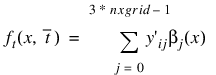 for
for 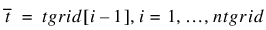
and:
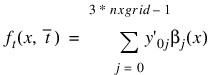 for
for 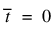
The (ntgrid + 1) by (3*nxgrid) matrix:
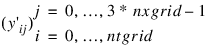
is stored row-wise in array y_prime.
After the integration, use row i of array y_prime as input argument coef in function FEYNMAN_KAC_EVALUATE to obtain an array of values for the partials ft, ftx, ftxx, ftxxx 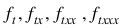 at time point t=tgrid(i–1), i=1, ..., ntgrid and row 0 for the partials at t=0.
at time point t=tgrid(i–1), i=1, ..., ntgrid and row 0 for the partials at t=0.
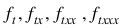 at time point t=tgrid(i–1), i=1, ..., ntgrid and row 0 for the partials at t=0.
at time point t=tgrid(i–1), i=1, ..., ntgrid and row 0 for the partials at t=0.Returned Value
result—This function returns 1 to indicate success.
Input Keywords
Double—If present and nonzero, then double precision is used.
Fcn_fkinit—User-supplied function, Fcn_fkinit(nxgrid, ntgrid, xgrid, tgrid, time, yprime, y, atol, rtol), for adjustment of initial data or as an opportunity for output during the integration steps. The solution values of the model parameters are presented in the arrays y and yprime at the integration points time = 0, tgrid(j), j=0,...,ntgrid–1. At the initial point, integral least-squares estimates are made for representing the initial data p(x). If this is not satisfactory, fcn_fkinit can change the contents of y to match data for any reason.
nxgrid—Number of grid lines in the x-direction.
ntgrid—Number of time points where an approximate solution is returned.
xgrid—Vector of length nxgrid containing the breakpoints for the Hermite quintic splines used in the x discretization.
tgrid—Vector of length ntgrid containing the set of time points (in time-remaining units) where an approximate solution is returned.
time—Time variable.
yprime—Vector of length 3*nxgrid containing the derivative of the coefficients of the Hermite quintic spline at time point time.
y—Vector of length 3*nxgrid containing the coefficients of the Hermite quintic spline at time point time.
atol—Array of length 3*nxgrid containing absolute error tolerances.
rtol—Array of length 3*nxgrid containing relative error tolerances.
Fcn_force—User-supplied function, Fcn_force(interval, ndeg, nxgrid, y, time, width, xlocal, qw, u, phi, dphi), used in case there is a non-zero term φ(f,x,t) in the Feynman-Kac differential equation. If function Fcn_force is not used, it is assumed that φ(f,x,t) is identically zero.
interval—Index indicating the bounds xgrid(interval–1) and xgrid(interval) of the integration interval, 1 ≤ interval ≤ nxgrid–1.
ndeg—The degree used for the Gauss-Legendre formulas.
nxgrid—Number of grid lines in the x-direction.
y—Vector of length 3*nxgrid containing the coefficients of the Hermite quintic spline representing the solution of the Feynman-Kac equation at time point time.
time—Time variable.
width—The interval width, width = xgrid(interval) – xgrid(interval–1).
xlocal—Array of length ndeg containing the Gauss-Legendre points translated and normalized to the interval [xgrid(interval–1), xgrid(interval)].
qw—Vector of length ndeg containing the Gauss-Legendre weights.
u—Array of dimension 12 by ndeg containing the basis function values that define 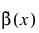 at the Gauss-Legendre points xlocal. Setting
at the Gauss-Legendre points xlocal. Setting
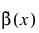 at the Gauss-Legendre points xlocal. Setting
at the Gauss-Legendre points xlocal. Setting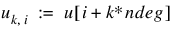 and
and 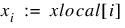 ,
, 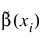 is defined as:
is defined as: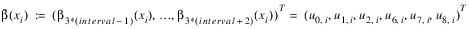
phi—Vector of length 6 containing Gauss-Legendre approximations for the local contributions:
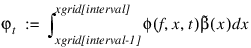
where t = time and:
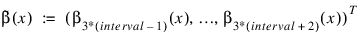
Vector phi contains elements:
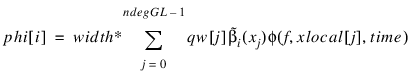
for i=0, ..., 5.
dphi—Array of dimension 6 by 6 containing a Gauss-Legendre approximation for the Jacobian of the local contributions ϕt at t = time:
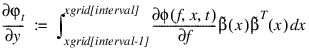
The approximation to this symmetric matrix is stored row-wise, i.e.:
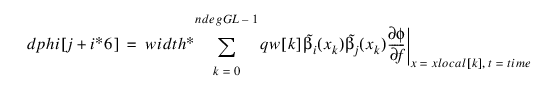
for i,j=0, ..., 5.
ScalarAtolRtol—Scalar values that apply to the error estimates of all components of the solution y in the differential equation solver SDASLX. See the Atol and Rtol keywords if separate tolerances are to be applied to each component of y. Default: Atol and Rtol are set to 10–3 in single precision and 10–5 in double precision.
Atol—Componentwise tolerances are used for the computation of solution y in the differential equation solver SDASLX. Atol is an array of length 3*nxgrid to be used for the absolute and relative tolerance and to be applied to each component of the solution, y. See keyword Atolrtolscalars if scalar values of absolute and relative tolerances are to be applied to all components. Default: All elements of Atol and Rtol are set to 10–3 in single precision and 10–5 in double precision.
Rtol—Componentwise tolerances are used for the computation of solution y in the differential equation solver SDASLX. Rtol is an array of length 3*nxgrid to be used for the absolute and relative tolerance and to be applied to each component of the solution, y. See keyword Atolrtolscalars if scalar values of absolute and relative tolerances are to be applied to all components. Default: All elements of Atol and Rtol are set to 10–3 in single precision and 10–5 in double precision.
Ndeg—The degree used for the Gauss-Legendre formulas for constructing the finite element matrices. It is required that Ndeg ≥ 6. Default: Ndeg = 6.
Tdepend—Vector of length 7 indicating time dependence of the coefficients, boundary conditions and function φ in the Feynman-Kac equation. If tdepend(i) = 0 then argument i is not time dependent, if tdepend(i)=1 then argument i is time dependent.
i | time dependence of variable |
|---|---|
0 | σ' |
1 | σ |
2 | μ |
3 | κ |
4 | Left boundary conditions |
5 | Right boundary conditions |
6 | φ |
Max_stepsize—This is the maximum step size the integrator may take. Default: Max_stepsize = MACHINE(MAX_POS), the largest possible machine number.
Init_stepsize—The starting step size for the integration. Must be less than zero since the integration is internally done from t=0 to t=tgrid(ntgrid–1) in a negative direction. Default: Init_stepsize = –ε, where ε is the machine precision
Max_Nsteps—The maximum number of steps between each output point of the integration. Default: Max_Nsteps = 500000.
Step_control—Indicates which step control algorithm is used for the integration. If Step_control = 0, then the step control method of Söderlind is used. If Step_control = 1, then the method used by the original Petzold code SASSL is used. Default: Step_control = 0.
Max_bdf_order—Maximum order of the backward differentiation formulas used in the integrator. It is required that 1 ≤ Max_bdf_order ≤ 5. Default: Max_bdf_order = 5.
T_barrier—This keyword controls whether the code should integrate past a special point, T_barrier, and then interpolate to get y and y' at the points in tgrid. If this keyword is present, the integrator assumes the equations either change on the alternate sides of T_barrier or they are undefined there. In this case, the code creeps up to T_barrier in the direction of integration. It is required that T_barrier ≥ tgrid(ntgrid–1). Default: T_barrier = tgrid(ntgrid–1).
Output Keywords
Istate—An array of length 7 whose entries flag the state of computation for the matrices and vectors required in the integration. For each entry, a zero indicates that no computation has been done or there is a time dependence. A one indicates that the entry has been computed and there is no time dependence. The Istate entries are as follows:
i | Entry in istate |
|---|---|
0 | Mass Matrix, M |
1 | Stiffness matrix, N |
2 | Bending matrix, R |
3 | Weighted mass, K |
4 | Left boundary condition data |
5 | Right boundary condition data |
6 | Forcing term |
Default: Istate(i) = 0 for i = 0, ..., 6.
Nval—Array of length 3 summarizing the number of evaluations required during the integration.
i | nval(i) |
|---|---|
0 | Number of residual function evaluations of the DAE used in the model. |
1 | Number of factorizations of the differential matrix associated with solving the DAE. |
2 | Number of linear system solve steps using the differential matrix. |
Discussion
The generalized Feynman-Kac differential equation has the form
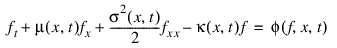
where the initial data satisfies f(x, T) = p(x). The derivatives are 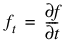 , etc. The FEYNMAN_KAC function uses a finite element Galerkin method over the rectangle:
, etc. The FEYNMAN_KAC function uses a finite element Galerkin method over the rectangle:
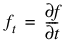 , etc. The FEYNMAN_KAC function uses a finite element Galerkin method over the rectangle:
, etc. The FEYNMAN_KAC function uses a finite element Galerkin method over the rectangle: 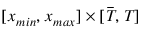
in (x, t) to compute the approximate solution. The interval [xmin, xmax] is decomposed with a grid:
(xmin =)x1 < x2 < ... < xm (= xmax)
On each subinterval the solution is represented by:
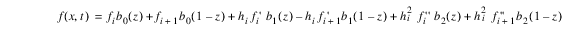
The values:
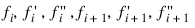
are time-dependent coefficients associated with each interval. The basis functions b0, b1, b2 are given for:
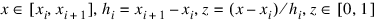
by:
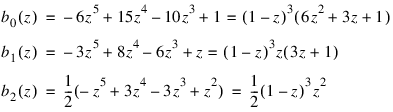
The Galerkin principle is then applied. Using the provided initial and boundary conditions leads to an Index 1 differential-algebraic equation for the time-dependent coefficients:
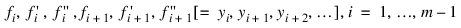
This system is integrated using the variable order, variable step algorithm DDASLX/SDASLX noted in Hanson and Krogh, R. (2008) Solving Constrained Differential-Algebraic Systems Using Projections. Solution values and their time derivatives are returned at a grid preceding time T, expressed in units of time remaining. For further details of deriving and solving the system see Hanson, R. (2008) Integrating Feynman-Kac Equations Using Hermite Quintic Finite Elements. To evaluate f or its partial derivatives at any time point in the grid, use the FEYNMAN_KAC_EVALUATE Function.
Example 1
The value of the American Option on a Vanilla Put can be no smaller than its European counterpart. That is due to the American Option providing the opportunity to exercise at any time prior to expiration. This example compares this difference—or premium value of the American Option—at two time values using the Black-Scholes model. The example is based on Wilmott et al. (1996, p. 176), and uses the non-linear forcing or weighting term described in Hanson, R. (2008), “Integrating Feynman-Kac Equations Using Hermite Quintic Finite Elements”, for evaluating the price of the American Option. The coefficients, payoff, boundary conditions and forcing term for American and European options are defined by the user functions fkcfiv_put, fkbcp_put and fkforce_put, respectively. One breakpoint is set exactly at the strike price.
The sets of parameters in the computation are:
1. Strike price K = {10.0}
2. Volatility σ = {0.4}
3. Times until expiration = {1/4, 1/2}
4. Interest rate r = 0.1
5. xmin = 0.0, xmax = 30.0
6. nx = 61, n = 3 × nx = 183
The payoff function is the “vanilla option”, p(x) = max(K – x, 0).
; These routines define the coefficients, payoff, boundary
; conditions and forcing term for American and European
; Options.
FUNCTION fkcfiv_put, x, tx, iflag, value
; The sigma value.
sigma=0.4
; Value of the interest rate and continuous dividend.
strike_price=10.0
interest_rate=0.1
dividend=0.0
zero=0.0
CASE iflag OF
0:BEGIN
; The payoff function.
value = MAX([strike_price - x, zero])
END
-1:BEGIN
; The coefficient derivative dsigma/dx.
value = sigma
END
1:BEGIN
; The coefficient sigma(x).
value = sigma*x
END
2:BEGIN
; The coefficient mu(x).
value = (interest_rate - dividend) * x
END
3:BEGIN
; The coefficient kappa(x).
value = interest_rate
END
ENDCASE
; Note that there is no time dependence.
iflag = 0L
RETURN,1
END
FUNCTION fkbcp_put, nbc, tx, iflag, val
CASE iflag OF
1:BEGIN
val(*) = 0.0
val(1) = 1.0
val(3) = -1.0
val(6) = 1.0
END
2:BEGIN
val(*) = 0.0
val(0) = 1.0
val(5) = 1.0
val(10) = 1.0
END
ENDCASE
; Note no time dependence.
iflag = 0
RETURN,1
END
FUNCTION fkforce_put, interval, ndeg, nxgrid, $
y, time, width, xlocal, $
qw, u, phi, dphi
COMMON f_kac_usr, usr_data
local=6
yl = FLTARR(local)
bf = FLTARR(local)
zero=0.0
one=1.0
index = INDGEN(local)
data = usr_data
yl = y(3*interval-3 + index)
phi(*) = zero
strike_price = data(0)
interest_rate = data(1)
value = data(2)
mu=2.0
; This is the local definition of the forcing term.
FOR j=1L, local DO BEGIN
FOR l=1L, ndeg DO BEGIN
bf(0) = u((l-1))
bf(1) = u((l-1)+ndeg)
bf(2) = u((l-1)+2*ndeg)
bf(3) = u((l-1)+6*ndeg)
bf(4) = u((l-1)+7*ndeg)
bf(5) = u((l-1)+8*ndeg)
rt = SUM(yl * bf)
rt = value/(rt + value - (strike_price-xlocal(l-1)))
phi(j-1) = phi(j-1) + (qw(l-1) * bf(j-1) * rt^mu)
ENDFOR
ENDFOR
phi = -phi * width*interest_rate*strike_price
; This is the local derivative matrix for the forcing term.
dphi(*) = zero
FOR j=1L, local DO BEGIN
FOR i=1L, local DO BEGIN
FOR l=1L, ndeg DO BEGIN
bf(0) = u((l-1))
bf(1) = u((l-1)+ndeg)
bf(2) = u((l-1)+2*ndeg)
bf(3) = u((l-1)+6*ndeg)
bf(4) = u((l-1)+7*ndeg)
bf(5) = u((l-1)+8*ndeg)
rt = SUM(yl * bf)
rt = one/(rt + value-(strike_price-xlocal(l-1)))
dphi(i-1+(j-1)*local) = dphi(i-1+(j-1)*local) + $
qw(l-1) * bf(i-1) * bf(j-1) $
* (rt^(mu+1.0))
ENDFOR
ENDFOR
ENDFOR
FOR i=0L, (local*local)-1 DO BEGIN
dphi(i) = mu * dphi(i) * width * value^mu * $
interest_rate * strike_price
ENDFOR
RETURN,1
END
PRO feynman_kac_ex1
; Compute American Option Premium for Vanilla Put.
COMMON f_kac_usr, usr_data
NXGRD = 61
NTGRD = 2
NV = 9
; The strike price.
KS = 10.0
; The sigma value.
sigma = 0.4
; Time values for the options.
nt = 2
time = [ 0.25, 0.5]
; Values of the underlying where evaluations are made.
xs = [ 0.0, 2.0, 4.0, 6.0, 8.0, 10.0, $
12.0, 14.0, 16.0 ]
; Value of the interest rate.
r = 0.1
; Values of the min and max underlying values modeled.
x_min=0.0
x_max=30.0
; Define parameters for the integration step.
nint=NXGRD-1
n=3*NXGRD
xgrid = FLTARR(NXGRD)
ye = FLTARR((NTGRD+1),3*NXGRD)
yeprime = FLTARR((NTGRD+1),3*NXGRD)
ya = FLTARR((NTGRD+1),3*NXGRD)
yaprime = FLTARR((NTGRD+1),3*NXGRD)
fe = FLTARR(NTGRD*NV)
fa = FLTARR(NTGRD*NV)
dx = 0.0
nlbcd = 2
nrbcd = 3
atol = 0.2e-2
; Array for user-defined data.
usr_data = FLTARR(3)
; Define an equally-spaced grid of points for the
; underlying price.
;
; Determine the increment between points (to be used later...)
dx = (x_max-x_min)/ nint
; Create the grid.
xgrid = INTERPOL([x_min,x_max], NXGRD)
Atol_Rtol = [ 0.5e-2, 0.5e-2 ]
; Set up the user data in the COMMON block for the user
; function(s).
usr_data = [KS, r, atol]
ret = FEYNMAN_KAC(nlbcd, nrbcd, xgrid, time, $
"fkcfiv_put", "fkbcp_put", ye, yeprime, $
ScalarAtolRtol=Atol_Rtol)
ret = FEYNMAN_KAC(nlbcd, nrbcd, xgrid, time, $
"fkcfiv_put", "fkbcp_put", ya, $
yaprime, Fcn_force="fkforce_put" , $
ScalarAtolRtol=Atol_Rtol)
; Evaluate solutions at vector of points XS(:), at each
; time value prior to expiration.
FOR i=0L, nt-1 DO BEGIN
fe(i*NV:(i*NV)+NV-1) = FEYNMAN_KAC_EVALUATE(xgrid, $
xs, ye((i+1),*))
fa(i*NV:(i*NV)+NV-1) = FEYNMAN_KAC_EVALUATE(xgrid, xs, $
ya((i+1),*))
ENDFOR
PRINT,'American Option Premium for Vanilla Put, ' + $
'3 and 6 Months Prior to Expiry'
PRINT," Number of equally spaced spline knots: ", NXGRD
PRINT," Number of unknowns: ", n
PRINT," Strike=",KS," sigma=",sigma," Interest Rate=",r
PRINT,""
PRINT,"Underlying European American"
FOR i=0L, NV-1 DO BEGIN
PRINT, xs(i), fe(i), fe(i+NV), fa(i), fa(i+NV), $
format='(5(f10.4))'
ENDFOR
PRINT,""
END
Output
American Option Premium for Vanilla Put, 3 and 6 Months Prior to Expiry
Number of equally spaced spline knots: 61
Number of unknowns: 183
Strike= 10.0000, sigma= 0.400000, Interest Rate= 0.100000
Underlying European American
0.0000 9.7536 9.5134 10.0000 10.0000
2.0000 7.7537 7.5135 8.0000 8.0000
4.0000 5.7538 5.5150 6.0000 6.0000
6.0000 3.7619 3.5664 4.0000 4.0000
8.0000 1.9073 1.9170 2.0146 2.0880
10.0000 0.6518 0.8579 0.6768 0.9042
12.0000 0.1628 0.3392 0.1679 0.3526
14.0000 0.0374 0.1271 0.0374 0.1321
16.0000 0.0091 0.0477 0.0085 0.0499
Example 2
In Beckers (1980) there is a model for a Stochastic Differential Equation of option pricing. The idea is a “ constant elasticity of variance diffusion (or CEV) class”:
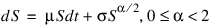
The Black-Scholes model is the limiting case α → 2. A numerical solution of this diffusion model yields the price of a call option. Various values of the strike price K, time values, σ and power coefficient α are used to evaluate the option price at values of the underlying price. The sets of parameters in the computation are:
1. power α = {2.0, 1.0, 0.0}
2. strike price K = {15.0, 20.0, 25.0}
3. volatility σ = {0.2, 0.3, 0.4}
4. times until expiration = {1/12, 4/12, 7/12}
5. underlying prices = {19.0, 20.0, 21.0}
6. interest rate r = 0.05
7. xmin = 0, xmax = 60
8. nx = 121, n = 3 × nx = 363
With this model the Feynman-Kac differential equation is defined by identifying:
x: S
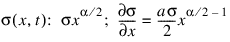
μ(x,t): rx
κ(x,t): r
φ(f,x,t) ≡ 0
The payoff function is the “vanilla option”, p(x) = max(x – K, 0).
FUNCTION fcn_fkcfiv, x, tx, iflag, value
COMMON f_kac_usr, usr_data
zero=0.0
half=0.5
data = usr_data
strike_price = data(0)
sigma = data(2)
alpha = data(3)
interest_rate = data(4)
dividend = data(5)
CASE iflag OF
0:BEGIN
; The payoff function.
value = (x - strike_price)>zero
END
-1:BEGIN
; The coefficient derivative d sigma/ dx.
value = half * alpha * sigma * x^(alpha*half-1.0)
END
1:BEGIN
; The coefficient sigma(x).
value = sigma * x^(alpha*half)
END
2:BEGIN
; The coefficient mu(x).
value = (interest_rate - dividend) * x
END
3:BEGIN
; The coefficient kappa(x).
value = interest_rate
END
ENDCASE
; Note that there is no time dependence.
iflag = 0
RETURN,1
END
FUNCTION fcn_fkbcp, nbc, tx, iflag, val
COMMON f_kac_usr, usr_data
data = usr_data
strike_price = data(0)
x_max = data(1)
interest_rate = data(4)
CASE iflag OF
1:BEGIN
val(*) = 0.0
val(0) = 1.0
val(5) = 1.0
val(10) = 1.0
; Note no time dependence at left end.
iflag = 0
END
2:BEGIN
df = EXP(interest_rate*tx)
val(*) = 0.0
val(0) = 1.0
val(3) = x_max - df*strike_price
val(5) = 1.0
val(7) = 1.0
val(10) = 1.0
END
ENDCASE
RETURN,1
END
PRO t_feynman_kac_ex2
COMMON f_kac_usr, usr_data
NXGRD = 121l
NTGRD = 3l
NV = 3l
; Compute Constant Elasticity of Variance Model for Vanilla Call
; The set of strike prices.
KS= [ 15.0, 20.0, 25.0]
; The set of sigma values.
sigma = [ 0.2, 0.3, 0.4]
; The set of model diffusion powers.
alpha = [2.0, 1.0, 0.0]
; Time values for the options.
nt = NTGRD
time = [ 1.0/12.0, 4.0/12.0, 7.0/12.0 ]
; Values of the underlying where evaluations are made.
xs = [ 19.0, 20.0, 21.0 ]
; Value of the interest rate and continuous dividend.
r=0.05
dividend=0.0
; Values of the min and max underlying values modeled.
x_min=0.0
x_max=60.0
; Define parameters for the integration step.
nint = NXGRD-1
n = 3*NXGRD
xgrid = FLTARR(NXGRD)
y = FLTARR((NTGRD+1)*3*NXGRD)
yprime = FLTARR((NTGRD+1)*3*NXGRD)
f = FLTARR(NTGRD*NV)
dx = 0.0
; Number of left/right boundary conditions.
nlbcd = 3L
nrbcd = 3L
usr_data = FLTARR(6)
; Define equally-spaced grid of points for the underlying price.
xgrid = INTERPOL([x_min,x_max], NXGRD)
PRINT,"Constant Elasticity of Variance Model for Vanilla Call"
PRINT,"Interest Rate: ",r," Continuous Dividend: ", dividend
PRINT,"Minimum and Maximum Prices of Underlying: ", $
STRING(x_min,Format="(f6.2)"), " ",$
STRING(x_max ,Format="(f6.2)")
PRINT,"Number of equally spaced spline knots:",NXGRD-1
PRINT,"Number of unknowns:",n
PRINT,""
PRINT,"Time in Years Prior to Expiration: ", $
STRING(time(0),Format="(f7.4)"), " ",$
STRING(time(1),Format="(f7.4)"), " ",$
STRING(time(2),Format="(f7.4)")
PRINT,"Option valued at Underlying Prices: ", $
STRING(xs(0),Format="(f5.2)"), " ",$
STRING(xs(1),Format="(f5.2)"), " ",$
STRING(xs(2),Format="(f5.2)")
PRINT,""
FOR i1=1L, 3 DO BEGIN ; Loop over power.
FOR i2=1L, 3 DO BEGIN ; Loop over volatility.
FOR i3=1L, 3 DO BEGIN ; Loop over strike price.
; Pass data through into evaluation routines.
usr_data(0) = KS(i3-1)
usr_data(1) = x_max
usr_data(2) = sigma(i2-1)
usr_data(3) = alpha(i1-1)
usr_data(4) = r
usr_data(5) = dividend
ret = FEYNMAN_KAC(nlbcd, nrbcd, xgrid, time, $
"fcn_fkcfiv", "fcn_fkbcp", y, yprime)
; Evaluate solution at vector of points xs, at each
; time Value prior to expiration.
FOR i=0L, NTGRD-1 DO $
f(i*NV:(i*NV)+NV-1) = $
FEYNMAN_KAC_EVALUATE(xgrid, xs, REFORM(y((i+1),*)))
outstr = "Strike="+STRING(KS(i3-1),Format="(f6.2)")+ $
" Sigma="+STRING(sigma(i2-1),Format="(f6.2)")+ $
" Alpha="+STRING(alpha(i1-1),Format="(f6.2)")
PRINT, outstr
FOR i=0L, NV-1 DO BEGIN
outstr = " Call Option Values "+ $
STRING(f(i),Format="(f7.4)") + " "+ $
STRING(f(NV+i),Format="(f7.4)") + " "+ $
STRING(f(2*NV+i),Format="(f7.4)")
PRINT, outstr
ENDFOR
ENDFOR
ENDFOR
ENDFOR
END
Output
Constant Elasticity of Variance Model for Vanilla Call
Interest Rate: 0.0500000 Continuous Dividend: 0.00000
Minimum and Maximum Prices of Underlying: 0.00 60.00
Number of equally spaced spline knots: 120
Number of unknowns: 363
Time in Years Prior to Expiration: 0.0833 0.3333 0.5833
Option valued at Underlying Prices: 19.00 20.00 21.00
Strike= 15.00 Sigma= 0.20 Alpha= 2.00
Call Option Values 4.0624 4.2575 4.4729
Call Option Values 5.0624 5.2506 5.4490
Call Option Values 6.0624 6.2486 6.4385
Strike= 20.00 Sigma= 0.20 Alpha= 2.00
Call Option Values 0.1310 0.5956 0.9698
Call Option Values 0.5029 1.0889 1.5100
Call Option Values 1.1980 1.7484 2.1751
Strike= 25.00 Sigma= 0.20 Alpha= 2.00
Call Option Values 0.0000 0.0113 0.0744
Call Option Values 0.0000 0.0373 0.1615
Call Option Values 0.0007 0.1026 0.3132
Strike= 15.00 Sigma= 0.30 Alpha= 2.00
Call Option Values 4.0639 4.3397 4.6618
Call Option Values 5.0626 5.2945 5.5783
Call Option Values 6.0624 6.2709 6.5238
Strike= 20.00 Sigma= 0.30 Alpha= 2.00
Call Option Values 0.3109 1.0275 1.5500
Call Option Values 0.7323 1.5422 2.1024
Call Option Values 1.3765 2.1690 2.7385
Strike= 25.00 Sigma= 0.30 Alpha= 2.00
Call Option Values 0.0006 0.1111 0.3542
Call Option Values 0.0037 0.2169 0.5547
Call Option Values 0.0182 0.3857 0.8222
Strike= 15.00 Sigma= 0.40 Alpha= 2.00
Call Option Values 4.0755 4.5138 4.9674
Call Option Values 5.0661 5.4201 5.8324
Call Option Values 6.0634 6.3578 6.7298
Strike= 20.00 Sigma= 0.40 Alpha= 2.00
Call Option Values 0.5116 1.4645 2.1292
Call Option Values 0.9623 1.9957 2.6951
Call Option Values 1.5815 2.6110 3.3236
Strike= 25.00 Sigma= 0.40 Alpha= 2.00
Call Option Values 0.0083 0.3284 0.7785
Call Option Values 0.0284 0.5165 1.0654
Call Option Values 0.0812 0.7686 1.4104
Strike= 15.00 Sigma= 0.20 Alpha= 1.00
Call Option Values 4.0624 4.2479 4.4312
Call Option Values 5.0624 5.2479 5.4312
Call Option Values 6.0624 6.2479 6.4312
Strike= 20.00 Sigma= 0.20 Alpha= 1.00
Call Option Values 0.0000 0.0226 0.1049
Call Option Values 0.1495 0.4107 0.6485
Call Option Values 1.0832 1.3314 1.5773
Strike= 25.00 Sigma= 0.20 Alpha= 1.00
Call Option Values 0.0000 -0.0000 0.0000
Call Option Values -0.0000 -0.0000 0.0000
Call Option Values -0.0000 0.0000 0.0000
Strike= 15.00 Sigma= 0.30 Alpha= 1.00
Call Option Values 4.0624 4.2479 4.4312
Call Option Values 5.0624 5.2479 5.4312
Call Option Values 6.0624 6.2479 6.4312
Strike= 20.00 Sigma= 0.30 Alpha= 1.00
Call Option Values 0.0016 0.0785 0.2204
Call Option Values 0.1979 0.4997 0.7541
Call Option Values 1.0836 1.3443 1.6022
Strike= 25.00 Sigma= 0.30 Alpha= 1.00
Call Option Values -0.0000 0.0000 0.0000
Call Option Values -0.0000 0.0000 0.0000
Call Option Values -0.0000 0.0000 0.0005
Strike= 15.00 Sigma= 0.40 Alpha= 1.00
Call Option Values 4.0624 4.2477 4.4310
Call Option Values 5.0624 5.2477 5.4309
Call Option Values 6.0624 6.2477 6.4309
Strike= 20.00 Sigma= 0.40 Alpha= 1.00
Call Option Values 0.0084 0.1542 0.3443
Call Option Values 0.2482 0.5943 0.8729
Call Option Values 1.0871 1.3790 1.6584
Strike= 25.00 Sigma= 0.40 Alpha= 1.00
Call Option Values 0.0000 0.0000 0.0001
Call Option Values 0.0000 0.0000 0.0008
Call Option Values 0.0000 0.0004 0.0066
Strike= 15.00 Sigma= 0.20 Alpha= 0.00
Call Option Values 4.0627 4.2478 4.4312
Call Option Values 5.0623 5.2479 5.4311
Call Option Values 6.0623 6.2479 6.4312
Strike= 20.00 Sigma= 0.20 Alpha= 0.00
Call Option Values 0.0001 0.0001 0.0002
Call Option Values 0.0816 0.3316 0.5748
Call Option Values 1.0818 1.3308 1.5748
Strike= 25.00 Sigma= 0.20 Alpha= 0.00
Call Option Values 0.0000 -0.0000 -0.0000
Call Option Values 0.0000 -0.0000 -0.0000
Call Option Values -0.0000 0.0000 -0.0000
Strike= 15.00 Sigma= 0.30 Alpha= 0.00
Call Option Values 4.0625 4.2479 4.4312
Call Option Values 5.0623 5.2479 5.4312
Call Option Values 6.0624 6.2479 6.4312
Strike= 20.00 Sigma= 0.30 Alpha= 0.00
Call Option Values 0.0000 -0.0000 0.0029
Call Option Values 0.0895 0.3326 0.5753
Call Option Values 1.0826 1.3306 1.5749
Strike= 25.00 Sigma= 0.30 Alpha= 0.00
Call Option Values 0.0000 -0.0000 0.0000
Call Option Values 0.0000 -0.0000 -0.0000
Call Option Values 0.0000 -0.0000 -0.0000
Strike= 15.00 Sigma= 0.40 Alpha= 0.00
Call Option Values 4.0624 4.2479 4.4312
Call Option Values 5.0623 5.2479 5.4312
Call Option Values 6.0624 6.2479 6.4312
Strike= 20.00 Sigma= 0.40 Alpha= 0.00
Call Option Values -0.0000 0.0001 0.0111
Call Option Values 0.0985 0.3383 0.5781
Call Option Values 1.0830 1.3306 1.5749
Strike= 25.00 Sigma= 0.40 Alpha= 0.00
Call Option Values 0.0000 0.0000 0.0000
Call Option Values 0.0000 -0.0000 0.0000
Call Option Values 0.0000 -0.0000 0.0000
Example 3
This example evaluates the price of a European Option using two payoff strategies: Cash-or-Nothing and Vertical Spread. In the first case the payoff function is:
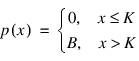
The value B is regarded as the bet on the asset price, see Wilmott et al. (1995, p. 39-40). The second case has the payoff function:
p(x) = max(x – K1) – max(x – K2), K2 > K1
Both problems use the same boundary conditions. Each case requires a separate integration of the Black-Scholes differential equation, but only the payoff function evaluation differs in each case. The sets of parameters in the computation are:
1. Strike and bet prices K1={10.0}, K2 = {15.0}, and B = {2.0}
2. Volatility σ = {0.4}
3. Times until expiration = {1/4, 1/2}
4. Interest rate r = 0.1.
5. xmin = 0, xmax = 30
6. nx = 61, n = 3 × nx = 183
PRO t_feynman_kac_ex3
COMMON f_kac_usr, usr_data
NXGRD = 61l
NTGRD = 2l
NV = 12l
; The strike price.
KS1 = 10.0
; The spread value.
KS2 = 15.0
; The Bet for the Cash-or-Nothing Call.
bet = 2.0
; The sigma value.
sigma = 0.4
; Time values for the options.
time = [0.25, 0.5]
; Values of the underlying where evaluations are made.
xs = FLTARR(NV)
; Value of the interest rate and continuous dividend.
r = 0.1
dividend=0.0
; Values of the min and max underlying values modeled.
x_min=0.0
x_max=30.0
; Define parameters for the integration step.
nint = NXGRD-1
n = 3*NXGRD
xgrid = FLTARR(NXGRD)
yb = FLTARR((NTGRD+1)*3*NXGRD)
ybprime = FLTARR((NTGRD+1)*3*NXGRD)
yv = FLTARR((NTGRD+1)*3*NXGRD)
yvprime = FLTARR((NTGRD+1)*3*NXGRD)
fb = FLTARR(NTGRD*NV)
fv = FLTARR(NTGRD*NV)
; Number of left/right boundary conditions.
nlbcd = 3l
nrbcd = 3l
; Structure for the evaluation routines.
usr_data = { , $idope:I32ARR(1), $
rdope:FLTARR(7) $
}
; Define an equally-spaced grid of points for the underlying
; price.
xgrid = INTERPOL([x_min, x_max], NXGRD)
tmp = FINDGEN(NV)
xs = 2.0+(tmp*2.0)
usr_data.rdope(0) = KS1
usr_data.rdope(1) = bet
usr_data.rdope(2) = KS2
usr_data.rdope(3) = x_max
usr_data.rdope(4) = sigma
usr_data.rdope(5) = r
usr_data.rdope(6) = dividend
; Flag the difference in payoff functions
; 1 for the Bet, 2 for the Vertical Spread.
usr_data.idope(0) = 1
ret = FEYNMAN_KAC(nlbcd, nrbcd, $
xgrid, time, "fkcfiv_call", $
"fkbcp_call", yb, ybprime)
usr_data.idope(0) = 2
ret = FEYNMAN_KAC(nlbcd, nrbcd, $
xgrid, time, "fkcfiv_call",$
"fkbcp_call", yv, yvprime)
; Evaluate solutions at vector of points XS(:), at
; each time value prior to expiration.
FOR i=0L, NTGRD-1 DO BEGIN
fb(i*NV:(i*NV)+NV-1) = FEYNMAN_KAC_EVALUATE(xgrid, $
xs, REFORM(yb((i+1),*)))
fv(i*NV:(i*NV)+NV-1) = FEYNMAN_KAC_EVALUATE(xgrid, $
xs, REFORM(yv((i+1),*)))
ENDFOR
PRINT,""
PRINT,"European Option Value for A Bet"
PRINT," and a Vertical Spread, 3 and 6 Months Prior to Expiry"
PRINT," Number of equally spaced spline knots: ", $
STRTRIM(NXGRD,2)
PRINT," Number of unknowns: ",STRTRIM(n,2)
PRINT," Strike=", STRING(KS1,Format="(f5.2)"),$
" Sigma=",STRING(sigma,Format="(f5.2)"),$
" Interest Rate=",STRING(r,Format="(f5.2)")
PRINT," Bet=",STRING(bet,Format="(f5.2)"), $
" Spread Value= ",STRING(KS2,Format="(f5.2)")
PRINT,""
PRINT," Underlying A Bet Vertical Spread
FOR i=0L, NV-1 DO BEGIN
PRINT," ",STRING(xs(i),Format="(f9.4)")," ", $
STRING(fb(i),Format="(f9.4)"), " ",$
STRING(fb(i+NV),Format="(f9.4)")," ",$
STRING(fv(i),Format="(f9.4)"), " ",$
STRING(fv(i+NV),Format="(f9.4)")
ENDFOR
END
; These routines define the coefficients, payoff, boundary
; conditions and forcing term for American and European Options.
FUNCTION fkcfiv_call, x, tx, iflag, value
COMMON f_kac_usr, usr_data
zero=0.0
data = usr_data
data_real = data.rdope
data_int = data.idope
strike_price = data_real(0)
bet = data_real(1)
spread = data_real(2)
sigma = data_real(4)
interest_rate = data_real(5)
dividend = data_real(6)
CASE iflag OF
0:BEGIN
; The payoff function - Use flag passed to decide which.
CASE data_int(0) OF
1:BEGIN
; After reaching the strike price the payoff
; jumps from zero to the bet value.
value = zero
IF (x GT strike_price) THEN value = bet
END
2:BEGIN
; Function is zero up to strike price.
; Then linear between strike price and spread.
; Then has constant value Spread-Strike Price
; after the value Spread.
value = ((x-strike_price)>zero) - (x-spread>zero)
END
ENDCASE
END
-1:BEGIN
; The coefficient derivative d sigma/ dx.
value = sigma
END
1:BEGIN
; The coefficient sigma(x).
value = sigma*x
END
2:BEGIN
; The coefficient mu(x).
value = (interest_rate - dividend)*x
END
3:BEGIN
; The coefficient kappa(x).
value = interest_rate
END
ENDCASE
; Note that there is no time dependence.
iflag = 0
RETURN,1
END
FUNCTION fkbcp_call, nbc, tx, iflag, val
COMMON f_kac_usr, usr_data
data = usr_data
data_int = data.idope
data_real = data.rdope
strike_price = data_real(0)
bet = data_real(1)
spread = data_real(2)
interest_rate = data_real(5)
CASE iflag OF
1:BEGIN
val(*) = 0.0
val(0) = 1.0
val(5) = 1.0
val(10) = 1.0
; Note no time dependence in case (1) for IFLAG.
iflag = 0
END
2:BEGIN
; This is the discount factor using the risk-free
; interest rate.
df = EXP(interest_rate*tx)
; Use flag passed to decide on boundary condition.
CASE data_int(0) OF
1:BEGIN
val(*) = 0.0
val(0) = 1.0
val(3) = bet*df
END
2:BEGIN
val(*) = 0.0
val(0) = 1.0
val(3) = (spread-strike_price)*df
END
ENDCASE
val(5) = 1.0
val(10) = 1.0
END
ENDCASE
RETURN,1
END
Output
European Option Value for A Bet and a Vertical Spread, 3 and 6 Months Prior to Expiry Number of equally spaced spline knots: 61 Number of unknowns: 183 Strike=10.00 Sigma= 0.40 Interest Rate= 0.10 Bet= 2.00 Spread Value= 15.00 Underlying A Bet Vertical Spread 2.0000 0.0000 0.0000 0.0000 0.0000 4.0000 0.0000 0.0014 0.0000 0.0006 6.0000 0.0110 0.0722 0.0039 0.0447 8.0000 0.2691 0.4305 0.1479 0.3831 10.0000 0.9948 0.9781 0.8909 1.1927 12.0000 1.6094 1.4287 2.1911 2.2273 14.0000 1.8655 1.6923 3.4254 3.1552 16.0000 1.9337 1.8177 4.2263 3.8263 18.0000 1.9476 1.8700 4.6264 4.2492 20.0000 1.9501 1.8903 4.7911 4.4921 22.0000 1.9505 1.8979 4.8497 4.6231 24.0000 1.9506 1.9007 4.8684 4.6909Example 4
This example evaluates the price of a convertible bond. Here, convertibility means that the bond may, at any time of the holder’s choosing, be converted to a multiple of the specified asset. Thus a convertible bond with price x returns an amount K at time T unless the owner has converted the bond to vx, v ≥ 1 units of the asset at some time prior to T. This definition, the differential equation and boundary conditions are given in Chapter 18 of Wilmott et al. (1996). Using a constant interest rate and volatility factor, the parameters and boundary conditions are:
1. Bond face value K = {1}, conversion factor v = 1.125
2. Volatility σ = {0.25}
3. Times until expiration = {1/2, 1}
4. Interest rate r = 0.1, dividend D = 0.02
5. xmin = 0, xmax = 4
6. nx = 61, n = 3 × nx = 183
7. Boundary conditions f(0, t) = K exp(–r(T – t)), f(xmax, t) = vxmax
8. Terminal data f(x, T) = max(K, vx)
9. Constraint for bond holder f(x, t) ≥ vx
Note that f(x, t) ≥ vx the error tolerance is set to a pure absolute error of value 10–3. The free boundary constraint f(x, t) ≥ vx is achieved by use of a non-linear forcing term in the user function fkforce_cbond. The terminal conditions are provided with the user function fkinit_cbond.
PRO t_feynman_kac_ex4
COMMON f_kac_usr, usr_data
; Compute value of a Convertible Bond.
NXGRD = 61
NTGRD = 2
NV = 13
; The face value.
KS = 1.0e0
; The sigma or volatility value.
sigma = 0.25e0
; Time values for the options.
time = [ 0.5, 1.0 ]
; Values of the underlying where evaluation are made.
xs = FLTARR(NV)
; Value of the interest rate, continuous dividend and factor.
r = 0.1
dividend=0.02
factor = 1.125
; Values of the min and max underlying values modeled.
x_min = 0.0
x_max = 4.0
; Define parameters for the integration step.
nint = NXGRD-1
n = 3*NXGRD
xgrid = FLTARR(NXGRD)
y = FLTARR((NTGRD+1)*3*NXGRD)
yprime = FLTARR((NTGRD+1)*3*NXGRD)
f = FLTARR((NTGRD+1)*NV)
; Array for user-defined data.
usr_data = FLTARR(8)
; Number of left/right boundary conditions.
nlbcd = 3l
nrbcd = 3l
; Define an equally-spaced grid of points for the
; underlying price.
dx = (x_max-x_min)/(nint)
xgrid = INTERPOL([x_min, x_max], NXGRD)
tmp = FINDGEN(NV)
xs = tmp*0.25
; Pass the data for evaluation.
usr_data(0) = KS
usr_data(1) = x_max
usr_data(2) = sigma
usr_data(3) = r
usr_data(4) = dividend
usr_data(5) = factor
; Use a pure absolute error tolerance for the integration.
atol = 1.0e-3
usr_data(6) = atol
; Compute value of convertible bond.
ret = FEYNMAN_KAC(nlbcd, nrbcd, xgrid, time, $
"fkcfiv_cbond", "fkbcp_cbond", y, yprime, $
Fcn_fkinit="fkinit_cbond", $
Fcn_force="fkforce_cbond", $
ScalarAtolRtol=[1.0e-3, 0.0e0] )
; Evaluate and display solutions at vector of points XS(:),
; at each time value prior to expiration.
FOR i=0L, NTGRD DO BEGIN
f(i*NV:(i*NV)+NV-1) = FEYNMAN_KAC_EVALUATE (xgrid, xs, REFORM(y(i,*)))
ENDFOR
PRINT,"Convertible Bond Value, 0+, 6 and 12 Months Prior"+ $
" to Expiry"
PRINT," Number of equally spaced spline knots: ", $
STRTRIM(NXGRD,2)
PRINT," Number of unknowns:",STRTRIM(n,2)
PRINT," Strike= ",STRING(KS,Format="(f5.2)"), $
" Sigma= ",STRING(sigma,Format="(f5.2)")
PRINT," Interest Rate= ",STRING(r,Format="(f5.2)"), $
" Dividend= ",STRING(dividend,Format="(f5.2)"), $
" Factor= ",STRING(factor,Format="(f6.3)")
PRINT,""
PRINT,"Underlying Bond Value"
FOR i=0L, NV-1 DO BEGIN
PRINT," ",STRING(xs(i),Format="(f8.4)")," ", $
STRING(f(i),Format="(f8.4)")," ", $
STRING(f(i+NV),Format="(f8.4)")," ", $
STRING(f(i+2*NV),Format="(f8.4)")
ENDFOR
END
; These routines define the coefficients, payoff,
; boundary conditions and forcing term.
FUNCTION fkcfiv_cbond, x, tx, iflag, value
COMMON f_kac_usr, usr_data
zero=0.0
data = usr_data
strike_price = data(0)
sigma = data(2)
interest_rate = data(3)
dividend = data(4)
factor = data(5)
CASE iflag OF
0:BEGIN
; The payoff function.
value = (factor * x)>strike_price
END
-1:BEGIN
; The coefficient derivative d sigma/ dx.
value = sigma
END
1:BEGIN
; The coefficient sigma(x).
value = sigma*x
END
2:BEGIN
; The coefficient mu(x).
value = (interest_rate - dividend) * x
END
3:BEGIN
; The coefficient kappa(x).
value = interest_rate
END
ENDCASE
; Note that there is no time dependence.
iflag = 0
RETURN,1
END
FUNCTION fkbcp_cbond, nbc, tx, iflag, val
COMMON f_kac_usr, usr_data
data = usr_data
CASE iflag OF
1:BEGIN
strike_price = data(0)
interest_rate = data(3)
dp = strike_price * EXP(tx*interest_rate)
val(*) = 0.0
val(0) = 1.0
val(3) = dp
val(5) = 1.0
val(10) = 1.0
END
2:BEGIN
x_max = data(1)
factor = data(5)
val(*) = 0.0
val(0) = 1.0
val(3) = factor*x_max
val(5) = 1.0
val(7) = factor
val(10) = 1.0
; Note no time dependence.
iflag = 0
END
ENDCASE
RETURN,1
END
FUNCTION fkforce_cbond, interval, ndeg, nxgrid, y, $
time, width, xlocal, qw, $
u, phi, dphi
COMMON f_kac_usr, usr_data
local=6
yl = FLTARR(local)
bf = FLTARR(local)
zero=0.e0
one=1.0e0
data = usr_data
phi(*) = zero
dphi(*) = zero
yl = y((3*interval)-3+INDGEN(local))
value = data(6)
strike_price = data(0)
interest_rate = data(3)
factor = data(5)
mu = 2.0
; This is the local definition of the forcing term.
; It "forces" the constraint f >= factor*x.
FOR j=1L, local DO BEGIN
FOR l=1L, ndeg DO BEGIN
bf(0) = u((l-1))
bf(1) = u((l-1)+ndeg)
bf(2) = u((l-1)+2*ndeg)
bf(3) = u((l-1)+6*ndeg)
bf(4) = u((l-1)+7*ndeg)
bf(5) = u((l-1)+8*ndeg)
rt = SUM(yl * bf)
rt = value/(rt + value - factor * xlocal(l-1))
phi(j-1) = phi(j-1) + qw(l-1) * bf(j-1) * rt^mu
ENDFOR
ENDFOR
phi = (-phi)*width*factor*strike_price
; This is the local derivative matrix for the forcing term
FOR j=1L, local DO BEGIN
FOR i=1L, local DO BEGIN
FOR l=1L, ndeg DO BEGIN
bf(0) = u((l-1))
bf(1) = u((l-1)+ndeg)
bf(2) = u((l-1)+2*ndeg)
bf(3) = u((l-1)+6*ndeg)
bf(4) = u((l-1)+7*ndeg)
bf(5) = u((l-1)+8*ndeg)
rt = SUM(yl * bf)
rt = one/(rt + value - factor * xlocal(l-1))
dphi(i-1+(j-1)*local) = $
dphi(i-1+(j-1)*local)+qw(l-1) * bf(i-1) * $
bf(j-1) * ((value*rt)^mu) * rt
ENDFOR
ENDFOR
ENDFOR
dphi = dphi *(-mu) * width * factor * strike_price
RETURN,1
END
FUNCTION fkinit_cbond, nxgrid, ntgrid, xgrid, tgrid, $
time, yprime, y, atol, rtol
COMMON f_kac_usr, usr_data
data = usr_data
IF time EQ 0.0 THEN BEGIN
; Set initial data precisely.
FOR i=1L, nxgrid DO BEGIN
IF (xgrid(i-1) * data(5)) LT data(0) THEN BEGIN
y(3*i-3) = data(0)
y(3*i-2) = 0.0
y(3*i-1) = 0.0
ENDIF ELSE BEGIN
y(3*i-3) = xgrid(i-1) * data(5)
y(3*i-2) = data(5)
y(3*i-1) = 0.0
ENDELSE
ENDFOR
ENDIF
RETURN,1
END
Output
Convertible Bond Value, 0+, 6 and 12 Months Prior to Expiry
Number of equally spaced spline knots: 61
Number of unknowns:183
Strike= 1.00 Sigma= 0.25
Interest Rate= 0.10 Dividend= 0.02 Factor= 1.125
Underlying Bond Value
0.0000 1.0000 0.9512 0.9048
0.2500 1.0000 0.9512 0.9049
0.5000 1.0000 0.9513 0.9065
0.7500 1.0000 0.9737 0.9605
1.0000 1.1250 1.1416 1.1464
1.2500 1.4062 1.4117 1.4121
1.5000 1.6875 1.6922 1.6922
1.7500 1.9688 1.9731 1.9731
2.0000 2.2500 2.2540 2.2540
2.2500 2.5312 2.5349 2.5349
2.5000 2.8125 2.8160 2.8160
2.7500 3.0938 3.0970 3.0970
3.0000 3.3750 3.3781 3.3781