NORMALITY Function
Performs a test for normality.
Usage
result = NORMALITY(x)
Input Parameters
x—One-dimensional array containing the observations.
Returned Value
result—The p-value for the Shapiro-Wilk W test or the Lilliefors test for normality. The Shapiro-Wilk test is the default. If the Lilliefors test is used, probabilities less than 0.01 are reported as 0.01, and probabilities greater than 0.10 for the normal distribution are reported as 0.5; otherwise, an approximate probability is computed.
Input Keywords
Double—If present and nonzero, double precision is used.
Ncat—An integer specifying number of cells into which the observations are to be tallied. Keywords Ncat, Df, and Chisq must be used together and indicate that the chi-squared goodness-of-fit test is to be performed.
Output Keywords
Chisq—Specifies a variable into which the chi-square statistic is stored. Keywords Ncat, Df, and Chisq must be used together and indicate that the chi-squared goodness-of-fit test is to be performed.
Df—Specifies a variable into which the degrees of freedom for the test are stored.Keywords Ncat, Df and Chisq must be used together and indicate that the chi-squared goodness-of-fit test is to be performed.
Shapiro_Wilk—Named variable into which the Shapiro-Wilk W statistic is stored. If Shapiro_Wilk is present, then the Shapiro-Wilk W test is performed. Default: Shapiro-Wilk W test is performed
Lilliefors—Named variable into which the maximum absolute difference between the empirical and the theoretical distributions is stored. If Lilliefors is present, then Lilliefors test is performed.
Discussion
Three methods are provided for testing normality: the Chi-Squared test, the Shapiro-Wilk W test, and the Lilliefors test.
Chi-Squared Test
This function computes the chi-squared statistic, its p-value, and the degrees of freedom of the test. Keyword Ncat finds the number of intervals into which the observations are to be divided. The intervals are equiprobable except for the first and last interval which are infinite in length. If more flexibility is desired for the specification of intervals, the same test can be performed with a call to function CHISQTEST using the optional arguments described for that function.
Shapiro-Wilk W Test
D’Agostino and Stevens (1986, p. 406) refer to the Shapiro-Wilk W test as the best omnibus tests of normality. The function is based on the approximations and code given by Royston (1982a, b, c). It can be used in samples as large as 2,000 or as small as 3. In the Shapiro and Wilk test, W is:
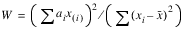
where x(i) is the ith smallest order statistic and:
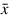
is the sample mean. Royston (1982) gives approximations and tabled values that can be used to compute the coefficients ai, i = 1, ..., n, and obtains the significance level of the W statistic.
Lilliefors Test
This function computes Lilliefors test and its p-values for a normal distribution in which both the mean and variance are estimated. The one-sample, two-sided Kolmogorov-Smirnov statistic D is first computed. The p-values are then computed using an analytic approximation given by Dallal and Wilkinson (1986). Because Dallal and Wilkinson give approximations in the range (0.01, 0.10) if the computed probability of a greater D is less than 0.01, a note is issued and the p-value is set to 0.50. Note that because parameters are estimated, p-values in Lilliefors test are not the same as in the Kolmogorov-Smirnov Test.
Observations should not be tied. If tied observations are found, an informational message is printed. A general reference for the Lilliefors test is Conover (1980). The original reference for the test for normality is Lilliefors (1967).
Example 1
The following example is taken from Conover (1980, pp. 195, 364). The data consists of 50 two-digit numbers taken from a telephone book. The W test fails to reject the null hypothesis of normality at the .05 level of significance. For this example, the data is stored in ASCII file data.dat and read using procedure RMF. The file data.dat contains the following data:
23 36 54 61 73 23 37 54 61 73 24 40 56 62 74
27 42 57 63 75 29 43 57 64 77 31 43 58 65 81
32 44 58 66 87 33 45 58 68 89 33 48 58 68 93
35 48 59 70 97
OPENR, unit, 'data.dat', /Get_Lun
RMF, unit, x, 50, 1
CLOSE, unit
p = NORMALITY(x)
PRINT, 'P-Value = ', p
; PV-WAVE prints: P-Value = 0.230858
Example 2
The following example uses the same data as the previous example. Here, the Shapiro-Wilk W statistic is output.
OPENR, unit, 'data.dat', /Get_Lun
RMF, unit, x, 50, 1
CLOSE, unit
p = NORMALITY(x, Shapiro_Wilk = sw)
PRINT, 'p-Value = ', p
; PV-WAVE prints: p-Value = 0.230858
PRINT, 'Shapiro Wilk W Statistic = ', sw
; PV-WAVE prints: Shapiro Wilk W Statistic = 0.964217
Warning Errors
STAT_ALL_OBS_TIED—All observations in x are tied.
Fatal Errors
STAT_NEED_AT_LEAST_5—All but # elements of x are missing. At least five nonmissing observations are necessary to continue.
STAT_NEG_IN_EXPONENTIAL—In testing the exponential distribution, an invalid element in x is found (x( ) = #). Negative values are not possible in exponential distributions.
STAT_NO_VARIATION_INPUT—There is no variation in the input data. All nonmissing observations are tied.





