CORR1D Function
Compute the discrete correlation of two one-dimensional arrays.
Usage
result = CORR1D(x[, y])
Input Parameters
x—One-dimensional array.
y—(Optional) One-dimensional array.
Returned Value
result—A one-dimensional array containing the discrete convolution of x and x, or x and y if y is supplied.
Input Keywords
Periodic—If present and nonzero, then the input data is periodic
Discussion
The function CORR1D computes the discrete correlation of two sequences x and y. If only one argument is passed, then CORR1D computes the discrete correlation of x and x.
More precisely, let n be the length of x and y. If Periodic is set, then nz = n, otherwise nz is set to the smallest whole number, nz ≥ 2n – 1 , of the form:
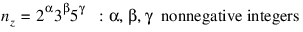
The arrays x and y are then zero-padded to a length nz. Then, we compute:
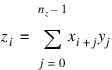
where the index on x is interpreted as a positive number between 0 and nz – 1.
The technique used to compute the zi’s is based on the fact that the (complex discrete) Fourier transform maps correlation into multiplication. Thus, the Fourier transform of z is given by:
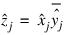
where the following equation is true:
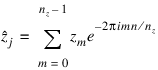
Thus, the technique used here to compute the correlation is to take the discrete Fourier transform of x and the conjugate of the discrete Fourier transform of y, multiply the results together component-wise, and then take the inverse transform of this product. It is very important to make sure that nz is the product of small primes if Periodic is selected. If nz is the product of small primes, then the computational effort will be proportional to nzlog (nz). If Periodic is not set, then a good value is chosen for nz so that the Fourier transforms are efficient and nz ≥ 2n – 1 . This will mean that both vectors may be padded with zeros.
We point out that if x and y are not complex, then no complex transforms of x or y are taken, since a real transforms can simulate the complex transform above. Such a strategy is six times faster and requires less space than when using the complex transform.
Example
In this example, we compute a periodic correlation between two distinct signals x and y. We have 100 equally spaced points on the interval [0, 2π] and f1 (x) = sin (x). We define x and y as follows:
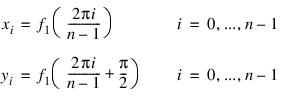
Note that the maximum value of z (the correlation of x with y) occurs at i = 25, which corresponds to the offset.
; Define the signals and compute the norms of the signals.
n = 100
t = 2*!DPI*FINDGEN(n)/(n-1)
x = SIN(t)
y = SIN(t+!dpi/2)
xnorm = NORM(x)
ynorm = NORM(y)
; Compute periodic correlation, and find the largest normalized
; element of the result.
z = CORR1D(x, y, /Periodic)/(xnorm*ynorm)
max_z = (SORT(z))(N_ELEMENTS(z)-1)
PRINT, max_z, z(max_z)
; PV-WAVE prints: 25 1.00





