FRIEDMANS_TEST Function
Performs Friedman’s test for a randomized complete block design.
Usage
result = FRIEDMANS_TEST(y)
Input Parameters
y—Two-dimensional array containing the observations. The first row of y contain the observations on treatments 1, 2, ..., N_ELEMENTS(y(0, *)) in the first block. The second row of y contain the observations in the second block, etc., and so on.
Returned Value
results—The Chi-squared approximation of the asymptotic p-value for Friedman’s two-sided test statistic.
Input Keywords
Double—If present and nonzero, double precision is used.
Fuzz—Nonnegative constant used to determine ties. In the ordered observations, if |y(i) –y(i + 1)| is less than or equal to Fuzz, then y(i) and y(i + 1) are said to be tied. Default: Fuzz = 0.0.
Alpha—Critical level for multiple comparisons. Alpha should be between 0 and 1 exclusive. Default: Alpha = 0.05.
Output Keywords
Stats—Named variable into which the one-dimensional array of length 6 containing the Friedman statistics below is stored. Probabilities reported are computed under the appropriate null hypothesis.
0—Friedman two-sided test statistic.1—Approximate F value for Stats(0).2—Page test statistic for testing the ordered alternative that the median of treatment i is less than or equal to the median of treatment i + 1, with strict inequality holding for some i.3—Asymptotic p-value for Stats(0). Chi-squared approximation.4—Asymptotic p-value for Stats(1). F approximation.5—Asymptotic p-value for Stats(2). Normal approximation.Sum_Rank—Named varaible into which a one-dimensional array of length N_ELEMENTS(x(0, *)) containing the sum of the ranks of each treatment is stored.
Diff—Named variable into which the minimum absolute difference in two elements of Sum_Rank to infer at the Alpha level of significance that the medians of the corresponding treatments are different is stored.
Discussion
Function FRIEDMANS_TEST may be used to test the hypothesis of equality of treatment effects within each block in a randomized block design. No missing values are allowed. Ties are handled by using the average ranks. The test statistic is the nonparametric analogue of an analysis of variance F test statistic.
The test proceeds by first ranking the observations within each block. Let A denote the sum of the squared ranks, i.e., let:
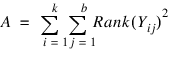
where Rank(Yij) is the rank of the ith observation within the jth block, b is the number of blocks, and k is the number of treatments. Let:
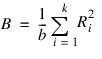
where:
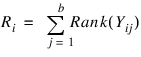
The Friedman test statistic (Stats(0)) is given by:
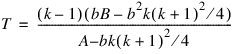
that, under the null hypothesis, has an approximate chi-squared distribution with k – 1 degrees of freedom. The asymptotic probability of obtaining a larger chi-squared random variable is returned in Stats(3).
If the F distribution is used in place of the chi-squared distribution, then the usual oneway analysis of variance F-statistic computed on the ranks is used. This statistic, reported in Stats(1), is given by:
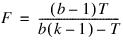
and asymptotically follows an F distribution with (k – 1) and (b –1)(k – 1) degrees of freedom under the null hypothesis. Stats(4) is the asymptotic probability of obtaining a larger F random variable. (If A = B, Stats(0) and Stats(1) are set to machine infinity, and the significance levels are reported as k!/(k!)b, unless this computation would cause underflow, in which case the significance levels are reported as zero.) Iman and Davenport (1980) discuss the relative advantages of the chi-squared and F approximations. In general, the F approximation is considered best.
The Friedman T statistic is related both to the Kendall coefficient of concordance and to the Spearman rank correlation coefficient. See Conover (1980) for a discussion of the relationships.
If, at the α = Alpha level of significance, the Friedman test results in rejection of the null hypothesis, then an asymptotic test that treatments i and j are different is given by: reject H0 if |Ri − Rj| > D, where:
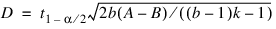
where t has (b – 1)(k – 1) degrees of freedom. Page’s statistic (Stats(2)) is used to test the same null hypothesis as the Friedman test but is sensitive to a monotonic increasing alternative. The Page test statistic is given by
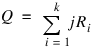
It is largest (and thus most likely to reject) when the Ri are monotonically increasing.
Assumptions
The assumptions in the Friedman test are as follows:
1. The k-vectors of responses within each of the b blocks are mutually independent (i.e., the results within one block have no effect on the results within another block).
2. Within each block, the observations may be ranked.
The hypothesis tested is that each ranking of random variables within each block is equally likely. The alternative is that at least one treatment tends to have larger values than one or more of the other treatments. The Friedman test is a test for the equality of treatment means or medians.
Example
The following example is taken from Bradley (1968), page 127, and tests the hypothesis that 4 drugs have the same effects upon a person’s visual acuity. Five subjects were used.
y = TRANSPOSE([[0.39, 0.55, 0.33, 0.41], $
[0.21, 0.28, 0.19, 0.16], [0.73, 0.69, 0.64, 0.62], $
[0.41, 0.57, 0.28, 0.35], [0.65, 0.57, 0.53, 0.60]])
fuzz = 0.001
p = FRIEDMANS_TEST(y, Fuzz = fuzz, Diff = diff, $
Sum_Rank = sr, Stats = stat)
PM, stat, Title = 'STATS'
; PV-WAVE prints the following:
; STATS
; 8.28000
; 4.92857
; 111.000
; 0.0405658
; 0.0185906
; 0.984954
PM, diff, Title = 'DIFF'
; PV-WAVE prints the following:
; DIFF
; 6.65638
PM, sr, Title = 'Sum_Rank'
; PV-WAVE prints the following:
; Sum_Rank
; 16.0000
; 17.0000
; 7.00000
; 10.0000
The Friedman null hypothesis is rejected at the α = 0.05 while the Page null hypothesis is not. (A Page test with a monotonic decreasing alternative would be rejected, however.) Using Sum_Rank and Diff, one can conclude that treatment 3 is different from treatments 1 and 2, and that treatment 4 is different from treatment 2, all at the α= 0.05 level of significance.
