KW_TEST Function
Performs a Kruskal-Wallis test for identical population medians.
Usage
result = KW_TEST(n, y)
Input Parameters
n—One-dimensional array containing the number of responses for each of the groups.
y—One-dimensional array of length N_ELEMENTS(n) that contains the responses for each of the groups. y must be sorted by group, with the n(0) observations in group 1 coming first, the n(1) observations in group two coming second, and so on.
Returned Value
result—One-dimensional array of length 4 containing the Kruskal-Wallis statistics.
0—Kruskal-Wallis H statistic.1—Asymptotic probability of a larger H under the null hypothesis of identical population medians.2—H corrected for ties.3—Asymptotic probability of a larger H (corrected for ties) under the null hypothesis of identical populationsInput Keywords
Double—If present and nonzero, double precision is used.
Fuzz—Nonnegative constant used to determine ties in y. If (after sorting)
|y(i) – y(i + 1)| is less than or equal to Fuzz, then a tie is counted. Default: Fuzz = 0.0
|y(i) – y(i + 1)| is less than or equal to Fuzz, then a tie is counted. Default: Fuzz = 0.0
Discussion
The function KW_TEST generalizes the Wilcoxon two-sample test computed by WILCOXON Function to more than two populations. It computes a test statistic for testing that the population distribution functions in each of K populations are identical. Under appropriate assumptions, this is a nonparametric analogue of the one-way analysis of variance. Since more than two samples are involved, the alternative is taken as the analogue of the usual analysis of variance alternative, namely that the populations are not identical.
The calculations proceed as follows: All observations are ranked regardless of the population to which they belong. Average ranks are used for tied observations (observations within Fuzz of each other). Missing observations (observations equal to NaN, not a number) are not included in the ranking. Let Ri denote the sum of the ranks in the ith population. The test statistic H is defined as:
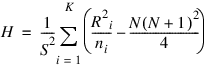
where N is the total of the sample sizes, ni is the number of observations in the ith sample, and S2 is computed as the (bias corrected) sample variance of the Ri.
The null hypothesis is rejected when result(3) (or result(1)) is less than the significance level of the test. If the null hypothesis is rejected, then the procedures given in Conover (1980, page 231) may be used for multiple comparisons. The function KW_TEST computes asymptotic probabilities using the chi-squared distribution when the number of groups is 6 or greater, and a Beta approximation (see Wallace 1959) when the number of groups is 5 or less. Tables yielding exact probabilities in small samples may be obtained from Owen (1962).
Example
The following example is taken from Conover (1980, page 231). The data represents the yields per acre of four different methods for raising corn. Since H = 25.5, the four methods are clearly different. The warning error is always printed when the Beta approximation is used, unless printing for warning errors is turned off.
y = [83.0, 91.0, 94.0, 89.0, 89.0, 96.0, 91.0, 92.0, 90.0, $
91.0, 90.0, 81.0, 83.0, 84.0, 83.0, 88.0, 91.0, 89.0, $
84.0, 101.0, 100.0, 91.0, 93.0, 96.0, 95.0, 94.0, 78.0, $
82.0, 81.0, 77.0, 79.0, 81.0, 80.0, 81.0]
n = [9, 10, 7, 8]
fuzz = 0.001
rlabel = ['H (no ties) =', $
'Prob (no ties) =', $
'H (ties) =', $
'Prob (ties) =']
s = KW_TEST(n, y, Fuzz = fuzz)
; PV-WAVE prints the following:
; % KTRENDS: Warning: <unknown error>
; Error code 30046.
FOR i=0L, 3 DO PM, rlabel(i), s(i), Format = '(A18, F6.2)'
; PV-WAVE prints the following:
; H (no ties) = 25.46
; Prob (no ties) = 0.00
; H (ties) = 25.63
; Prob (ties) = 0.00
