EXACT_NETWORK Function
Computes Fisher exact probabilities and a hybrid approximation of the Fisher exact method for a two-way contingency table using the network algorithm.
Usage
result = EXACT_NETWORK(table)
Input Parameters
table—Two-dimensional array containing the observed counts in the contingency table.
Returned Value
result—The p-value for independence of rows and columns. The p-value represents the probability of a more extreme table where “extreme” is taken in the Neyman-Pearson sense. The p-value is “two-sided”.
Input Keywords
Double—If present and nonzero, double precision is used.
Approx_Params—One-dimensional array of size 3. Approx_Params(0) is the expected value used in the hybrid approximation to Fisher’s exact test algorithm for deciding when to use asymptotic probabilities when computing path lengths. Approx_Params(1) is the percentage of remaining cells that must have estimated expected values greater than Approx_Params(0) before asymptotic probabilities can be used in computing path lengths. Approx_Params(2) is the minimum cell estimated value allowed for asymptotic chi-squared probabilities to be used.
Asymptotic probabilities are used in computing path lengths whenever Approx_Params(1) or more of the cells in the table have estimated expected values of Approx_Params(0) or more, with no cell having expected value less than Approx_Params(2). See the Discussion section for details.
Defaults: Approx_Params(0) = 5.0
Approx_Params(1) = 80.0
Approx_Params(2) = 1.0
note | These defaults correspond to the “Cochran” condition. |
No_Approx—If present and nonzero, the Fisher exact test is used and Approx_Param is ignored.
Wk_Params—One-dimensional array of size 3. The network algorithm requires a large amount of workspace. Some of the workspace requirements are well-defined, while most of the workspace requirements can only be estimated. The estimate is based primarily on table size.
Function EXACT_ENUM allocates a default amount of workspace suitable for small problems. If the algorithm determines that this initial allocation of workspace is inadaquate, the memory is freed, a larger amount of memory allocated (twice as much as the previous allocation), and the network algorithm is re-started. The algorithm allows for up to Wk_Params(2) attempts to complete the algorithm.
Because each attempt requires computer time, it is suggested that Wk_Params(0) and Wk_Params(1) be set to some large numbers (like 1,000 and 30,000) if the problem to be solved is large. It is suggested that Wk_Params(1) be 30 times larger than Wk_Params(0). Although EXACT_ENUM will eventually work its way up to a large enough memory allocation, it is quicker to allocate enough memory initially.
The known (well-defined) workspace requirements are as follows: Define 
equal to the sum of all cell frequencies in the observed table, 
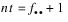, mx = max (n_rows, n_columns), mn = min (n_rows, n_columns), t1 = max (800 + 7mx, (5 + 2mx) (n_rows + n_columns + 1) ), and t2 = max(400 + mx, + 1, n_rows + n_columns + 1) where n_rows = N_ELEMENTS(table(*,0)) and n_columns = N_ELEMENTS(table(0,*)).
equal to the sum of all cell frequencies in the observed table, 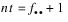, mx = max (n_rows, n_columns), mn = min (n_rows, n_columns), t1 = max (800 + 7mx, (5 + 2mx) (n_rows + n_columns + 1) ), and t2 = max(400 + mx, + 1, n_rows + n_columns + 1) where n_rows = N_ELEMENTS(table(*,0)) and n_columns = N_ELEMENTS(table(0,*)). The following amount of integer workspace is allocated: 3mx + 2mn + t1.
The following amount of real workspace is allocated: nt + t2.
The remainder of workspace that is required must be estimated and allocated based on Wk_Params(0) and Wk_Params(1). The amount of integer workspace allocated is 6n (Wk_Params(0) + Wk_Params(1)). The amount of real workspace allocated is n (6*Wk_Params(0) + 2* Wk_Params(1)). Variable n is the index for the attempt, 1 < n ≤ Wk_Params(2).
Defaults: Wk_Params(0) = 100
Wk_Params(1) = 3000
Wk_Params(2) = 10
Output Keywords
Prob_Table—Named variable into which the probability of the observed table occurring given that the null hypothesis of independent rows and columns is true is stored.
P_Value—Named variable into which the p-value for independence of rows and columns is stored. The p-value represents the probability of a more extreme table where “extreme” is in the Neyman-Pearson sense. The P_Value is “two-sided”. The p-value is also returned in functional form (see Returned Value).
A table is more extreme if its probability (for fixed marginals) is less than or equal to Prob_Table.
Discussion
Function EXACT_NETWORK computes Fisher exact probabilities or a hybrid algorithm approximation to Fisher exact probabilities for an r by c contingency table with fixed row and column marginals (a marginal is the number of counts in a row or column), where r = n_rows and c = n_columns. Let fij denote the count in row i and column j of a table, and let fi and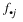 
denote the row and column marginals. Under the hypothesis of independence, the (conditional) probability of the fixed marginals of the observed table is given by:
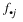denote the row and column marginals. Under the hypothesis of independence, the (conditional) probability of the fixed marginals of the observed table is given by: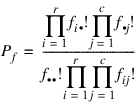
where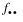 
is the total number of counts in the table. Pf corresponds to output keyword Prob_Table.
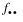is the total number of counts in the table. Pf corresponds to output keyword Prob_Table.A “more extreme” table X is defined in the probablistic sense as more extreme than the observed table if the conditional probability computed for table X (for the same marginal sums) is less than the conditional probability computed for the observed table. The user should note that this definition can be considered “two-sided” in the cell counts.
Example
This example demonstrates various methods of computing chi-squared
p-value with respect to accuracy. As seen in the output of this example, the Fisher exact probability and the usual asymptotic chi-squared probability (generated using function CONTINGENCY) can be different.
p-value with respect to accuracy. As seen in the output of this example, the Fisher exact probability and the usual asymptotic chi-squared probability (generated using function CONTINGENCY) can be different.
PRO print_results, p, p2, p3, p4
PRINT, 'Asymptotic Chi-Squared p-value'
PRINT, 'p-value =', p
PRINT, 'Network Algorithm with Approximation'
PRINT, 'p-value =', p2
PRINT, 'Network Algorithm without Approximation'
PRINT, 'p-value =', p3
PRINT, 'Total Enumeration Method'
PRINT, 'p-value =', p4
END
table = TRANSPOSE([[20, 20, 0, 0, 0], [10, 10, 2, 2, 1], $
[20, 20, 0, 0, 0]])
p = CONTINGENCY(table)
p2 = EXACT_NETWORK(table)
p3 = EXACT_NETWORK(table, /No_Approx)
p4 = EXACT_ENUM(table)
print_results, p, p2, p3, p4
This results in the following output:
% CONTINGENCY: Warning: STAT_EXP_VALUES_TOO_SMALL
Some expected values are less than 1. Some asymptotic
p-values may not be good.
Asymptotic Chi-Squared p-value
p-value = 0.0322604
Network Algorithm with Approximation
p-value = 0.0601165
Network Algorithm without Approximation
p-value = 0.0598085
Total Enumeration Method
p-value = 0.0597294
Warning Errors
STAT_HASH_TABLE_ERROR_2—The value “ldkey” = # is too small. “ldkey” is calculated as Wk_Params(0)*pow(10, N_Attempts−1) ending this execution attempt.
STAT_HASH_TABLE_ERROR_3—The value “ldstp” = # is too small. “ldstp” is calculated as Wk_Params(1)*pow(10, N_Attempts−1) ending this execution attempt.
Fatal Errors
STAT_HASH_TABLE_ERROR_1—The hash table key cannot be computed because the largest key is larger than the largest representable integer. The algorithm cannot proceed.
