EXACT_ENUM Function
Computes exact probabilities in a two-way contingency table using the total enumeration method.
Usage
result = EXACT_ENUM(table)
Input Parameters
table—Two-dimensional array containing the observed counts in the contingency table.
Returned Value
result—The p-value for independence of rows and columns. The p-value represents the probability of a more extreme table where “extreme” is taken in the Neyman-Pearson sense. The p-value is “two-sided”.
Input Keywords
Double—If present and nonzero, double precision is used.
Output Keywords
Prob_Table—Named variable into which the probability of the observed table occurring, given that the null hypothesis of independent rows and columns is true, is stored.
P_Value—Named variable into which the p-value for independence of rows and columns is stored. The p-value represents the probability of a more extreme table where “extreme” is taken in the Neyman-Pearson sense. The p-value is “two-sided”.
The p-value is also returned in functional form (see Returned Value).
A table is more extreme if its probability (for fixed marginals) is less than or equal to Prob_Table.
Error_Chk—Named variable into which the sum of the probabilities of all tables with the same marginal totals is stored. Keyword Error_Chk should have a value of 1.0. Deviation from 1.0 indicates numerical error.
Discussion
Function EXACT_ENUM computes exact probabilities for an r by c contingency table for fixed row and column marginals (a marginal is the number of counts in a row or column), where r = N_ELEMENTS(table(*,0)) and c = N_ELEMENTS(table(0,*)). Let fij denote the count in row i and column j of a table, and let 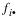 and
and 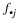 denote the row and column marginals. Under the hypothesis of independence, the (conditional) probability of the fixed marginals of the observed table is given by:
denote the row and column marginals. Under the hypothesis of independence, the (conditional) probability of the fixed marginals of the observed table is given by:
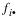 and
and 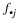 denote the row and column marginals. Under the hypothesis of independence, the (conditional) probability of the fixed marginals of the observed table is given by:
denote the row and column marginals. Under the hypothesis of independence, the (conditional) probability of the fixed marginals of the observed table is given by: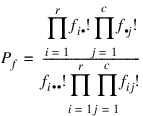
where 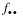 is the total number of counts in the table. Pf corresponds to output keyword Prob_Table.
is the total number of counts in the table. Pf corresponds to output keyword Prob_Table.
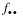 is the total number of counts in the table. Pf corresponds to output keyword Prob_Table.
is the total number of counts in the table. Pf corresponds to output keyword Prob_Table.A more extreme table X is defined in the probablistic sense as more extreme than the observed table if the conditional probability computed for table X (for the same marginal sums) is less than the conditional probability computed for the observed table. The user should note that this definition can be considered “two-sided” in the cell counts.
Because EXACT_ENUM uses total enumeration in computing the probability of a more extreme table, the amount of computer time required increases very rapidly with the size of the table. Tables with a large total count 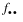 or a large value of r by c should not be analyzed using EXACT_ENUM. In such cases, try using EXACT_NETWORK.
or a large value of r by c should not be analyzed using EXACT_ENUM. In such cases, try using EXACT_NETWORK.
 or a large value of r by c should not be analyzed using EXACT_ENUM. In such cases, try using EXACT_NETWORK.
or a large value of r by c should not be analyzed using EXACT_ENUM. In such cases, try using EXACT_NETWORK.Example
In this example, the exact conditional probability for the 2 by 2 contingency table is computed as follows:
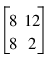
table = [[8, 8], [12, 2]]
p = EXACT_ENUM(table, P_Value=pv, Prob_Table=pt, Error_Chk=ec)
PRINT, 'p-value =', p ; PV-WAVE prints: p-value = 0.0576712





