FCN_DERIV Function
Computes the first, second, or third derivative of a user-supplied function.
Usage
result = FCN_DERIV(f, x)
Input Parameters
f—Scalar string specifying a user-supplied function whose derivative at x will be computed.
x—Point at which the derivative will be evaluated.
Returned Value
result—An estimate of the first, second or third derivative of f at x. If no value can be computed, NaN is returned.
Input Keywords
Double—If present and nonzero, double precision is used.
Order—The order of the desired derivative (1, 2, or 3). Default: Order = 1
Stepsize—Beginning value used to compute the size of the interval for approximating the derivative. Stepsize must be chosen small enough that f is defined and reasonably smooth in the interval (x – 4.0*Stepsize, x + 4.0*Stepsize), yet large enough to avoid roundoff problems. Default: Stepsize = 0.01
Tolerance—The relative error desired in the derivative estimate. Convergence is assumed when (2/3) |d2 – d1| < Tolerance, for two successive derivative estimates, d1 and d2. Default: Tolerance = 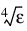 where ε is machine epsilon.
where ε is machine epsilon.
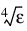 where ε is machine epsilon.
where ε is machine epsilon.Discussion
The function FCN_DERIV produces an estimate to the first, second, or third derivative of a function. The estimate originates from first computing a spline interpolant to the input function using values within the interval (x – 4.0*Stepsize, x + 4.0*Stepsize), then differentiating the spline at x.
Example 1
This example obtains the approximate first derivative of the function f(x) = –2sin(3x/2) at the point x = 2.
FUNCTION fcn, x
f = -2*SIN(1.5*x)
RETURN, f
END
deriv1 = FCN_DERIV('fcn', 2.0)PRINT, 'f''(x) = ', deriv1
; PV-WAVE prints: f'(x) = 2.97008
Example 2
This example obtains the approximate first, second, and third derivative of the function f(x) = –2sin(3x/2) at the point x = 2.
FUNCTION fcn, x
f = -2*SIN(1.5*x)
RETURN, f
END
deriv1 = FCN_DERIV('fcn', 2.0, /Double)deriv2 = FCN_DERIV('fcn', 2.0, ORDER = 2, /Double)deriv3 = FCN_DERIV('fcn', 2.0, ORDER = 3, /Double)PRINT, 'f''(x) = ', deriv1, ', error =', $
ABS(deriv1 + 3.0*COS(1.5*2.0))
; PV-WAVE prints: f'(x) = 2.9699775, error = 1.1094893e-07
PRINT, 'f''''(x) = ', deriv2, ', error =', $
ABS(deriv2 - 4.5*SIN(1.5*2.0))
; PV-WAVE prints: f''(x) = 0.63504004, error = 5.1086361e-08
PRINT, 'f''''''(x) = ', deriv3, ', error =', $
ABS(deriv3 - 6.75*COS(1.5*2.0))
; PV-WAVE prints: f'''(x) = -6.6824494, error = 1.1606068e-08





