GQUAD Procedure
Computes a Gauss, Gauss-Radau, or Gauss-Lobatto quadrature rule with various classical weight functions.
Usage
GQUAD, n, weights, points
Input Parameters
n—Number of quadrature points.
Output Parameters
weights—Named variable into which an array of length n containing the quadrature weights is stored.
points—Named variable into which an array of length n containing quadrature points is stored. The default action of this routine is to produce the Gauss Legendre points and weights.
Input Keywords
Double—If present and nonzero, double precision is used.
Cheby_First—Computes the Gauss points and weights using the weight function:
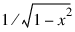
on the interval (–1, 1).
Cheby_Second—Computes the Gauss points and weights using the weight function:
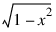
on the interval (–1, 1).
Hermite—Computes the Gauss points and weights using the weight function exp (–x2) on the interval (–infinity, infinity ).
Cosh—Computes the Gauss points and weights using the weight function
1/cosh (x) on the interval (–infinity, infinity ).
1/cosh (x) on the interval (–infinity, infinity ).
Jacobi—Specifies an array of length 2 containing the parameters α and β to be used in the weight function 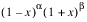 . If this keyword is present, computes the Gauss points and weights using the weight function
. If this keyword is present, computes the Gauss points and weights using the weight function 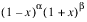 on the interval (–1, 1).
on the interval (–1, 1).
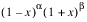 . If this keyword is present, computes the Gauss points and weights using the weight function
. If this keyword is present, computes the Gauss points and weights using the weight function 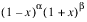 on the interval (–1, 1).
on the interval (–1, 1).Laguerre—Specifies the parameter α to be used in the weight function exp(–x) xα. If this keyword is present, computes the Gauss points and weights using the weight function exp (–x) xα on the interval (0, infinity).
Fixed_Points—Specifies an array of fixed points. The length of the array can be a maximum of 2.
There are two distinct actions taken depending on the length of this array. If Fixed_Points specifies an array of length 1 (a scalar), the procedure computes the Gauss-Radau points and weights using the specified weight function and the fixed point. This formula integrates polynomials of degree less than 2N–1 exactly. If Fixed_Points specifies an array of length 2, the procedure computes the Gauss-Lobatto points and weights using the specified weight function and the fixed points. This formula integrates polynomials of degree less than 2N–2 exactly.
Discussion
Procedure GQUAD produces the points and weights for the Gauss, Gauss-Radau, or Gauss-Lobatto quadrature formulas for some of the most popular weights. The default weight is the weight function identically equal to 1 on the interval (–1, 1). In fact, it is slightly more general than this suggests because the extra one or two points that can be specified do not have to lie at the endpoints of the interval. This procedure is a modification of the subroutine GAUSSQUADRULE (Golub and Welsch 1969).
In the default case, the procedure returns points in x = points and weights in w = weights so that:
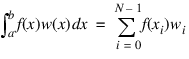
for all functions f that are polynomials of degree less than 2N.
If Fixed_Points is specified, then one or two of the above xi is equal to the values specified by Fixed_Points. In general, the accuracy of the above quadrature formula degrades when n increases. The quadrature rule integrates all functions f that are polynomials of degree less than 2N – F, where F is the number of fixed points.
Example
The three-point Gauss Legendre quadrature points and weights are computed, then used to approximate the integrals as follows:
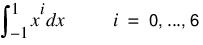
Notice that the integrals are exact for the first six monomials, but the last approximation is in error. In general, the Gauss rules with k-points integrate polynomials with degree less than 2k exactly.
; Call GQUAD to get the weights and points.
GQUAD, 3, weights, points
; Define an array to hold the errors.
error = FLTARR(7)
; Compute the errors for seven monomials.
FOR i=0L, 6 DO error(i) = $
(TOTAL(weights*(points^i))-(1-(i MOD 2))*2./(i+1))
; Output the results.
PM, 'Error:', error
; On 32-bit Windows, this produces the following output:
; Error:
; -2.38419e-007
; 3.01335e-007
; 0.000000
; 1.49012e-007
; -2.98023e-008
; 1.04308e-007
; -0.0457143





