INTFCN_QMC Function
Integrates a function on a hyper-rectangle using a quasi-Monte Carlo method.
Usage
result = INTFCN_QMC(f, a, b)
Input Parameters
f—Scalar string specifying the user-supplied function to be integrated. Function f accepts as input an array of data points at which the function is to be evaluated and returns the scalar value of the function.
a—One-dimensional array containing the lower limits of integration.
b—One-dimensional array containing the upper limits of integration.
Returned Value
The value of:
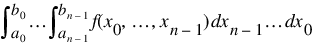
is returned. If no value can be computed, then NaN is returned.
Input Keywords
Err_Abs—Absolute accuracy desired. Default: Err_Abs = 1.E–4.
Err_Rel—Relative accuracy desired. Default: Err_rel = 1.E–4.
Max_Evals—Number of evaluations allowed. Default: No limit
Base—The value of BASE used to compute the Faure sequence.
Skip—The value of SKIP used to compute the Faure sequence.
Double—If present and nonzero, double precision is used.
Output Keywords
Err_est—Named variable into which an estimate of the absolute value of the error is stored.
Discussion
Integration of functions over hypercubes by direct methods, such as INTFCNHYPER, is practical only for low dimensional hypercubes, because the amount of work required increases exponentially as the dimension increases.
An alternative to direct methods is Monte Carlo, in which the integral is evaluated as the value of the function averaged over a sequence of randomly chosen points. Under mild assumptions on the function, this method will converge like 1/n1/2, where n is the number of points at which the function is evaluated.
It is possible to improve on the performance of Monte Carlo by carefully choosing the points at which the function is to be evaluated. Randomly distributed points tend to be non-uniformly distributed. The alternative to at sequence of random points is a low-discrepancy sequence. A low-discrepancy sequence is one that is highly uniform.
This function is based on the low-discrepancy Faure sequence, as computed by FAURE_NEXT_PT.
Example
FUNCTION F, x
S = 0.0
sign = -1.0
FOR i=0L, N_ELEMENTS(x)-1 DO BEGIN
prod = 1.0
FOR j=0L, i DO BEGIN
prod = prod*x(j)
END
S = S + sign*prod
sign = -sign
END
RETURN, s
END
ndim = 10
a = FLTARR(ndim)
a(*) = 0
b = FLTARR(ndim)
b(*) = 1
result = INTFCN_QMC( 'f', a, b)
PM, result ; PV-WAVE prints: -0.333010





