SPINTEG Function
Computes the integral of a one- or two-dimensional spline.
Usage
result = SPINTEG(a, b, spline)
result = SPINTEG(a, b, c, d, spline)
Input Parameters
If integration of a one-dimensional spline is desired, then arguments a, b, and spline are required. If integration of a two-dimensional spline is desired, then a, b, c, d, and spline are required.
a—Right endpoint of integration.
b—Left endpoint of integration.
c—Right endpoint of integration for the second variable of the tensor-product spline. This argument should only be used if spline is a two-dimensional, tensor-product spline.
d—Left endpoint of integration for the second variable of the tensor-product spline. This argument should only be used if spline is a two-dimensional, tensor-product spline.
spline—Structure that represents the spline to be integrated.
Returned Value
result—If spline is a one-dimensional spline, then the returned value is the integral from a to b of spline. If spline is a two-dimensional, tensor-product spline, then the returned value is the value of the integral of spline over the rectangle [a, b] × [c, d]. If no value can be computed, NaN (Not a Number) is returned.
Discussion
Function SPINTEG can be used to integrate splines of the following type:
Piecewise polynomials returned by CSINTERP, CSSHAPE, and CSSMOOTH.One-dimensional B-splines returned by BSINTERP, BSLSQ, and CONLSQ.Two-dimensional, tensor-product B-splines returned from BSINTERP and BSLSQ.If s = spline is a one-dimensional piecewise polynomial or B-spline, then SPINTEG computes:
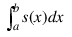
If spline is a one-dimensional B-spline, then this function uses identity (22) of de Boor (1978, p. 115).
If s = spline is a two-dimensional, tensor-product spline, then the arguments c and d are required, and SPINTEG computes:
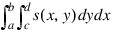
This function uses the (univariate integration) identity (22) of de Boor (1978, p. 151):
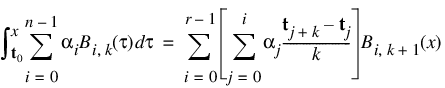
where t0 ≤ x ≤ tr. It assumes (for all knot sequences) that the first and last k knots are stacked; that is, t0 = ... = tk – 1 and tn = ... = tn + k – 1, where k is the order of the spline in the x or y direction.
Example
In this example, a cubic spline interpolant to function values is computed. The values of the integral of this spline are then compared with the exact integral values. Since the default settings are being used, the interpolant is determined by the not-a-knot condition (de Boor 1978).
; Generate the data.
n = 21
x = FINDGEN(n)/(n - 1)
f = SIN(15 * x)
; Compute the interpolant.
pp = CSINTERP(x, f)
; Define an array to hold some results to be output later.
results = FLTARR(22, 4)
; Loop over different limits of integration and compare the
; results with the true answer.
FOR i=n/2, 3 * n/2 DO BEGIN $
x2 = i/FLOAT(2 * n - 2) & $
y = SPINTEG(0, x2, pp) & $
results(i - n/2, *) = & $
[x2, (1 - COS(15 * x2))/15, y, & $
ABS((1 - COS(15 * x2))/15 - y)] & $
ENDFOR
; Output the results.
PM, results, Format = '(4f12.4)', $
Title = ' X True Approx Error'
; PV-WAVE prints the following:
; X True Approx Error
; 0.2500 0.1214 0.1215 0.0001
; 0.2750 0.1036 0.1037 0.0001
; 0.3000 0.0807 0.0808 0.0001
; 0.3250 0.0559 0.0560 0.0001
; 0.3500 0.0325 0.0327 0.0001
; 0.3750 0.0139 0.0141 0.0002
; 0.4000 0.0027 0.0028 0.0002
; 0.4250 0.0003 0.0004 0.0002
; 0.4500 0.0071 0.0073 0.0002
; 0.4750 0.0223 0.0224 0.0001
; 0.5000 0.0436 0.0437 0.0001
; 0.5250 0.0681 0.0682 0.0001
; 0.5500 0.0924 0.0925 0.0001
; 0.5750 0.1131 0.1132 0.0001
; 0.6000 0.1274 0.1275 0.0001
; 0.6250 0.1333 0.1333 0.0001
; 0.6500 0.1298 0.1299 0.0001
; 0.6750 0.1176 0.1177 0.0001
; 0.7000 0.0984 0.0985 0.0001
; 0.7250 0.0747 0.0748 0.0001
; 0.7500 0.0499 0.0500 0.0001
; 0.7750 0.0274 0.0276 0.0001
Warning Errors
MATH_SPLINE_LEFT_ENDPT—Left endpoint of x integration is not within the knot sequence. Integration occurs only from tOrder – 1 to b.
MATH_SPLINE_RIGHT_ENDPT—Right endpoint of x integration is not within the knot sequence. Integration occurs only from tOrder – 1 to a.
MATH_SPLINE_LEFT_ENDPT_1—Left endpoint of x integration is not within the knot sequence. Integration occurs only from b to tSpline_Space_Dim – 1.
MATH_SPLINE_RIGHT_ENDPT_1—Right endpoint of x integration is not within the knot sequence. Integration occurs only from a to tSpline_Space_Dim – 1.
MATH_SPLINE_LEFT_ENDPT_2—Left endpoint of y integration is not within the knot sequence. Integration occurs only from tOrder – 1 to d.
MATH_SPLINE_RIGHT_ENDPT_2—Right endpoint of y integration is not within the knot sequence. Integration occurs only from tOrder – 1 to c.
MATH_SPLINE_LEFT_ENDPT_3—Left endpoint of y integration is not within the knot sequence. Integration occurs only from d to tSpline_Space_Dim – 1.
MATH_SPLINE_RIGHT_ENDPT_3—Right endpoint of y integration is not within the knot sequence. Integration occurs only from c to tSpline_Space_Dim – 1.
Fatal Errors
MATH_KNOT_MULTIPLICITY—Multiplicity of the knots cannot exceed the order of the spline.
MATH_KNOT_NOT_INCREASING—Knots must be nondecreasing.
