NONLINOPT Function
Fits data to a nonlinear model (possibly with linear constraints) using the successive quadratic programming algorithm (applied to the sum of squared errors, SSE = Σ(yi − f(xi; θ))2) and either a finite difference gradient or a user-supplied gradient.
Usage
result = NONLINOPT(f, n_parameters, x, y)
Input Parameters
f—Scalar string specifying a user-supplied function that defines the nonlinear regression problem at a given point. Function f has the following parameters:
xi—One-dimensional array of length n_independent at which point the function is evaluated.theta—One-dimensional array of length n_parameters containing the current values of the regression coefficients.Function f returns a predicted value at the point xi. In the following,
f(xi; θ), or just fi, denotes the value of this function at the point xi, for a given value of θ. (Both xi and θ are arrays.).
f(xi; θ), or just fi, denotes the value of this function at the point xi, for a given value of θ. (Both xi and θ are arrays.).
n_parameters—Number of parameters to be estimated.
x—Two-dimensional array of size n_observations by n_independent containing the matrix of independent (explanatory) variables where n_observations is the number of observations and n_independent is the number of independent variables.
y—One-dimensional array of length n_observations containing the dependent (response) variable.
Returned Value
result—One-dimensional array of length n_parameters containing solution:
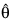
for the nonlinear regression coefficients.
Input Keywords
Double—If present and nonzero, double precision is used.
Theta_Guess—One-dimensional array with n_parameters components containing an initial guess. Default: Theta_Guess(*) = 0
Jacobian—Scalar string specifying a user-supplied function to compute the ith row of the Jacobian. The function specified by Jacobian has the following parameters:
Xi—One-dimensional array containing the n_independent data values corresponding to the ith row. (Input)Theta—One-dimensional array of length n_parameters containing the regression coefficients for which the Jacobian is evaluated. (Input)The return value of this function is a one-dimensional array containing the computed n_parameters row of the Jacobian for observation i at Theta. Note that each derivative f(xi)/θ should be returned in element (j – 1) of the returned array for j = 1, 2, ..., n_parameters. Further note that in order to maintain consistency with the other nonlinear solver, NONLINREGRESS, the Jacobian values must be specified as the negative of the calculated derivatives.
Xlb—One-dimensional array of length n_parameters containing the lower bounds on the parameters; choose a very large negative value if a component should be unbounded below or set Xlb(i) = Xub(i) to freeze the ith variable. Default: All parameters are bounded below by –106.
Xub—One-dimensional array of length n_parameters containing the upper bounds on the parameters; choose a very large value if a component should be unbounded above or set Xlb(i) = Xub(i) to freeze the ith variable. Default: All parameters are bounded above by 106.
A_Matrix—Two-dimensional array of size n_constraints by n_parameters containing the equality constraint gradients in the first Meq rows, followed by the inequality constraint gradients. Here n_constraints is the total number of linear constraints (excluding simple bounds). A_Matrix and B must be used together. Default: There are no default linear constraints.
B—One-dimensional array of length n_constraints containing the right-hand sides of the linear constraints. Keywords A_Matrix and B must be used together. Default: There are no default linear constraints.
A_Matrix and B are the linear constraints, specifically, the constraints on θ are:
ai1 θ 1 + ... + aij θj = bi
for i = 1, n_equality and j = 1, n_parameter, and:
ak1 θ 1 + ... + akj θj ≤ bk
for k = n_equality + 1, n_constraints and j = 1, n_parameter.
Meq—Number of the A_Matrix constraints which are equality constraints; the remaining (n_constraints – Meq) constraints are inequality constraints. Default: Meq = 0.
Frequencies—One-dimensional array of length n_observations containing the frequency for each observation. Default: Frequencies(*) = 1
Weights—One-dimensional array of length n_observations containing the weight for each observation. Default: Weights(*) = 1
Acc—The nonnegative tolerance on the first order conditions at the calculated solution.
Max_Sse_Evals—The maximum number of SSE evaluations allowed. Default: Max_Sse_Eval = 400
Output Keywords
Stop_Info—Named variable into which one of the following integer values to indicate the reason for leaving the routine is stored:
Stop_info | Reason for leaving routine |
|---|---|
1 | θ is feasible, and the condition that depends on Acc is satisfied. |
2 | θ is feasible, and rounding errors are preventing further progress. |
3 | θ is feasible, but sse fails to decrease although a decrease is predicted by the current gradient vector. |
4 | The calculation cannot begin because A_Matrix contains fewer than n_constraints constraints or because the lower bound on a variable is greater than the upper bound. |
5 | The equality constraints are inconsistent. These constraints include any components of 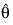 that are frozen by setting Xlb(i) equal to Xub(i). |
6 | The equality constraints and the bound on the variables are found to be inconsistent. |
7 | There is no possible 1 that satisfies all of the constraints. |
8 | Maximum number of sse evaluations (Max_Sse_Eval) is exceeded. |
9 | θ is determined by the equality constraints. |
Num_Active—Named variable into which the final number of active constraints is stored.
Active_Const—Named variable into which a one-dimensional array of length Num_Active containing the indices of the final active constraints is stored.
Lagrange_Mult—Named variable into which a one-dimensional array of length Num_Active containing the Lagrange multiplier estimates of the final active constraints is stored.
Predicted—Named variable into which a one-dimensional array of length n_observations containing the predicted values at the approximate solution is stored.
Residual—Named variable into which a one-dimensional array of length n_observations containing the residuals at the approximate solution is stored.
Sse—Named variable into which the residual sum of squares is stored.
Discussion
Function NONLINOPT is based on M.J.D. Powell’s TOLMIN, which solves linearly constrained optimization problems, i.e., problems of the form min f(q),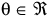 
, subject to:
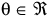, subject to:A1θ = b1
A ≤ b2
θ I ≤ θ ≤ θu
given the vectors b1, b2, θI, and θu and the matrices A1 and A2.
The algorithm starts by checking the equality constraints for inconsistency and redundancy. If the equality constraints are consistent, the method will revise θ0, the initial guess provided by the user, to satisfy:
A1 θ = b1
Next, θ0 is adjusted to satisfy the simple bounds and inequality constraints. This is done by solving a sequence of quadratic programming subproblems to minimize the sum of the constraint or bound violations.
Now, for each iteration with a feasible θk, let Jk be the set of indices of inequality constraints that have small residuals. Here, the simple bounds are treated as inequality constraints. Let Ik be the set of indices of active constraints. The following quadratic programming problem:
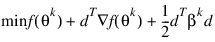
subject to:
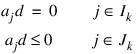
is solved to get (dk, λk) where aj is a row vector representing either a constraint in A1 or A2 or a bound constraint on θ. In the latter case, the aj = ei for the bound constraint θi ≤ (θu)i and aj = ei for the constraint θi ≤ (θl )i. Here, ei is a vector with a 1 as the ith component, and zeroes elsewhere. λk are the Lagrange multipliers, and Bk is a positive definite approximation to the second derivative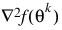 
.
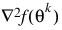. After the search direction dk is obtained, a line search is performed to locate a better point. The new point θk+1 = θk + αkdk has to satisfy the conditions:
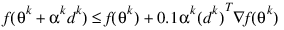
and:
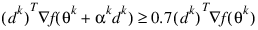
The main idea in forming the set Jk is that, if any of the inequality constraints restricts the step-length αk, then its index is not in Jk. Therefore, small steps are likely to be avoided.
Finally, the second derivative approximation, Bk, is updated by the BFGS formula, if the condition:
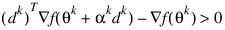
holds. Let θk ← θk+1, and start another iteration.
The iteration repeats until the stopping criterion:
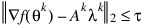
is satisfied; here, τ is a user-supplied tolerance. For more details, see Powell (1988, 1989).
Since a finite-difference method is used to estimate the gradient, for some single precision calculations. An inaccurate estimate of the gradient may cause the algorithm to terminate at a noncritical point. In such cases, high precision arithmetic is recommended. Also, whenever the exact gradient can be easily provided, the gradient should be passed to NONLINOPT using the optional keyword Jacobian.
Example 1
In this example, a data set is fitted to the nonlinear model function:
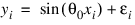
FUNCTION fcn, x, theta
res = SIN(theta(0)*x(0))
RETURN, res
END
x = [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
y = [0.05, 0.21, 0.67, 0.72, 0.98, 0.94, 1.00, 0.73, 0.44, $
0.36, 0.02]
n_parameters = 1
theta_hat = NONLINOPT('fcn', n_parameters, x, y); % NONLINOPT: Note: STAT_NOTE_3
; 'theta' is feasible but the objective function fails to
; decrease. Using double precision may help.
PRINT, 'Theta Hat = ', theta_hat
; PV-WAVE prints: Theta Hat = 3.16143
Example 2
Draper and Smith (1981, p. 475) state a problem due to Smith and Dubey. [H. Smith and S. D. Dubey (1964), “Some reliability problems in the chemical industry", Industrial Quality Control, 21 (2), 1964, pp. 641470] A certain product must have 50% available chlorine at the time of manufacture. When it reaches the customer 8 weeks later, the level of available chlorine has dropped to 49%. It was known that the level should stabilize at about 30%. To predict how long the chemical would last at the customer site, samples were analyzed at different times. It was postulated that the following nonlinear model should fit the data:
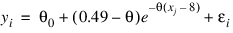
Since the chlorine level will stabilize at about 30%, the initial guess for theta1 is 0.30. Using the last data point (x = 42, y = 0.39) and θ0 = 0.30 and the above nonlinear equation, an estimate for θ1 of 0.02 is obtained.
The constraints that θ0 ≥ 0 and θ1 ≥ 0 are also imposed. These are equivalent to requiring that the level of available chlorine always be positive and never increase with time.
The Jacobian of the nonlinear model equation is also used.
FUNCTION fcn, x, theta
res = theta(0) + (0.49-theta(0))* exp(-theta(1)*(x(0) - 8.0))
RETURN, res
END
FUNCTION jacobian, x, theta
fjac = theta
fjac(*) = 0
fjac(0) = -1.0 + exp(-theta(1)*(x(0) - 8.0));
fjac(1) = (0.49 - theta(0))*(x(0) - 8.0) * $
exp(-theta(1)*(x(0) - 8.0));
RETURN, fjac
END
x = [8.0, 8.0, 10.0, 10.0, 10.0, 10.0, 12.0, 12.0, 12.0, $
12.0, 14.0, 14.0, 14.0, 16.0, 16.0, 16.0, 18.0, 18.0, $
20.0, 20.0, 20.0, 22.0, 22.0, 22.0, 24.0, 24.0, 24.0, $
26.0, 26.0, 26.0, 28.0, 28.0, 30.0, 30.0, 30.0, 32.0, $
32.0, 34.0, 36.0, 36.0, 38.0, 38.0, 40.0, 42.0]
y = [0.49, 0.49, 0.48, 0.47, 0.48, 0.47, 0.46, 0.46, 0.45, $
0.43, 0.45, 0.43, 0.43, 0.44, 0.43, 0.43, 0.46, 0.45, $
0.42, 0.42, 0.43, 0.41, 0.41, 0.40, 0.42, 0.40, 0.40, $
0.41, 0.40, 0.41, 0.41, 0.40, 0.40, 0.40, 0.38, 0.41, $
0.40, 0.40, 0.41, 0.38, 0.40, 0.40, 0.39, 0.39]
theta_guess = [0.3, 0.02]
xlb = [0.0, 0.0]
n_parameters = 2
theta_hat = NONLINOPT('fcn', n_parameters, x, y, $Theta_Guess = theta_guess, Xlb = xlb, $
Jacobian = 'jacobian', Sse = sse)
; % NONLINOPT: Note: STAT_NOTE_3
; 'theta' is feasible but the objective function fails to
; decrease. Using double precision may help.
PRINT, 'Theta Hat =', theta_hat
; PV-WAVE prints: Theta Hat = 0.390143 0.101631
PRINT, 'Residual Sum of Squares =', sse
; PV-WAVE prints: Residual Sum of Squares = 0.00500168
Fatal Errors
STAT_BAD_CONSTRAINTS_1—The equality constraints are inconsistent.
STAT_BAD_CONSTRAINTS_2—The equality constraints and the bounds on the variables are found to be inconsistent.
STAT_BAD_CONSTRAINTS_3—No vector “theta” satisfies all of the constraints. Specifically, the current active constraints prevent any change in “theta” that reduces the sum of constraint violations.
STAT_BAD_CONSTRAINTS_4—The variables are determined by the equality constraints.
STAT_TOO_MANY_ITERATIONS_1—Number of function evaluations exceeded “maxfcn” = #.
