SP_MVMUL Function
Computes a matrix-vector product involving sparse matrix and a dense vector.
Usage
Matrix stored in coordinate format:
result = SP_MVMUL(n_rows, n_cols, a, x)
result = SP_MVMUL(n_rows, n_cols, a, x)
Matrix stored in Band format:
result = SP_MVMUL(n_rows, n_cols, nlca, nuca, a, x)
result = SP_MVMUL(n_rows, n_cols, nlca, nuca, a, x)
Input Parameters
nrows—Number of rows in the matrix a.
ncols—Number of columns in the matrix a.
nlca—Number of lower codiagonals in a. nuca should be used if a is stored in band format.
nuca—Number of upper codiagonals in a. nlca should be used if a is stored in band format.
a—If in coordinate format, a sparse matrix stored as an array of structures. If banded, an array of size (nlca + nuca + 1) × nrows containing the nrows × ncols banded coefficient matrix in band storage mode. If banded, and the keyword Symmetric is set, an array of size (nlca + 1) × nrows containing the nrows × ncols banded coefficient matrix in band symmetric storage mode A(i,j). See the chapter introduction for a description of band storage mode.
x—One-dimensional matrix containing the vector to be multiplied by a.
Returned Value
result—A one-dimensional array containing the product Ax = b.
Input Keywords
Symmetric—If present and nonzero, then a is stored in symmetric mode. If A is in coordinate format, then Ax + ATx – diag(A) is returned. If A is banded, then it must be in band symmetric storage mode. See the chapter introduction for a description of band storage modes.
Discussion
The function SP_MVMUL computes a matrix-vector product involving a sparse matrix and a dense vector.
If A is stored in coordinate format, then the arguments nrows, ncols, a, and x should be used. If the keyword Symmetric is set, then Ax + ATx – diag(A) is returned.
If A is a banded, then the arguments nrows, ncols, nlca, nuca, a, and x should be used. If the keyword Symmetric is set, then A must be in band symmetric storage mode, and the number of codiagonals should be used for both nlca and nuca.
Example 1
In this example, Ax is computed where A is stored in coordinate format.
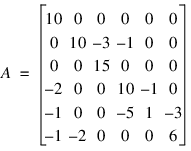
Let: xT = (1, 2, 3, 4, 5, 6)
; Define the sparse matrix A using coordinate storage format.
A = replicate(!F_sp_elem, 15)
a(*).row = [0, 1, 1, 1, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5]
a(*).col = [0, 1, 2, 3, 2, 0, 3, 4, 0, 3, 4, 5, 0, 1, 5]
a(*).val = [10, 10, -3, -1, 15, -2, 10, -1, -1, -5, $
1, -3, -1, -2, 6]
x= [1, 2, 3, 4, 5, 6]]
ax = SP_MVMUL(6, 6, a, x)
PM, ax
; PV-WAVE prints the following:
; 10.000000
; 7.0000000
; 45.000000
; 33.000000
; -34.000000
; 31.000000
Example 2
In this example, Ax is computed where A is stored in band mode. Consider the 1000 × 1000 banded matrix below:
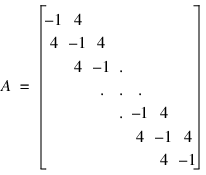
Let x(*) = 2.
n_rows = 1000L
nlca = 1L
nuca = 1L
; Fill A with the values of the bands.
a = DBLARR(n_rows*(nlca+nuca+1))
a(1:n_rows-1) = 4
a(n_rows:2*n_rows-1) = -1
a(2*n_rows:*) = 4
; Fill up x.
x = DBLARR(n_rows)
x(*) = 2
; Define the expected result.
expected = DBLARR(n_rows)
expected(*) = 14
expected(0) = 6
expected(n_rows-1) = 6
; Compute the product, then output the difference between the
; computed result and the expected result.
ax = SP_MVMUL(n_rows, n_rows, nlca, nuca, a, x)
PRINT, TOTAL(ABS(ax-expected)) ; 0.0000000
Example 3
In this example, Ax is computed where A is stored in band symmetric mode. Let:
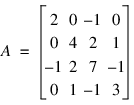 ,
, 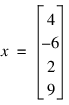
n = 4L
ncoda = 2L
; Fill up contents of A.
a = DBLARR((ncoda+1)*n)
a(0:n-1) = [0, 0, -1, 1]
a(n:2L*n-1) = [0, 0, 2, -1]
a(2L*n:*) = [2, 4, 7, 3]
x = [4, -6, 2, 9]
; Call SP_MVMUL with the keyword Symmetric set.
ax = SP_MVMUL(n, n, ncoda, ncoda, a, x, /Symmetric)
PM, ax
; PV-WAVE prints the following:
; 6.0000000
; -11.000000
; -11.000000
; 19.000000