SP_BDPDSOL Function
Solves a symmetric positive definite system of linear equations Ax = b in band symmetric storage mode. Using keywords, any of several related computations can be performed.
Usage
result = SP_BDPDSOL(b, ncoda[, a])
Input Parameters
b—One-dimensional matrix containing the right-hand side.
ncoda—Number of upper codiagonals in a.
a—(Optional) Array of size (ncoda + 1) × n containing the n × n banded coefficient matrix in band symmetric storage mode A(i, j). See the chapter introduction for a description of band symmetric storage mode.
Returned Value
result—A one-dimensional array containing the solution of the linear system Ax = b.
Input Keywords
Factor—An array of size (ncoda + 1) × N_ELEMENTS(b) containing the RTR factorization of A in band symmetric storage mode, as returned from SP_BDPDFAC.
Double—If present and nonzero, double precision is used.
Output Keywords
Condition—Specifies a named variable into which an estimate of the L1 condition number is stored. This keyword cannot be used if a previously computed factorization is specified with Factor.
Discussion
The function SP_BDPDSOL solves a system of linear algebraic equations with a symmetric positive definite band coefficient matrix A. It computes the RTR Cholesky factorization of A. R is an upper triangular band matrix.
The L1 condition number of A is computed using Higham’s modifications to Hager’s method, as given in Higham (1988). If the estimated condition number is greater than 1/ε (where ε is the machine precision), a warning message is issued. This indicates that very small changes in A may produce large changes in the solution x.
The function SP_BDPDSOL fails if any submatrix of R is not positive definite or if R has a zero diagonal element. These errors occur only if A is very close to a singular matrix or to a matrix which is not positive definite.
The function SP_BDPDSOL is partially based on the LINPACK subroutines CPBFA and SPBSL; see Dongarra et al. (1979).
Example 1
Solve a system of linear equations Ax = b, where:
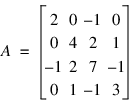 ,
, 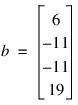
n = 4L
ncoda = 2L
; Define A in band symmetric storage mode.
a = DBLARR((ncoda+1)*n)
a(0:n-1) = [0, 0, -1, 1]
a(n:2L*n-1) = [0, 0, 2, -1]
a(2L*n:*) = [2, 4, 7, 3]
b = [6, -11, -11, 19]
; Compute the solution
x = SP_BDPDSOL(b, ncoda, a)
PM, x ; PV-WAVE prints the following:
; 4.0000000
; -6.0000000
; 2.0000000
; 9.0000000





