Solves a sparse symmetric positive definite system of linear equations Ax = b.

b—One-dimensional matrix containing the right-hand side.

a—(Optional) Sparse matrix stored as an array of structures containing non-zeros in lower triangle of the coefficient matrix A(i,j). See the chapter introduction for a description of structures used for sparse matrices.

result—A one-dimensional array containing the solution of the linear system Ax = b.

Multifrontal—If present and nonzero, perform the numeric factorization using a multifrontal technique. By default a standard factorization is computed based on a sparse compressed storage scheme. Keywords MultiFrontal and Factor cannot be used together.

Factor—The factorization of A as computed by SP_PDFAC. If this keyword is used, then the argument a should not be used. This keyword is useful if solutions to systems involving the same coefficient matrix and multiple right-hand sides will be solved.

Csc_col—Accept the coefficient matrix in compressed sparse column (CSC) format. See the chapter introduction for a discussion of this storage scheme. The keywords Csc_col, Csc_row, and Csc_val must be used together.

Csc_row—Accept the coefficient matrix in compressed sparse column (CSC) format. See the chapter introduction for a discussion of this storage scheme. The keywords Csc_col, Csc_row, and Csc_val must be used together.

Csc_val—Accept the coefficient matrix in compressed sparse column (CSC) format. See the chapter introduction for a discussion of this storage scheme. The keywords Csc_col, Csc_row, and Csc_val must be used together.

Sm_diag—The smallest diagonal element that occurred during the numeric factorization. This keyword is not valid if the keyword Factor is used.

Lg_diag—The largest diagonal element that occurred during the numeric factorization. This keyword is not valid if the keyword Factor is used.

N_nonzero—Specifies a named variable into which the total number of non-zeros in the factor is stored. This keyword is not valid if the keyword Factor is used.

The function SP_PDSOL solves a system of linear algebraic equations having a sparse symmetric positive definite coefficient matrix A. In this function’s default usage, a symbolic factorization of a permutation of the coefficient matrix is computed first. Then a numerical factorization is performed. The solution of the linear system is then found using the numeric factor.

The symbolic factorization step of the computation consists of determining a minimum degree ordering and then setting up a sparse data structure for the Cholesky factor, L. This step only requires the “pattern” of the sparse coefficient matrix, that is, the locations of the non-zero elements but not any of the elements themselves.

The numerical factorization can be carried out in one of two ways. By default, the standard factorization is performed based on a sparse compressed storage scheme. This is fully described in George and Liu (1981). Optionally, a multifrontal technique can be used. The multifrontal method requires more storage but will be faster in certain cases. The multifrontal factorization is based on the routines in Liu (1987). For a detailed description of this method, see Liu (1990), also Duff and Reid (1983, 1984), Ashcraft (1987), Ashcraft et al. (1987), and Liu (1986, 1989).

If an application requires that several linear systems be solved where the coefficient matrix is the same but the right-hand sides change, the function SP_PDFAC can be used to precompute the Cholesky factor. Then the keyword Factor can be used in SP_PDSOL to efficiently solve all subsequent systems.

Given the numeric factorization, the solution x is obtained by the following calculations:

The permutation information, P, is carried in the numeric factor structure.

As an example consider the 5 × 5 coefficient matrix:

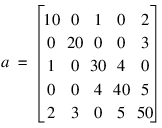
Let xT = (5, 4, 3, 2, 1) so that Ax = (55, 83, 103, 97, 82)T. The number of non-zeros in the lower triangle of A is nz = 10. The sparse coordinate form for the lower triangle is given by:

Since this representation is not unique, an equivalent form would be:

A = REPLICATE(!F_sp_elem, 10) 

a(*).row = [0, 1, 2, 2, 3, 3, 4, 4, 4, 4]

a(*).col = [0, 1, 0, 2, 2, 3, 0, 1, 3, 4]

a(*).val = [10, 20, 1, 30, 4, 40, 2, 3, 5, 50] 

b = [55.0d0, 83, 103, 97, 82] 

x = SP_PDSOL(b, a)

PM, x ; PV-WAVE prints the following:

   ; 5.0000000

   ; 4.0000000

   ; 3.0000000

   ; 2.0000000

   ; 1.0000000