SP_BDFAC Procedure
Computes the LU factorization of a matrix stored in band storage mode.
Usage
SP_BDFAC, nlca, nuca, n_rows, a, pivot, factor
Input Parameters
nlca—Number of lower codiagonals in a.
nuca—Number of upper codiagonals in a.
n_rows—Number of rows in a.
a—Array of size (nlca + nuca + 1) × n containing the n × n banded coefficient matrix in band storage mode A(i,j). See the chapter introduction for a description of band storage mode.
Output Parameters
pivot—One-dimensional array containing the pivot sequence. Keyword Pivot and Condition cannot be used together.
factor—An array of size (2*nlca + nuca + 1) × n_rows containing the LU factorization of A with column pivoting. Keywords Factor and Condition cannot be used together.
Input Keywords
Blk_factor—The blocking factor. This keyword must be set no larger than 32. Default: Blk_factor = 1.
Double—If present and nonzero, double precision is used.
Output Keywords
Condition—Specifies a named variable into which an estimate of the L1 condition number is stored. Keyword Condition cannot be used with parameters pivot or factor.
Discussion
The function SP_BDFAC computes the LU factorization of A with based on the blocked LU factorization algorithm given in Du Croz, et al, (1990). Level-3 BLAS invocations were replaced by in-line loops. The blocking factor Blk_factor has the default value of 1, but can be reset to any positive value not exceeding 32.
An estimate of the L1 condition number of A is computed using Higham’s modifications to Hager’s method, as given in Higham (1988). If the estimated condition number is greater than 1/ε (where ε is the machine precision), a warning message is issued. This indicates that very small changes in A may produce large changes in the solution x.
Example 1
Consider the 1000 × 1000 banded matrix below:
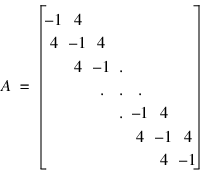
In this example we compute the solution to Ax1 = b1 and Ax2 = b2, where b1 and b2 are random vectors. The factorization is computed just once, using SP_BDFAC, and the solutions are computed using SP_BDSOL.
n_rows = 1000L
nlca = 1L
nuca = 1L
; Fill A with the values of the bands.
a = DBLARR(n_rows*(nlca+nuca+1))
a(1:n_rows-1) = 4
a(n_rows:2*n_rows-1) = -1
a(2*n_rows:*) = 4
seed = 123L
; Fill random vectors
b1 = RANDOMU(seed, n_rows)
b2 = RANDOMU(seed, n_rows)
; Compute the factorization using SP_BDFAC.
SP_BDFAC, nlca, nuca, n_rows, a, pivot, factor
; Compute solution of Ax1 = b1 above, and output residual below.
x1 = SP_BDSOL(b1, nlca, nuca, Factor = factor, Pivot = pivot)
PM, TOTAL(ABS(SP_MVMUL(n_rows, n_rows, nlca, nuca, a, x1)-b1))
; PV-WAVE prints: 1.2367884e-13
; Compute the solution of Ax2 = b2 above, and output residual.
x2 = SP_BDSOL(b2, nlca, nuca, Factor = factor, Pivot = pivot)
PM, TOTAL(ABS(SP_MVMUL(n_rows, n_rows, nlca, nuca, a, x2)-b2))
; PV-WAVE prints: 9.1537888e-14
See Also





