TIME_SERIES_CLASS_FILTER Function
Converts time series data sorted within nominal classes in decreasing chronological order to a useful format for processing by a neural network.
Usage
z = TIME_SERIES_CLASS_FILTER(n_lags, n_classes, i_class, x)
Input Parameters
n_lags—Scalar value indicating the number of lags. The number of lags must be one or greater.
n_classes—Scalar value indicating the number of classes associated with these data. The number of classes must be one or greater.
i_class—Array of length n_obs, where n_obs is the number of observations. The ith element in i_class is equal to the class associated with the ith element of x. The classes must be numbered from 1 to n_classes.
x—Float array of length n_obs. This array is assumed to be sorted first by class designations and then descending by chronological order, i.e., most recent observations appear first within a class.
Returned Value
z—Array of size n_obs by n_lags. The ith column contains the lagged values of x for a lag equal to the number of lags in Lags(i).
Input Keywords
Double—If present and nonzero, double precision is used.
Lags—Array of length n_lags. The ith element in Lags is equal to the lag requested for the ith column of z. Every lag must be non-negative. Default: Lags(i) = i
Discussion
TIME_SERIES_CLASS_FILTER accepts a data array, x, and returns a new data array, z, containing n_lags columns, each containing a lagged version of x.
The output data array, z, can be represented symbolically as:
z = |x(0) : x(1) : x(2) : … : x(n_lags – 1)|
where x(i) is the ith lagged column of the incoming data array, x. Notice that n_lags is the number of lags and not the maximum lag. The maximum number of lags is max_lag = n_lags – 1, unless the Lags keyword is given, the highest lag is max_lags. If n_lags = 2 and the Lags keyword is not given, then the output array contains the lags 0, 1.
Consider, an example in which n_obs = 10, n_lags = 2 and:
xT = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
If lagT = {0, 2} and:
i_classT = {1, 1, 1, 1, 1, 1, 1, 1, 1, 1}
then, n_classes = 1 and z would contain 2 columns and 10 rows:

Note that since lagT = [0,1], the first column of z is formed using a lag of zero and the second is formed using a lag of two. A zero lag corresponds to no lag, which is why the first column of z in this example is equal to the original data in x.
On the other hand, if the data were organized into two classes with:
i_classT = {1, 1, 1, 1, 1, 2, 2, 2, 2, 2}
then z is still a 2 by 10 matrix, but with the following values:
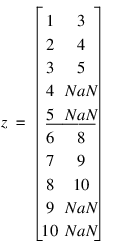
The first 5 rows of z are the lagged columns for the first class, and the last five are the lagged columns for the second class.
Example
Suppose that the training data to the neural network consists of the following data matrix consisting of a single nominal variable coded into two binary columns and a single time series variable:
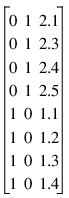
In this case, n_obs = 8 and n_classes = 2. If we wanted to lag the 3rd column by 2 time lags, i.e., n_lags=2:
lagT = {0,1}
i_classT = {1,1,1,1,2,2,2,2}
xT = {2.1,2.3,2.4,2.5,1.1,1.2,1.3,1,4}
The resulting data matrix would have 4 rows and 2 columns:
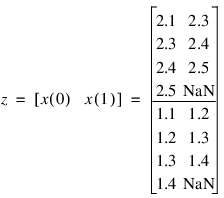
; Input data X is 1-D array of length n_obs
; Result array is a 2-D array of length n_obs x n_lags
a = MACHINE(/Float)
NaN = a.NAN
; Input. The number of lags
n_lags = 2
; An array of length n_obs
x = [2.1, 2.3, 2.4, 2.5, 1.1, 1.2, 1.3, 1.4]
; The number of classes associated with these data.
n_classes = 2;
; An array of length n_obs.
i_class = [1,1,1,1,2,2,2,2]
z = TIME_SERIES_CLASS_FILTER(n_lags, n_classes, i_class, x)
PRINT, ""
PM, Z, Title ="Z"
Output
Z
2.10000 2.30000
2.30000 2.40000
2.40000 2.50000
2.50000 NaN
1.10000 1.20000
1.20000 1.30000
1.30000 1.40000
1.40000 NaN





