RANDOM_ARMA Function
Generates a time series from a specific ARMA model.
Usage
result = RANDOM_ARMA(n, nparams)
result = RANDOM_ARMA(n, nparams, ar)
result = RANDOM_ARMA(n, nparams, ma)
result = RANDOM_ARMA(n, nparams, ar, ma)
Input Parameters
n—Number of observations to be generated. Parameter n must be greater than or equal to one.
nparams—One-dimensional array containing the parameters p and q consecutively. nparams(0) = p, where p is the number of autoregressive parameters. Parameter p must be greater than or equal to zero. nparams(1) = q, where q is the number of moving average parameters. Parameter q must be greater than or equal to zero.
ar—One-dimensional array of length p containing the autoregressive parameters.
ma—One-dimensional array of length q containing the moving average parameters.
Returned Value
result—One-dimensional array of length n containing the generated time series.
Input Keywords
Double—If present and nonzero, double precision is used.
Const—Overall constant. See the Discussion section. Default: Const = 0
Var_Noise—If present (and Input_Noise is not used), noise at is generated from a normal distribution with mean 0 and variance Var_Noise. Var_Noise and Input_Noise cannot be used together. Default: Var_Noise = 1.0
Input_Noise—One-dimensional array of length n + max (Ar_Lags(i)) containing the random noises. Keywords Input_Noise and Var_Noise can not be used together. Keywords Input_Noise and Output_Noise cannot be used together.
Ar_Lags—One-dimensional array of length p containing the order of the nonzero autoregressive parameters. Default: Ar_Lags = [1, 2, ..., p]
Ma_Lags—One-dimensional array of length q containing the order of the nonzero moving average parameters. Default: Ma_Lags = [1, 2, ..., q]
W_Init—One-dimensional array of length max (Ar_Lags(i)) containing the initial values of the time series. Default: W_Init(*) = Const/(1 – ar(0) – ar(1) – ... – ar(p − 1))
Accept_Reject—If present and nonzero, the random noises will be generated from a normal distribution using an acceptance/rejection method. If keyword Accept_Reject is not used, the random noises will be generated using an inverse normal CDF method. This argument will be ignored if keyword Input_Noise is used.
Output Keywords
Output_Noise—Named variable into which a one-dimensional array of length n + max (Ma_Lags(i)) containing the random noises is stored.
Discussion
Function RANDOM_ARMA simulates an ARMA(p, q) process, {Wt}, for t = 1, 2, ..., n. The model is:
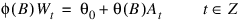
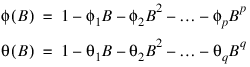
Let μ be the mean of the time series {Wt}. The overall constant θ0 (Const) is:
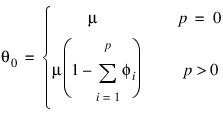
Time series whose innovations have a nonnormal distribution may be simulated by providing the appropriate innovations in Input_Noise and start values in W_Init.
The time series is generated according to the following model:
X(i) = Const + ar(0) * X(i – Ar_Lags(0)) + ... + ar(p – 1) * X(i – Ar_Lags(p – 1)) +
A(I) – ma(0) * A(i – Ma_Lags(0)) – ... – ma(q – 1) * A(i – Ma_Lags(q – 1))
where the constant is related to the mean of the series:
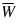
as follows:
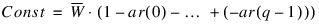
and where:
X(t) = W(t), t = 0, 1, ..., n − 1
and:
W(t) = W_Init(t + p), t = –p, –p + 1, ..., −2,−1
and A is either Input_Noise (if Input_Noise is used) or Output_Noise (otherwise).
Example 1
In this example, RANDOM_ARMA is used to generate a time series of length five, using an ARMA model with three autoregressive parameters and two moving average parameters. The start values are 0.1000, 0.0500, and 0.0375.
RANDOMOPT, set = 123457
n = 5
nparams = [3, 2]
ar = [0.5, 0.25, 0.125]
ma = [-0.5, -0.25]
r = RANDOM_ARMA(n, nparams, ar, ma)
PM, r, Format = '(5F10.3)',$
Title = ' ARMA random deviates'
; PV-WAVE prints the following:
; ARMA random deviates
; 0.637 0.317 -0.366 -2.122 -1.407
Example 2
In this example, a time series of length 5 is generated using an ARMA model with 4 autoregressive parameters and 2 moving average parameters. The start values are 0.1, 0.05 and 0.0375.
RANDOMOPT, set = 123457
n = 5
nparams = [3, 2]
ar = [0.5, 0.25, 0.125]
ma = [-0.5, -0.25]
wi = [0.1, 0.05, 0.0375]
theta0 = 1
avar = 0.1
r = RANDOM_ARMA(n, nparams, ar, ma, /Accept_Reject, $
W_Init = wi, Const = theta0, Var_Noise = avar)
PM, r, Format = '(5F10.3)', $
Title = ' ARMA random deviates:'
; PV-WAVE prints the following:
; ARMA random deviates:
; 1.467 1.788 2.459 3.330 3.941
Warning Errors
STAT_RNARM_NEG_VAR—VAR(a) = “Var_Noise” = #, VAR(a) must be greater than 0. The absolute value of # is used for VAR(a).





