Introduction
The Random Numbers section describes functions for the generation of random numbers that are useful for applications in Monte Carlo or simulation studies. Before using any of the random number generators, the generator must be initialized by selecting a seed or starting value. The user can do this by calling the function RANDOMOPT. If the user does not select a seed, one is generated using the system clock. A seed needs to be selected only once in a program, unless two or more separate streams of random numbers are maintained. Utility functions in this chapter can be used to select the form of the basic generator to restart simulations and to maintain separate simulation streams.
In the following discussions, the phrases “random numbers,” “random deviates,” “deviates,” and “variates” are used interchangeably. The phrase “pseudorandom” is sometimes used to emphasize that the numbers generated are really not “random” since they result from a deterministic process. The usefulness of pseudorandom numbers is derived from the similarity, in a statistical sense, of samples of the pseudorandom numbers to samples of observations from the specified distributions. In short, while the pseudorandom numbers are completely deterministic and repeatable, they simulate the realizations of independent and identically distributed random variables.
Basic Uniform Generator
The default action of the RANDOM function is the generation of uniform (0,1) numbers. This function is portable in the sense that, given the same seed, it produces the same sequence in all computer/compiler environments.
The random number generators in this chapter use either a multiplicative congruential method or a generalized feedback shift register (GFSR) method. The selection of the type of generator is made by calling the RANDOMOPT Procedure. If no selection is made explicitly, a multiplicative generator (with multiplier 16807) is used. Whatever distribution is being simulated, uniform (0, 1) numbers are first generated and then transformed if necessary. These routines are portable in the sense that, given the same seed and for a given type of generator, they produce the same sequence in all computer/compiler environments. There are many other issues that must be considered in developing programs for the methods described below (see Gentle 1981 and 1990).
Multiplicative Congruential Generators
The form of the multiplicative congruential generators is:
xi ≡ cxi-1mod (231 - 1)
Each xi is then scaled into the unit interval (0,1). If the multiplier, c, is a primitive root modulo 231 - 1 (which is a prime), then the generator will have a maximal period of 231 - 2. There are several other considerations, however. See Knuth (1981) for a good general discussion. The possible values for c in the generators are 16807, 397204094, and 950706376. The selection is made by the function RANDOMOPT. The choice of 16807 will result in the fastest execution time, but other evidence suggests that the performance of 950706376 is best among these three choices (Fishman and Moore 1982). If no selection is made explicitly, the functions use the multiplier 16807, which has been in use for some time (Lewis et al. 1969).
Shuffled Generators
The user also can select a shuffled version of these generators using RANDOMOPT. The shuffled generators use a scheme due to Learmonth and Lewis (1973). In this scheme, a table is filled with the first 128 uniform (0,1) numbers resulting from the simple multiplicative congruential generator. Then, for each xi from the simple generator, the low-order bits of xi are used to select a random integer, j, from 1 to 128. The jth entry in the table is then delivered as the random number; and xi, after being scaled into the unit interval, is inserted into the jth position in the table. This scheme is similar to that of Bays and Durham (1976), and their analysis is applicable to this scheme as well.
Generalized Feedback Shift Register Generator
The GFSR generator uses the recursion 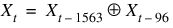 . This generator, which is different from earlier GFSR generators, was proposed by Fushimi (1990), who discusses the theory behind the generator and reports on several empirical tests of it. Background discussions on this type of generator can be found in Kennedy and Gentle (1980), pages 150-162.
. This generator, which is different from earlier GFSR generators, was proposed by Fushimi (1990), who discusses the theory behind the generator and reports on several empirical tests of it. Background discussions on this type of generator can be found in Kennedy and Gentle (1980), pages 150-162.
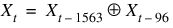 . This generator, which is different from earlier GFSR generators, was proposed by Fushimi (1990), who discusses the theory behind the generator and reports on several empirical tests of it. Background discussions on this type of generator can be found in Kennedy and Gentle (1980), pages 150-162.
. This generator, which is different from earlier GFSR generators, was proposed by Fushimi (1990), who discusses the theory behind the generator and reports on several empirical tests of it. Background discussions on this type of generator can be found in Kennedy and Gentle (1980), pages 150-162.Setting Seed
The seed of the generator can be set and retrieved using RANDOMOPT. Prior to invoking any generator in this section, the user can call RANDOMOPT to initialize the seed, which is an integer variable with a value between 1 and 2147483647. If it is not initialized by RANDOMOPT, a random seed is obtained from the system clock. Once it is initialized, the seed need not be set again.
If the user wants to restart a simulation, RANDOMOPT can be used to obtain the final seed value of one run to be used as the starting value in a subsequent run. Also, if two simultaneous random number streams are desired in one run, RANDOMOPT can be used before and after the invocations of the generators in each stream.
If a shuffled generator or the GFSR generator is used, in addition to resetting the seed, the user must also reset some values in a table. For the shuffled generators, this is done using the routine RANDOM_TABLE. The tables for the shuffled generators are separate for single and double precision; so, if precisions are mixed in a program, it is necessary to manage each precision separately for the shuffled generators.
Timing Considerations
The generation of the uniform (0,1) numbers is done by RANDOM. The particular generator selected in RANDOMOPT, that is, the value of the multiplier and whether shuffling is done or whether the GFSR generator is used, affects the speed of RANDOM. The smaller multiplier (16807, selected by Gen_option = 1 or Gen_option = 2) is faster than the other multipliers. The multiplicative congruential generators that do not shuffle are faster than the ones that do. The GFSR generator is roughly as fast as the fastest multiplicative congruential generator, but the initialization for it (required only on the first invocation) takes longer than the generation of thousands of uniform random numbers. Precise statements of relative speeds depend on the computing system.
Distributions Other than Uniform
The nonuniform generators use a variety of transformation procedures. All of the transformations used are exact (mathematically). The most straightforward transformation is the inverse CDF technique, but it is often less efficient than others involving acceptance/rejection and mixtures. See Kennedy and Gentle (1980) for discussion of these and other techniques.
Many of the nonuniform generators in this chapter use different algorithms depending on the values of the parameters of the distributions. This is particularly true of the generators for discrete distributions. Schmeiser (1983) gives an overview of techniques for generating deviates from discrete distributions.
Although, as noted above, the uniform generators yield the same sequences on different computers, because of rounding, the nonuniform generators that use acceptance/rejection may occasionally produce different sequences on different computer/compiler environments.
Although the generators for nonuniform distributions use fast algorithms, if a very large number of deviates from a fixed distribution are to be generated, it might be worthwhile to consider a table sampling method, as implemented in the routines RAND_GEN_CONT and RAND_GEN_DISCR.
Tests
Extensive empirical tests of some of the uniform random number generators available in RANDOM are reported by Fishman and Moore (1982 and 1986). Results of tests on the generator using the multiplier 16807 with and without shuffling are reported by Learmonth and Lewis (1973b). If the user wishes to perform additional tests, the routines in Chapter 8: Goodness of Fit may be of use. Often in Monte Carlo applications, it is appropriate to construct an ad hoc test that is sensitive to departures that are important in the given application. For example, in using Monte Carlo methods to evaluate a one-dimensional integral, autocorrelations of order one may not be harmful, but they may be disastrous in evaluating a two dimensional integral. Although generally the routines in this chapter for generating random deviates from nonuniform distributions use exact methods, and, hence, their quality depends almost solely on the quality of the underlying uniform generator, it is often advisable to employ an ad hoc test of goodness of fit for the transformations that are to be applied to the deviates from the nonuniform generator.
Additional Notes on Usage
The generators for continuous distributions are available in both single and double precision versions. This is merely for the convenience of the user; the double precision versions should not be considered more “accurate,” except possibly for the multivariate distributions.





