BINOMIALPDF Function
Evaluates the binomial probability function.
Usage
result = BINOMIALPDF (k, n, p)
Input Parameters
k—Argument for which the binomial probability function is to be evaluated.
n—Number of Bernoulli trials.
p—Probability of success on each trial.
Returned Value
result—The probability that a binomial random variable takes a value equal to k.
Discussion
The function BINOMIALPDF evaluates the probability that a binomial random variable with parameters n and p takes on the value k. It does this by computing probabilities of the random variable taking on the values in its range less than (or the values greater than) k. These probabilities are computed by the recursive relationship:
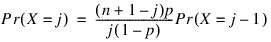
To avoid the possibility of underflow, the probabilities are computed forward from 0, if k is not greater than n times p, and are computed backward from n, otherwise. The smallest positive machine number, ε, is used as the starting value for computing the probabilities, which are rescaled by (1 - p)nε if forward computation is performed and by pnε if backward computation is done.
For the special case of p = 0, BINOMIALPDF returns 0 if k is greater than 0 and to 1 otherwise; and for the case p = 1, BINOMIALPDF returns 0 if k is less than n and to 1 otherwise.
Example
Suppose X is a binomial random variable with n = 5 and p = 0.95. In this example, we find the probability that X is equal to 3.
PRINT, BINOMIALPDF(3, 5, .95)
; PV-WAVE prints: 0.0214344





